探究小學生運算能力的培養

文/廣州市海珠區大元帥府小學 洪 虹

運算能力是學生在進行課程學習中應具備的數學核心素養之一，它是促進學生發展的重要方面。在《義務教育數學課程標準 （2011年版）》中指出： “運算能力主要是指能夠根據法則和運算律正確地進行運算的能力。培養運算能力有助于學生理解運算的算理，需求合理簡潔的運算途徑解決問題。”由此可見，判斷一個學生的運算能力如何，不僅僅看他是否運算正確，還要看他對算理的理解，以及是否會選擇合理簡潔的運算途徑。下面以《異分母分數加減法》為例，對小學生運算能力的培養進行探討。

【片段三】下面檢查一下自己對這節課的內容是否真的懂，有信心嗎？看圖填空。

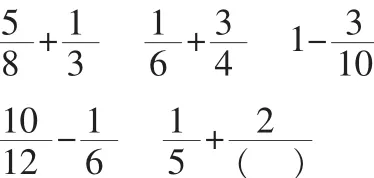
一、借多元表征理解算理，培養運算能力

在計算教學的前測中，普遍存在有部分學生知道怎樣做，但沒幾個知道為什么可以這樣做，說明了算理既是計算教學的重點，也是難點。如何讓學生對 “算理”這個新知識的理解，根據布魯納和萊什的表征理論，可以借用表征進行數學學習，有助于提升學生學習的深度和廣度。在片段一中，教師引導學生進行了兩個層次的學習。先是學生自主運用多元表征初悟算理，如動作表征、語義表征、符號表征。學生不同的思維方式會選擇不同的表征，但要多角度去深入理解，還需要教師適時介入，幫助學生會轉化各種表征，并在不同的表征之間建立廣泛的聯系。因此展開了更深層次的學習，啟發學生溝通不同表征深悟算理。例如，通過設問 “有沒有同學把通分這種思路用等式表示出來”，引導用了語義表征的學生學會用符號表征。又例如通過追問 “如果不拼，怎樣在圖中畫一畫，讓大家看到”，數形結合幫助學生溝通算理算法，以達到循“理” 入 “法”，以 “理”馭 “法”。最后通過反思 “這些方法有什么共同的地方”，有效溝通了整數、小數、同分母分數加減法都是 “相同單位的數才能相加、減”這一內在算理，初步形成知識鏈，培養學生的運算能力。

二、借自我體驗合理選擇，培養運算能力

建構主義認為世界是客觀存在的，但是對于世界的理解和賦予意義卻是由每個人自己決定的，因此學習不是由教師把知識簡單地傳遞給學生，而是由學生自己建構知識的過程。在探索計算方法的過程中，學生根據自己的思維方式呈現了多種算法，其中 “通分”的方法具有普適性，但如果要求學生生搬硬造統一用 “通分”法，學生不僅被動接受知識，打擊學習積極性，還會影響對知識的理解。片段二中，教師設計了 “用你喜歡的方法來計算的學習情境，讓學生在活動中對自己 “創造”的方法進行判斷、選擇，從而體驗出把分數化成小數或折紙、畫圖等方法的局限性，感受到 “先通分，再計算”的普適性。再通過教師的追問 “剛才你們想到了那么多種方法，為什么都用通分的方法來計算”，推動學生再次回顧從 “尋求”到 “合理簡潔”的 “運算途徑”，從而培養學生的運算能力。

三、借分層內化促進正確，培養運算能力

有效的練習能提高學生運算的正確率。在片段三中，教師設計的“看圖填空”，利用數形結合，通過在反饋時的追問 “用了什么知識？為什么？”，促使學生對異分母分數加減法 “先通分再計算”道理的再次理解，為正確計算打好基礎。第二題的五道計算，既有新知，又有舊知。在反饋時，教師的設問 “在三年級計算1減幾分之幾時，我們都是根據減數的分母把1化成相應的分數，這實際上是用了什么知識”，幫助學生進行知識的同化。在反饋時，通過追問 “除了用通分的知識，還有沒有其他的知識來解決”，讓學生知道要使計數單位相同，不一定通分，特殊情況還可以約分，這主要是考慮到以后的混合運算中有可能會出現這種情況，培養學生靈活運用知識解決問題的能力。是開放性題目，目的再次強調同分母分數和異分母分數加減法算法上的區別。這五道計算題各有各的功能，幫助學生對算法的內化，滲透計算技巧，為正確計算夯實基礎，從而培養學生的運算能力。