一道題，一節課

楊伊

習題是數學教材的重要組成部分，常常起著鞏固知新、技能形成、訓練思維等功能，因而，習題教學是課堂教學不可忽視的環節。但我在聽課時發現一些教師在教習題時，由于缺乏應有的思考和必要的專業知識，常常是過程簡單、方法單一，導致習題教學效果不佳。

我們來看一道習題的教學。人教版數學教材六年級上冊中練習二十三第16題（如圖1所示），我看過多個不同班級的孩子解答此題時都只用了一種最基本且計算最復雜的方法，詢問授課老師解決這個問題是否有簡便的方法，得到的回答都是否定的。而我在教學這道題的時候幾乎花了一節課的時間，學生不但得出了多種解題方法，而且在整個探究過程中勁頭十足，很有成就感。其教學過程簡單記錄如下。

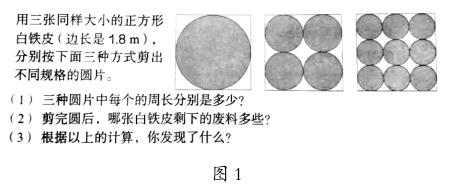
第一小題是基礎題，教師讓學生先動筆做。學生的方法基本都是：第一種圓片的周長是3.14×1.8=5.652（m），第二種圓片的周長是3.14×（1.8÷2）=2.826（m），第三種圓片的周長是3.14×（1.8÷3）=1.884（m）。

教師引導學生觀察每種規格圓的直徑之間的關系，以及與大圓周長之間的關系。學生馬上想到了第二種方法：第一種圓片的周長是3.14×1.8=5.652（m）；第二種圓片的周長是5.652÷2=2.826（m）；第三種圓片的周長是5.652÷3=1.884（m）。

當學生匯報完后，教師讓學生閉上眼睛聯想：接下來的第四個圖，第五個圖……是什么樣？那些小圓片的周長分別是多少？你發現了什么？這樣既培養了學生的空間想象能力，又將第三小題分成兩部分歸納總結，降低了總結、歸納和表達的難度，讓學生更愿意說。

對于第二小題，教師提議學生先猜想剪完圓后哪一張白鐵皮剩下的廢料多些，能不能用自己的方法來證明。學生分組合作探究后，依次分享了如下的做法。

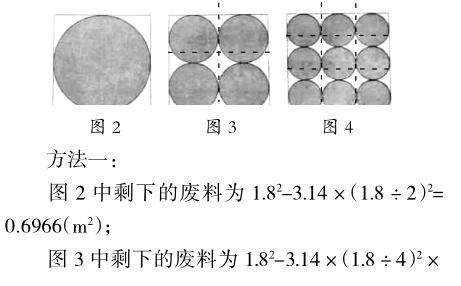
教師問學生：“他的方法對嗎？”學生們紛紛點頭，說：“對，不做這題幾乎忘了外方內圓的知識，真是溫故而知新啊！”這個時候教師還是淡淡地說：“請與這兩種解法不同的同學舉手。”于是教師讓一學生分享了方法三：圖2中圓的半徑是圖3中圓半徑的2倍，所以圖2中圓的面積是圖3中圓面積的4倍，那么圖3中4個圓的總面積就和圖2中圓的面積相等。同理可得圖4中9個圓的總面積和圖2中圓的面積相等，所以三個圖中的陰影部分面積相等，所剩的廢料也相等。

這位學生的話音剛落，其他學生的表現各異，有的瞪大眼睛，恍然大悟：“原來還可以這樣思考！”有的拍著桌子懊惱地說：“天啦，還可以這樣做，我算得手都疼了，嗚……”看著這場景，教師得意地笑了：“是啊，還可以這樣做，你們再動筆算算第四個圖，第五個圖……看剩下的廢料是多少。”學生紛紛說：“后面的圖剩下的廢料和前面的一樣多。”教師順勢問道：“都不用算就知道答案了？你發現了什么？”接下來，學生通過思考、交流，在教師的引導下，將比較的方法準確、完整地表達出來。整節課學生在探究與相互傾聽中，博采眾長，相互完善，體驗到思考的快樂和“說”數學的輕松。

數學教學中，教師要重視對課本習題進行適當的研究，最大限度地發揮習題的功能。這樣做有利于學生開闊視野，學會思考，培養思維的靈活性。（作者單位：湘陰縣教師進修學校）