化歸思想在全國卷立體幾何題中的應用研究

福建省石獅市第一中學 (362700)

莫偉昌

化歸與轉化思想,是高中課標所要求掌握的七大思想之一.實際上,不止在高中階段,數學的公理化思想,本質就是化歸轉化思想.其重要性不言而喻.而在高考題中,一些問題通過轉化,可使問題較容易地解決,特別是某些壓軸題中,也只有使用化歸思想方能解決.本文就化歸思想在近年立體幾何試題中的應用作一探究.

1.在三視圖問題中的應用

從三視圖的來源可知,每組三視圖,都是該幾何體在一個長方體內的投影.所以,三視圖的還原,往往可以轉化到相應的長方體來解決.

例1 (2014全國高考Ⅰ卷,理12)如圖1，網格紙上小正方形的邊長為1，粗實線畫出的是某多面體的三視圖，則該多面體的各條棱中，最長的棱的長度為( ).

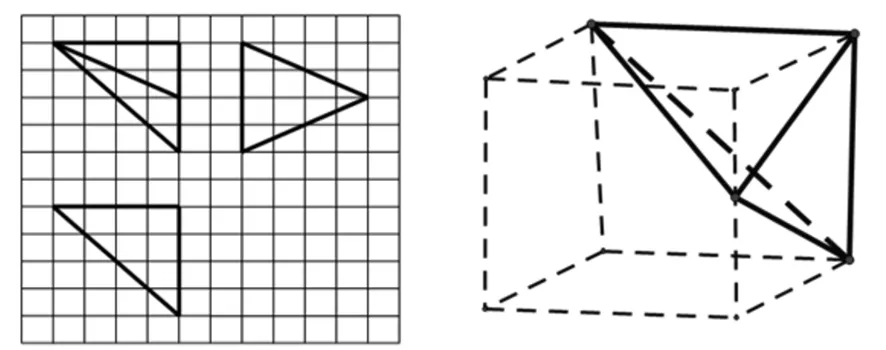
圖1 圖2

分析：作為理科選擇題的壓軸題,直接靠想象就得到比較準確的直觀圖,是很困難的.但如果轉化到一個正方體去分析,可以比較容易得到該幾何體為三棱錐(圖2),而且利用正方體中的垂直關系可以快速地算出相應的棱長,進而選出正確的答案C.當然,如何在正方體中,快速用排除法選出幾何體的頂點,是需要訓練的.

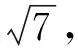
圖3

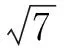
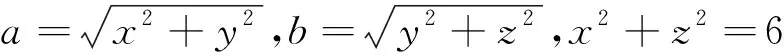
如何轉化到長方體內來做？需要學生在理解三視圖的本質上，有意識地從化歸轉化的角度去思維．

2.在外接球問題上的應用

化歸就是要轉化到已解決的問題，那么外接球已解決的問題是什么？主要是，長方體和直三棱柱的外接球問題．長方體外接球的球心就是長方體的中心，即體對角線的中點．而直三棱柱的外接球球心，就是兩底面外心連線的中點．

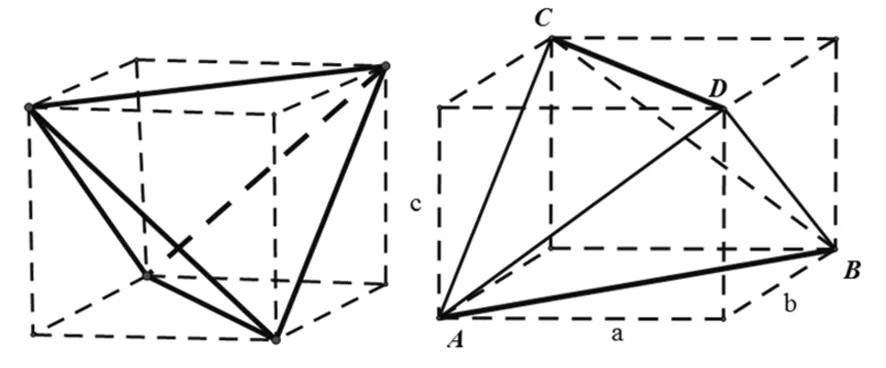
圖4 圖5

例4 (2010年全國高考大綱卷，理12)已知在半徑為2的球面上有A、B、C、D四點，若AB=CD=2,則四面體ABCD的體積的最大值為( ).

分析：若正面去做，比較難以找到入手點．但若能抓住AB=CD，這個關鍵條件，轉化到長方體去分析，問題則迎刃而解．

小結：能轉化到長方體來解決的外接球問題，有兩類，一類是有線面垂直關系的；第二類就是有三對對邊相等的．

3.在夾角問題中應用

兩直線平行,則這兩直線與同一直線或平面的夾角是相等的.所以直線與其他線或面的夾角,可以轉化到其平行線來求.

例5 (2016全國高考Ⅰ卷,理11)平面α過正方體ABCD-A1B1C1D1的頂點A，α∥平面CB1D1，α∩平面ABCD=m，α∩平面ABB1A1=n，則m，n所成角的正弦值為( ).

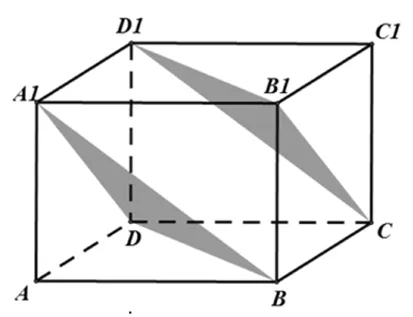
圖6

分析:由已知得,平面α是確定的,但顯然比較難畫出來,即便畫出來,與另外兩個平面的交線m和n也不好畫.故而轉化到找m和n的平行線來做.

如圖6，易得平面A1BD

遇到難題時，懂得轉化到其他已經解決的問題來做，這是意識的問題，通過較長時間的培養即可形成．而轉化到何種問題來解，則是能力問題，它包含了問題本質的識別以及常用方法的應用這個兩個過程，體現了數學抽象、直觀想象和邏輯推理等核心素養．該能力的提升，需要教師精心的選題、思路的啟發和方法的提煉，也需要學生適量的練習、不停的感悟和不斷的總結，缺一不可．