兒童數學抽象力形成的教學分析與提升策略
孫欣 王乃濤

【摘 要】數學抽象力是兒童數學學習的必備品質。兒童的數學抽象學習具有表達直接性、表征直觀性、原理探究性、思維半邏輯性等特點,教師應注重建構有助于提升兒童數學抽象力的適性場域——匹配抽象內容的適應場、激活抽象方法的運用場、提升高階思維的層次場。
【關鍵詞】數學抽象力;教學分析;提升策略;抽象內容;抽象方法;高階思維
【中圖分類號】G623.5? 【文獻標志碼】A? 【文章編號】1005-6009(2019)89-0033-04
【作者簡介】1.孫欣,江蘇省淮陰師范學院第一附屬小學(江蘇淮安,223001)課程教學部副主任,一級教師,淮安市數學學科帶頭人;2.王乃濤,江蘇省淮安經濟技術開發區教師發展中心(江蘇淮安,223005)數學教研員,高級教師,江蘇省數學特級教師。
史寧中教授曾指出:人的基本思維能力就是想象能力和抽象能力,其他思維能力都是它們派生的。數學抽象最能體現數學本質。
一、兒童數學抽象力形成的困惑
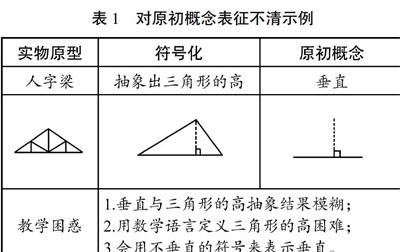
(一)對原初概念表征不清,抽象過程缺少思維基礎
我們通常用已知概念(原初概念)來定義新概念,如用因數來定義質數、合數,用自然數來定義因數。學生對原初概念的理解直接影響他們的新概念形成。如學習蘇教版四下《三角形的高》一課時,由于學生對原初概念的表征與理解不清,往往會致使其新概念抽象過程模糊(如表1)。
(二)對問題解決機械模仿,抽象方法選擇運用不當
教師常結合生活情境來幫助學生理解數學問題,以培養他們用數學的眼光觀察生活的能力。但是,如果教學浮于表面,學生則會對方法理解不透、運用不當。如學習蘇教版一下《100以內加減法》一課時,常常會出現如下頁表2所示的問題。兩道題題型相同,正確率卻相差較大。題1找回錢數很少,符合生活中找回錢少的現實暗示,學生會根據數據特點機械模仿解決題1的方法來解決題2。
(三)對數學原理表達不清,抽象結論難以語義說明
學數學需探究數學原理。建構數學原理時,可舉例、歸納、概括,也可以純數學邏輯推導。受認知能力限制,學生表達數學原理時往往會出現不全面、不完整、不準確等情況。如教學蘇教版五下《分數的基本性質》一課,在折紙、填等式、發現分子分母倍數關系等環節,學生能輕松應對,但讓他們用語言概括規律時,他們的表達卻往往不如人意,有的只表達出了乘或除中的一種情況,有的考慮不到0除外。
(四)對數學本質把握不準,核心要素難以深刻辨析
同一對象可用不同標準進行分類。同一概念處于不同上位概念之下,也以不同樹狀結構引發下位概念。學生對交叉狀的概念體系結構往往難以辨別。如教學蘇教版五下《因數與倍數》一課,不等于0的自然數可分為1、質數和合數,也可分為奇數和偶數。但因學生對數學概念的核心要素把握不準,導致他們對兩種分類標準(是否2的倍數,因數有多少)和概念結構難以深入辨析。
二、兒童數學抽象力的含義及學習特征
(一)兒童數學抽象力的含義
數學抽象力是在數學抽象過程中形成的理解力、判斷力、想象力、概括力等能力的總和。
(二)兒童數學抽象學習的典型特征
小學生的數學抽象主要指情境性抽象或經驗性抽象,具有兩重性,既表示從情境中提取的過程,又表示從過程中得出的經驗概念。
1.表達的直接性。兒童頭腦中的信息屬于“自然結構”,加工起來相對困難,難以進行數學邏輯解釋,而是一點一點地直接表達想法。
2.表征的直觀性。兒童表征數學概念從實物、圖形開始,尚不能完全脫離數學原型展開邏輯思考,抽象過程以具體形象和表象為支撐。
3.原理的探究性。兒童不滿足于接受現有的結論,喜歡從數學事實出發猜想、追問、尋找數學規律,具有一定的探究意識與能力。
4.思維的半邏輯性。兒童抽象能力的發展介于實物、圖形的形象認知和原理、規律的抽象過程之間,具有一定的但不完全的邏輯性,我們稱為“半邏輯性”的學習特點。
三、兒童數學抽象力的培養策略
(一)全面打破——匹配抽象內容的適應場
數學抽象主要有概念抽象、規律抽象、運算抽象、關系抽象、思想方法抽象等。
1.概念抽象——去異求同,抽離本質屬性。要促進學生建立數學概念,教師應注重引導學生觀察、比較,區別事物的本質屬性與非本質屬性,發現事物間共同的屬性,形成正確的概念。如教學蘇教版二下《認識角》一課,可出示實物圖片,引導學生描出圖片中的角,從實物圖中剝離出角的平面圖形,再通過觀察、比較抽象出平面圖形的共同特點,抽離出角的本質屬性(由一個頂點和兩條邊組成)。
2.規律抽象——去粗取精,概括臨近結論。在規律探究中,學生根據研究素材形成的發現有些無普適性。教師應引導學生去除外在表象,展示本質,在臨近結論的基礎上形成正確的結論。如教學蘇教版四下《多邊形內角和》一課,學生通過量、算、拼等方法得出了三角形與四邊形的內角和及2倍關系,但還不能發現邊數與內角和的關系。教師適時啟發:想象一下,多邊形的內角和會與什么有關?當學生理解了多邊形內角和與三角形內角和有關時,就容易找到研究五、六邊形內角和的方法了。借助圖形直觀進行歸納推理,解釋規律的合理性,有助于學生矯正其臨近結論。
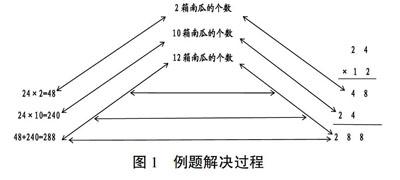
3.運算抽象——理法相通,提煉運算法則。在計算教學中,溝通算理與算法很重要。算理是算法的基礎,及時溝通算法與算理的聯系有利于算法的抽象、提煉與掌握。如蘇教版三下《兩位數乘兩位數的筆算》一課的例題為:幼兒園購進12箱迷你南瓜,每箱24個。一共有多少個?教師教學時應注意引導學生理解算理和豎式過程(如圖1),溝通新舊方法,并啟發學生討論:(1)豎式中第二步算出的積的末位為什么要與十位對齊?(2)新算法為什么要分步表示過程?在數學問題情境中溝通新舊方法,理解算理,抽象出運算法則。

