拋物線內接三角形的面積

山東省萊蕪市教學研究室 (271100) 房增軍

對于坐標系內某一個具體的三角形的面積，我們有很多方法可以求得，但對于無法確定形狀的三角形，其面積求法很難統一起來．經過推導，拋物線內接三角形的面積滿足統一的表達式，現分享給大家，有不正確的地方，請指正．

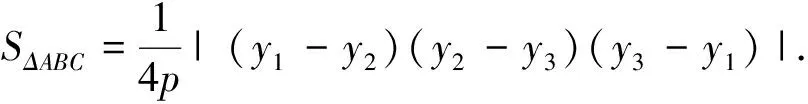
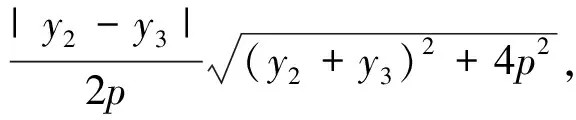
注：如果A、B、C三點中有兩點關于x軸對稱，易知上述公式也成立.

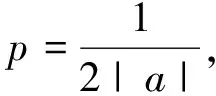
對于拋物線的內接三角形的面積，還有一個重要的結論．

已知A、B、C是拋物線y2=2px(p>0)上三點，過A、B、C三點的拋物線的切線分別交于P、Q、R三點，則SΔABC=2SΔPQR.

圖1

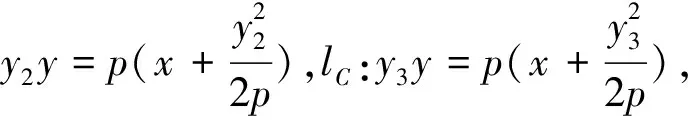
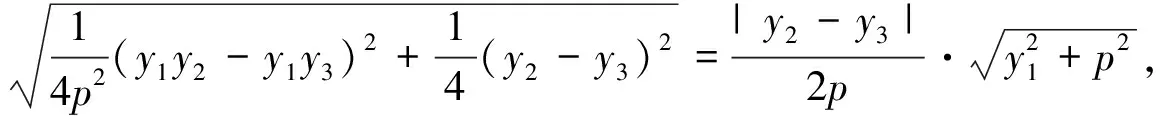
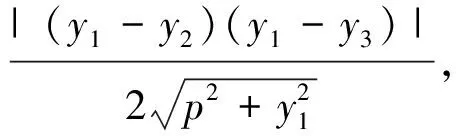
注：如果A、B、C三點中有一點與原點重合，易知上述公式也成立.

∴根據前面的公式，可得SΔABC=2SΔPQR.

在圓錐曲線中，拋物線具有重要地位，它有很多很重要的性質.拋物線方程結構簡單、代數計算量適中，并且關于拋物線的試題具有良好的區分度.結合初中學過的二次函數，對于進一步理解拋物線很有幫助，研究拋物線的相關性質，掌握這些性質對于其它圓錐曲線的學習有很好的借鑒意義.