采用皮亞諾公理證明哥德巴赫猜想
山西省陽泉市晉東化工廠 趙發耀
長春師范大學 王一洲
皮亞諾公理第五條表述如下:任意關于自然數的命題,如果證明了它對自然數0是對的,又假定它對自然數P為真時,可以證明它對P′也真,那么,命題對所有自然數為真[注1]。
一、“研究一文”證明“猜想”成立之公式
經采樣、使用創新的坐標系作圖(本文圖形略)、分析、推導和驗證等步驟,總結出證明“猜想”成立之方程組(下稱“原方程組”)為:

二、采用皮亞諾第五條公理證明“猜想”
“原方程組”(1)式-(2)式經整理得:

(一)證明1:P=0

∵式中y=6,∴n取值只能為0,計算結果得到兩質數:a=3和b=3。
∴證明1正確。
(二)證明2:P=P′(P′為大于0的自然數)
當P=P′時,y=2P′+6,則有:
∵式中y=2P′+6,∴n取值為0~/2范圍內非3倍數的自然數,假設取值正確的n值,既能使式(2P′+6)-(3+2n)=a,又能使(3+2n)=b,兩式相加2P′+6=a+b為真。
(三)證明3:P=P′+1
1.證明公式(方程組)
∵P=P′+1,∴y=2(P′+1)+6,則有:
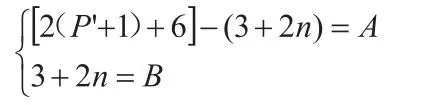
為方便下面的證明,采用簡化后方程組(下稱“原方程組”)代替上面的方程組,見第一節中(1)式和(2)式組成的方程組。
2.推導證明“猜想成立”之方法
“原方程組”中,A和B均為奇數(包含質數),可再簡化為只含質數的方程組(目的是揭示各參數之間相互關系,達到證明“猜想”之目標),即:


與證明3推導證明過程相同(省略),即方程組有解。
鏈接舉例:
∵把證明3舉例P′=3,代入證明2,則y=2P′+6=2×3+6=12。
∵y=12,∴n取值為0和1共2個自然數,代入二(二)節證明方程組中,正確值為:7+5(n=1,2n=2)。∴證明2正確。
三、結論
【重要更正】 因未細致檢查,“改進創新的坐標系證明哥德巴赫猜想之再研究”一文存在錯誤:關鍵詞“教學模型”應為“數學模型”;第二節“因系3的約數,故舍去”應為“因是3的倍數,故舍去”;末尾x取值范圍“0≤x≤y-3”應為“0≤x≤-3”,請諒解。
[注1] 什么是皮亞諾公理? 360問答2013年11月14日
[注2] 無窮大運算 360問答2013年4月6日

