不等式證明的方法研究

黑龍江省哈爾濱市工業大學附屬中學校 張天慧

不等式是高中數學教學內容中的一個重要組成部分，是研究其他數學問題的重要工具。不等式的證明方法有很多，涉及高中數學體系的方方面面。調查表明，學生在進行證明時往往無法快速地選擇出最合適、最簡便的方法，因此，教師如何將證明不等式的方法有效地滲透給學生，成為高中數學教學的一個重難點。

一、研究不等式證明的教學意義分析

首先，不等式是高中數學知識體系中一種廣泛被使用的輔助工具，在其他很多數學問題的分析與解答中都需要使用到不等式的知識，但是在使用不等式的過程中，很多時候需要我們先證明不等式的可行性。因此，研究不等式的證明方法是教學的切實需求，是學生學習數學知識的必經之途。

其次，在不等式證明教學中可以有效地鍛煉學生的邏輯思維能力。不等式證明的方法非常多，在高中數學中只涉及了一些關鍵的研究方法。在這些方法的教學中，滲透著經典數學思想的精髓，通過記憶與推理的緊密結合，可以有效地達到鍛煉學生邏輯思維的目的。

最后，通過嚴謹的不等式證明方法的學習，可以幫助學生養成嚴謹思考的習慣，培養學生良好的學習精神和習慣，這種行為習慣的形成對學生綜合素養的提升具有重要的幫助，對學生其他科目的學習也有很大的幫助。

二、兩種不等式證明的方法教學探討

在高中階段需要學習的不等式的證明方法有很多，主要用到的有放縮法、柯西不等式、比較法、反證法、換元法等。下面，我將針對放縮法和柯西不等式兩種主要的方法進行教學講解。

1．放縮法

放縮法是指要證明某個不等式如A＜B，可以首先將不等式的一邊進行放大或者縮小，尋找一個中間量，如將A放大成為C，如果我們可以首先證明C＜B，那么比C還要小的A自然也要小于B，即A＜C＜B，實際上是使用了不等式的傳遞性，而這種間接證明的方法就被稱之為放縮法。放縮法是研究不等式證明方法里常見的一種方法，它是通過思想轉換來實現證明的，對學生思維具有很重要的啟發作用，在教學過程中應當得到教師的足夠重視，幫助學生對放縮法的使用做到熟能生巧。放縮法的含義非常簡單，在教學中最重要的是培養學生的使用意識，當面對此類題型時，學生可以一眼看穿，直接使用放縮法進行迅速證明。下面我們用一個經典例題來看看放縮法的具體使用過程。

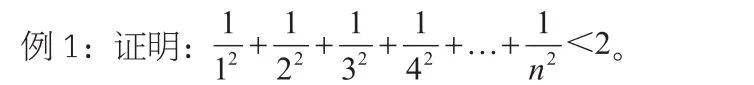
分析：這是一個基本又經典的利用放縮法來證明不等式的題目，在解答這個題目時，我們可以看到這個題目屬于A＜B的類型，于是我們可以首先將不等式左邊的A進行放大，可以首先得出：可以看出在這個不等式中的右邊是我們非常熟悉的一個式子，可以通過裂項來計算，得出不等式右邊等于2-＜2，于是證明了原不等式。

使用放縮法進行不等式的證明時，有一些有效的技巧可以讓學生記住：遇見分式可以嘗試放大或者縮小分子或者分母；構造出等比數列進行放縮；利用裂項求式來進行計算放縮；利用錯位相減來進行放縮等。教師需要在教學中積極總結題型經驗，把握命題規律，提升學生快速解決不等式證明問題的能力。

2．柯西不等式

柯西不等式同樣是不等式證明中的一個重要方法，柯西不等式具有多種形態，我們通過柯西不等式的一般形態進行講解。柯西不等式的一般形態為（a2+b2）+（c2+d2）≥（ac+bd）2，在實際使用過程中，我們經常會對這個公式進行變形，因此，一般還會用到ac+bd≤，等號成立的條件是有且僅有ad=bc，這個公式就代表柯西不等式。除了上面的一般形式，柯西不等式還存在向量形式、三角形式、概率論形式、積分形式等多種表現形式，也因此在教學中有著廣泛的應用。下面，我們通過一個簡單的例題來具體探討柯西不等式在不等式證明方面的應用途徑。

例2：已知三個正數a，b，c互不相等，證明：

分析：這個不等式剛看上去很難掌握其中的關鍵，因此我們首先可以通過變形來獲得其中的關鍵。由于三個分母都是正數，所以我們可以首先將不等式右邊的分母移到左邊來，可以獲得：對這個式子通過一系列的化簡，可以得到該式子≥=（1+1+1）2=9，又由于三個字母互不相等，所以需要注意等號是取不到的。

使用柯西不等式來證明不等式時的技巧一般是通過拆常數、湊常值來進行的。柯西不等式是不等式證明方法中一個常用但是困難的方法，需要教師為學生多總結解題經驗，找到其中的規律，最重要的是要讓學生多做題，自己找出其中的規律，對這幾種常見的題型做到爛熟于心，從而迅速地解決問題。

除了放縮法和柯西不等式法之外，在高中數學教學中涉及的不等式證明方法還有很多，需要教師為學生進行一一細致講解，可以通過一些經典例題的講解幫助學生真正地理清其中的區別與聯系，使學生在解題時能夠迅速地找出解決問題的最適合方法，并提升學生的解題能力，培養數學核心素養。