解析幾何中巧用圓錐曲線定義解題的探索

江蘇省宜興第一中學 張郡麟

定義是揭示事物本質屬性的思想形式，面對一個數學對象，回顧它的定義，常常是解決問題的銳利武器。圓錐曲線的第二定義體現了“形”的統一，第一定義則體現了“質”的區別，兩種定義不僅在解題中應用廣泛，而且具有很大的靈活性。第一種定義和第二種定義的靈活轉換常常是打開解析幾何問題思路的鑰匙，在題目中挖掘這些隱含信息有助于解題。下面我們一起來看看圓錐“定義”在求解圓錐曲線問題中有哪些常規應用。

分析：本題的解題關鍵在于巧用橢圓的第一定義，首先解出橢圓的長半軸長a，然后利用勾股定理求出半焦距c，從而構建出橢圓方程。

【例題2】（1）一動圓與圓x2+y2=1外切，而與圓x2+y2－6x+8=0內切，那么動圓的圓心軌跡是什么？（2）已知點M(－3，0)，N(3，0)，B(1，0)，⊙O與MN相切于點B，過M，N與⊙O相切的兩直線相交于點P，則P點的軌跡方程為__________。

解答：（1）已知圓x2+y2=1的圓心為O(0，0)，半徑為r1=1，

圓x2+y2－6x+8=0的圓心為A(3，0)，半徑為r2=1。

設動圓的圓心為P，半徑為r，則|PO|=1+r，|PA|=r－1，

則有|PO|－|PA|=2＜|OA|=3，所以動圓的圓心軌跡為雙曲線的一支。

（2）|PM|－ |PN|=|PA|+|AM|－ |PC|－ |CN|=|MA|－|NC|=|MB|－|NB|=4－ 2=2。

∴P點的軌跡是以M，N為焦點的雙曲線的右支，c=3，a=1，b2=8。

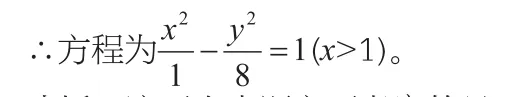
分析：這兩個小題主要考察的是雙曲線的第一定義，構造出兩個相減后等于一個常數的點點距離，然后注意到與雙曲線定義的不同點，得出所求軌跡只能是雙曲線的一支。

【例題3】設F1、F2是雙曲線x2－y2=4的左、右兩個焦點，P是雙曲線上任意一點，過F1作∠F1PF2的平分線的垂線，垂足為M，求點M的軌跡方程。

分析：一般情況下，距離之和有什么最值？距離之差有什么最值？現在要求PA+PF的最大值，那我們可以怎么轉化呢？首先利用橢圓的定義轉化為距離之差，PA+PF=PA+(2a-PF1)，其中F1為橢圓左焦點，然后將PA+(2a-PF1)寫成2a+(PA-PF1)，最后利用數形結合法“三點共線”來確定所求P點即為AF1的延長線與橢圓的交點。

我們在解有關圓錐曲線的問題時，如果題目涉及焦點、準線方程、離心率、圓錐曲線上的點這四個條件中的三個，我們一般就要聯想到圓錐曲線定義，有時甚至只要知道其中的兩個條件，也可以聯想到圓錐曲線定義。靈活巧妙地運用圓錐曲線的定義，將會帶給我們意想不到的方便和簡單。圓錐曲線的定義反映了它們的基本特征，理解定義是掌握其性質的基礎。因此，對于圓錐曲線的定義不僅要熟記，還要深入理解細節部分，比如橢圓的定義中要求|PF1|+|PF2|＞|F1F2|，雙曲線的定義中要求||PF1|-|PF2||＜|F1F2|。這樣，在解題過程中才不會步入歧途。