關于初中“最短路徑問題”的教學之悟
曹俊玲

摘要:在中學數學學習中,大部分學生一旦涉及運用性的問題時,就感到無從下手,特別是在建立數學模型和綜合運用數學知識解決問題等方面。本文以初中數學教學中“最短路徑問題”為例,提出了一些心得。
關鍵詞:初中數學? ?最短路徑問題
一、初中數學教學中“最短路徑問題”簡述
在人教版八年級上冊“最短路徑問題”的教學過程中,筆者發現,最短路徑問題的教學模型有兩個,即“牧馬人飲馬問題”和“造橋選址問題”。而運用最多的是“牧馬人飲馬問題”,它最早來源于“將軍飲馬問題”。下面,筆者重點對“牧馬人飲馬問題”進行教學分析。
二、教學效果分析
在教學過程中,“牧馬人飲馬問題”模型的教學是比較輕松的,學生也容易掌握,常考模型是兩點在直線同側。如圖1所示,其原理是兩點之間線段最短。結合軸對稱知識,將其中任意一點做出它的對稱點,再連接對稱點與另一個點,則很容易找到最短路徑。但是出題者常常結合角平分線的性質、三角形、四邊形、圓、坐標系等知識點出題,如圖2所示,由于學生在綜合運用能力上的表現不一,這就導致“最值問題”成為初中數學教學難點之一。下面,筆者以朱村中學近期期中考試的一道題目為例,進行了統計分析。
如圖3所示,△ABC為等邊三角形,D為AB的中點,高AH=10厘米,P為AH上一動點,則PD+PB的最小值為 ______厘米。
解:∵點B關于AH的對稱點為C,如圖4所示
∴連接CD,則PD+PB的最小值為CD的長度
∵△ABC為等邊三角形,D為AB的中點
∴CD⊥AB
∴CD=AH=10厘米
∴PD+PB的最小值為10厘米
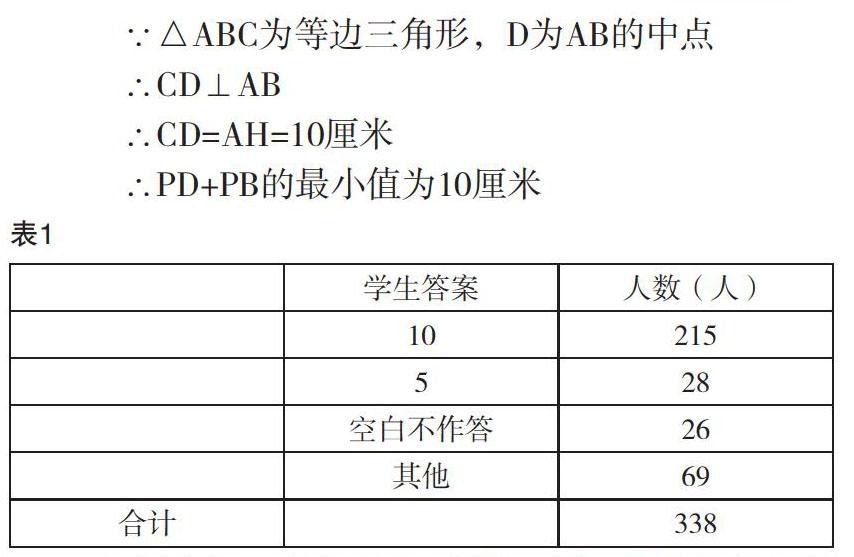
這道題為考試試卷填空題第16題,是填空題里的最后一題,其難度是比較大的,但是由于出題者將它設計為填空題,而且結合了等邊三角形的性質,學生容易根據三線合一的性質,猜到答案為10。如表1所示,學生答題的正確率為63.6%,得分率比較高。但還是有28.1%的學生不明白最短路徑原理,可見最值問題確實難度較大。
三、教學反思與感悟
1.抓住特征,理解本質
“最短路徑問題”考查的知識點主要有“兩點之間線段最短”“垂線段最短”“點關于線對稱”“線段的平移”等,其主要原型是“牧馬人飲馬問題”“造橋選址問題”,出題背景變式有角、三角形、菱形、矩形、拋物線等類型。解決此類問題的總體思路是找到點關于線的對稱點,實現“折”轉“直”。
2.歸納方法,尋找技巧
由于最短路徑問題與其他知識點具有較強的融合性,教師可以根據幾何圖形的性質靈活變式,歸納解題方法,再根據已有的模型和結論,抓住這一類問題的本質,找到解題技巧。華羅庚先生說過:“書要越讀越薄。”做題目也是這樣。題目是做不完的,但學生如果經常歸納方法,找到技巧,也可以越做越“精”,這對培養學生的數學自學能力非常有益。
參考文獻:
[1]荀峰.最短路徑問題[J].中學數學教學參考,2015,(Z2).
[2]張媛.關于初中數學最短路徑問題的探究[J].高考,2017,(6).
(作者單位:廣州市增城區朱村中學)

