田口法在永磁同步電機優化設計中的應用＊

韓愛國，苑昭*，鄭青星，徐海軍，趙尚義

（1.現代汽車零部件技術湖北省重點實驗室（武漢理工大學），湖北 武漢 430070；2.汽車零部件技術湖北省協同創新中心，湖北 武漢 430070；3.柳州五菱汽車工業有限公司，廣西 柳州 545000）

前言

近年來隨著人民對環境保護的呼聲和國家法規的要求，電動汽車已經成為汽車行業發展的新向標。驅動電機作為電動汽車的動力源，其相關研究在近十年來得到了突飛猛進的發展。內置式永磁同步電機（IPMSM）具有高功率密度、高效率、較寬的調速范圍等優良性能，已經逐漸成為當今電動汽車驅動電機的主流選擇[1]。然而永磁同步電機在運行過程中的轉矩波動現象會降低驅動效率，增大汽車行駛中的振動和噪聲，惡化行車舒適性，因此在電機設計時應使電機具有較低的轉矩波動[2-3]。另外希望驅動電機以最小的體積產生盡量大的功率和較寬的調速范圍，這就要求在電機設計時保證其具有盡量大的轉矩密度和直軸電感。

在對永磁同步電機進行優化設計時，通常選取一個或者多個結構參數進行參數化有限元仿真，這種做法簡單方便，但是仿真時間長，效率低，且具有盲目性。因此有人采用如粒子群算法和遺傳算法等優化算法進行電機優化設計[4-5]，其優點是可以自動地對全局參數變量進行尋優，可以考慮到所有的優化性能指標，但是其優化目標具體函數的建立比較復雜，計算耗時很長。

田口法是一種快速尋優的局部優化算法，自被提出以來，在電機優化設計中得到了廣泛應用[6-7]。其在電機結構優化設計上具有顯著優勢：以最少的實驗次數獲得最優的實驗參數的組合，文獻[7]通過優化設計實驗證明了田口法相比于粒子群等算法具有高效性和實用性。

內置式永磁同步電機轉子磁極結構中，嵌放永磁體的槽的尺寸位置以及永磁體的尺寸是影響電機性能的重要參數[11]，文中以永磁體槽的尺寸位置的相關參數和永磁體的寬度為設計變量，以降低電機額定電流下的轉矩波動和齒槽轉矩為優化目標，單位磁鋼寬度產生的扭矩和直軸電感不小于原機性能為約束條件，在ANSYSMaxwell有限元仿真軟件中采用田口法進行優化設計，將優化后的電機性能與定子斜槽方案進行對比，并對比優化前后峰值電流下的性能變化，以綜合考察電動汽車在勻速行駛和急加速行駛時驅動電機的動態性能。

1 IPMSM電機模型和主要參數

本文以48槽8極內置式“V”型轉子磁極結構的永磁同步電機作為優化對象，一極下的定轉子結構及部分參數如圖1所示，原機的基本參數如表1所示。

在“V”型轉子磁極結構中，空氣槽的形狀和永磁體的尺寸是影響電機性能的重要因素，如圖1標注所示，其參數分別是磁橋寬度a、空氣槽厚度b、同極永磁體間加強肋寬度k、空氣槽中部距轉軸徑向長度h、永磁體極間長度r、r的高度d、單塊磁鋼寬度w，磁鋼厚度t。

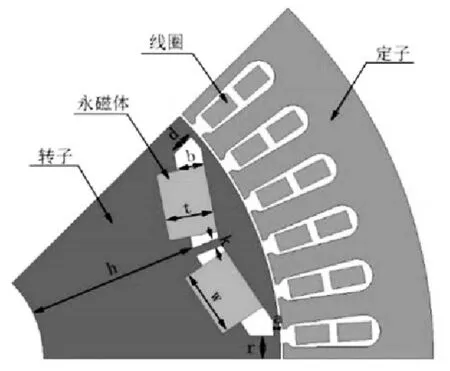
圖1 定轉子結構及部分參數示意圖

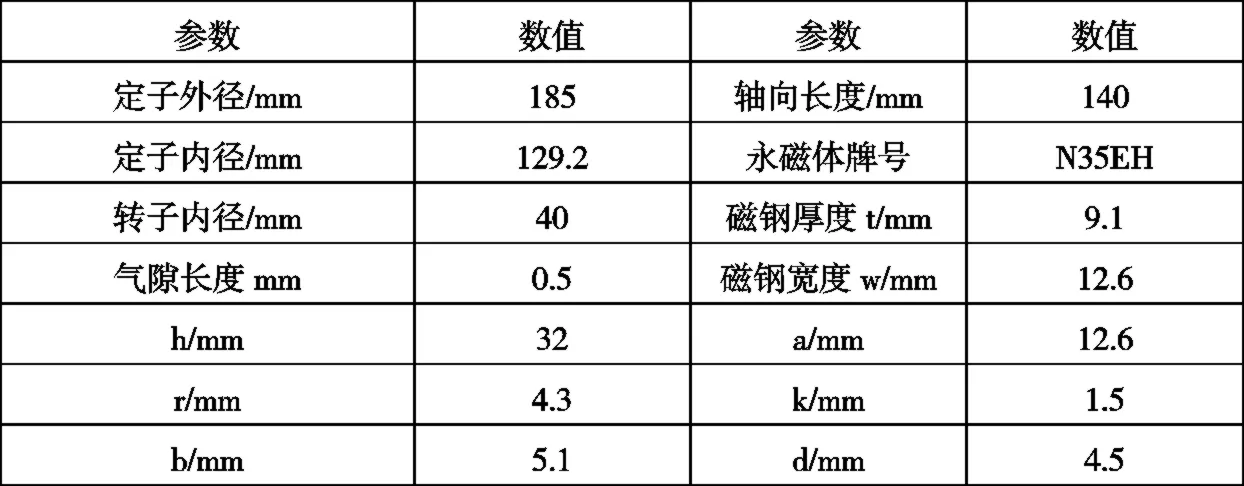
表1 IPMSM基本參數

2 基于田口法的電機性能優化

田口法是日本質量控制專家田口玄一融合正交實驗的優點和信噪比技術的特點而創立的一套優化方法，其特點是通過正交表安排各參數的各水平組合，是一種對優化參數變量進行正交表實驗設計的局部優化方法，其顯著優點是可以通過最少的實驗次數來獲得優化參數的最佳組合。因此可以在電機有限元仿真軟件中應用田口法來快速獲得理想的仿真結果。

田口法實驗設計的主要分為三個步驟：

（1）確定優化因子及其水平，建立優化目標；

（2）建立正交表，對各次實驗進行有限元仿真；

（3）對各實驗的計算結果進行平均值和方差分析，得到各因子對優化目標的影響比重，選取并驗證最優的各因子水平組合。

由于磁鋼厚度 t會影響電機的抗退磁能力，磁橋寬度 a與轉子結構強度有關，因此為保證電機的抗退磁能力和轉子結構強度，將圖1中除a和t外的其他參數取為優化因子，各因子取5個水平，表2給出了各因子水平取值，這些因子的取值考慮到了空間限制、設計精度和實際生產工藝的允許精度。

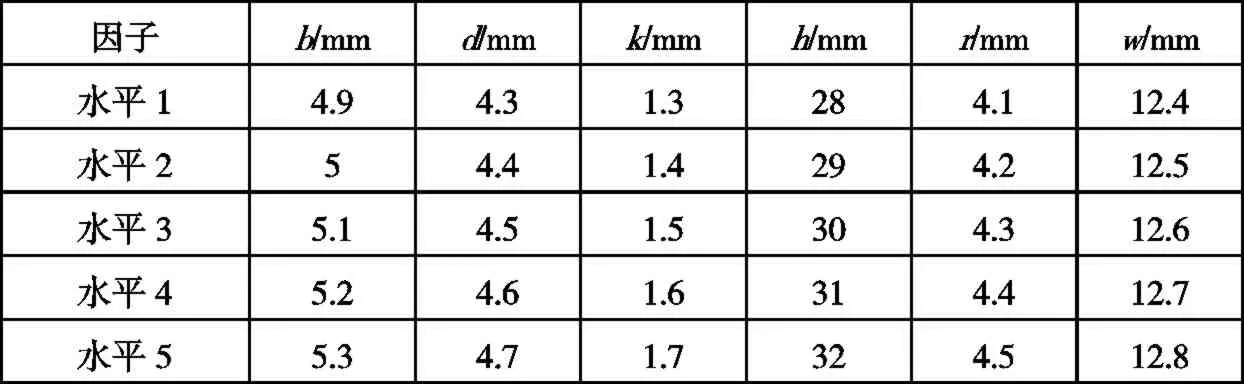
表2 各優化因子及其水平取值

選取的優化目標有：單位磁鋼寬度產生的平均轉矩Ta、直軸電感Ld、轉矩波動率Kt和齒槽轉矩峰值Tc。其中，單位磁鋼寬度產生的平均轉矩Ta的表達式如式（1），轉矩波動率Kt的表達式如式（2）。

式中Tavg是穩態下瞬時轉矩的平均值，w是單塊磁鋼寬度，Tpk2pk為穩態下瞬時轉矩的極差。

2.1 正交矩陣及仿真分析結果

本文設計的實驗因子個數為6，水平數為5，若按照傳統的全因子全水平設計，即每一種組合都需要做一次有限元仿真計算，此時總共需要做56=15625次計算。而利用田口設計方法建立正交實驗矩陣時只需要52=25次計算，極大縮短了實驗計算時長。這種正交矩陣可使各因子的不同水平在每列中出現的次數相等，任意兩列間橫向組合的搭配是均衡的。通過對正交表的計算結果進行平均值和方差分析可以得到每個因子水平的擬合優化目標值，可以得到類似于傳統全因子全水平的效果。實驗矩陣中各因子下的數字分別對應表2中的各水平值。這里以額定電流下的性能指標進行優化設計，該工況點下的實驗矩陣表及其對應的優化目標值如表 3所示。

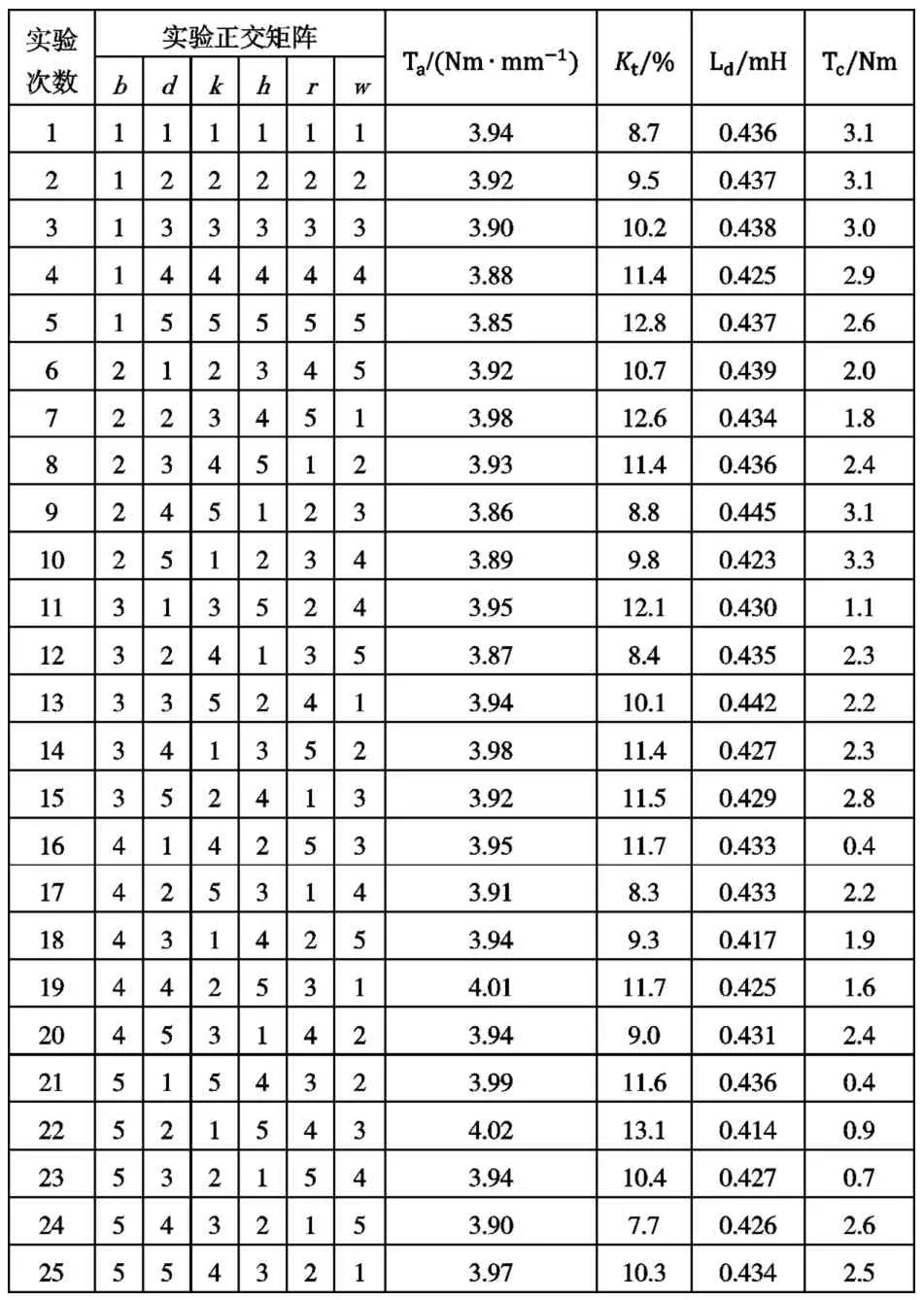
表3 實驗正交表及各優化目標值

2.2 實驗結果分析

根據田口法理論，不僅可以根據表3中的數據得到各優化目標的全體實驗平均值，還可以得到各參數水平下的優化目標值。從而可直觀的得到各優化目標的最佳參數水平組合。

各優化目標的全體平均值結果見表4，其計算公式如(3)所示。

式中，m為表 3中某一優化目標的全體實驗平均值；n為全體實驗次數；mi為第i次實驗下某一優化目標值。

表4 各優化目標全體實驗平均值

接下來計算各優化目標在各因子水平下的平均值，例如計算直軸電感Ld在因子b水平1下的優化目標值，其計算公式如式(4)所示，同理可計算其他各因子水平下的優化目標值。計算結果見表5。

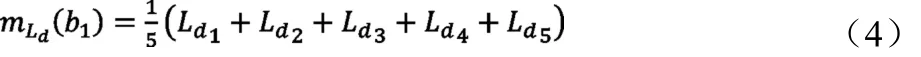
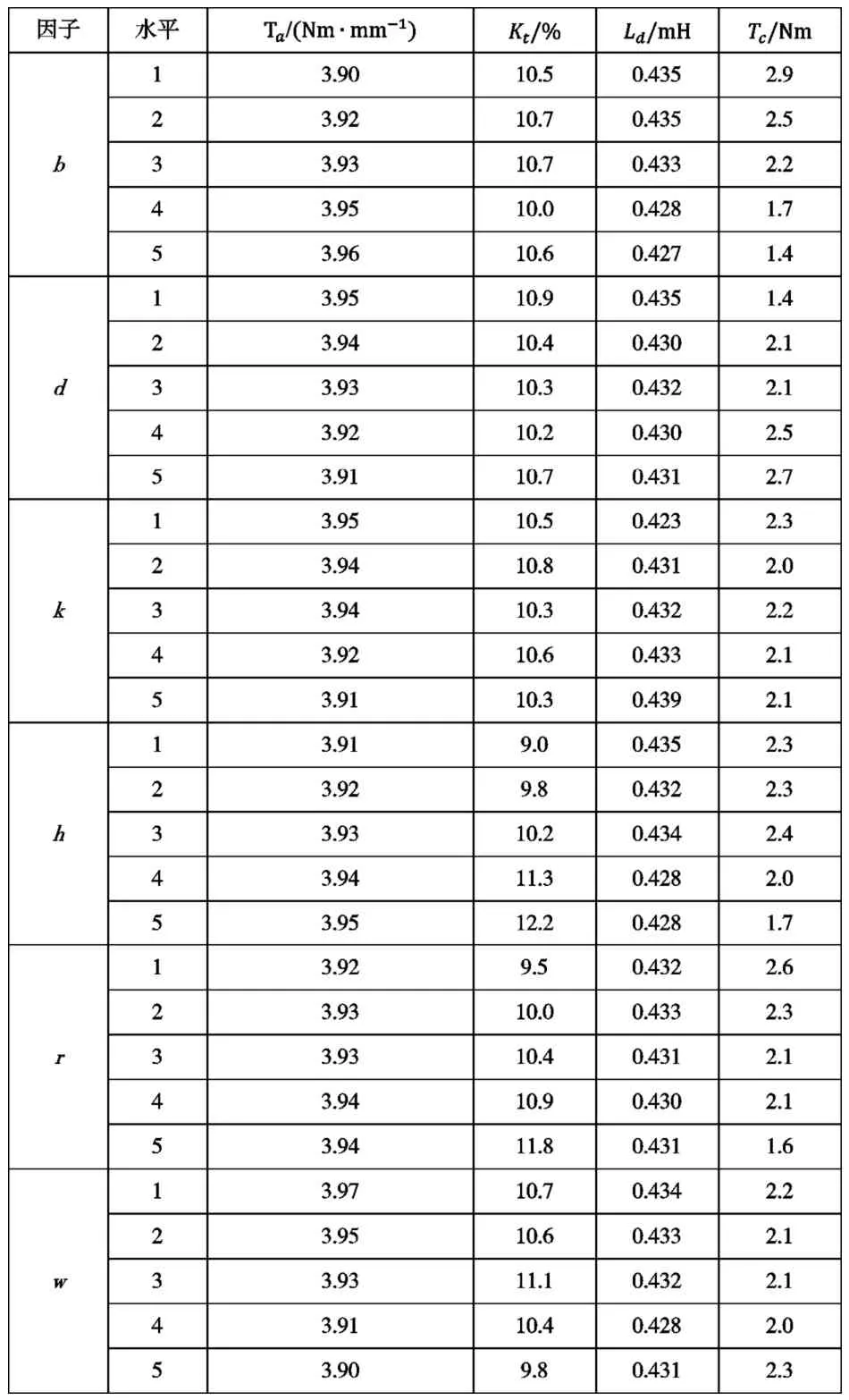
表5 各因子水平下的優化目標值

式中，Ld1～Ld5分別是表3中在因子b水平1下的進行的1～5次實驗的直軸電感值。

從表5可以看出，單位磁鋼寬度產生的平均轉矩Ta隨著b、h和r的增大而增大，隨著d、k和w的增大而減小；轉矩波動率Kt隨著h和r的增大而明顯增大；直軸電感Ld隨著k的增大而明顯增大；齒槽轉矩峰值Tc隨著b和r的增大而明顯降低，隨著d的增大而增大。因此可得到使單位磁鋼寬度產生的平均轉矩 Ta最大、轉矩波動率 Kt最小、直軸電感Ld最大、齒槽轉矩峰值 Tc最小的參數水平組合分別為b(5)d(1)k(1)h(5)r(5)w(1)、b(4)d(4)k(3)h(1)r(1)w(5)、b(2)d(1)k(5)h(1)r(2)w(1)、b(5)d(1)k(2)h(5)r(5)w(4)。顯然使所有的優化目標結果最優的各因子水平組合不同，此時需要通過方差分析得到各參數對優化目標的影響程度，從而得到最佳的參數水平組合。

通過方差分析可評估因子變化對各優化目標的影響程度。方差計算公式如(5)所示。

式中，SA為在因子A下某一優化目標的方差；Q為各因子的水平數，即Q=5；mA(j)為表5中因子A在水平j下某一優化目標的值；m為某一優化目標的全體實驗平均值。

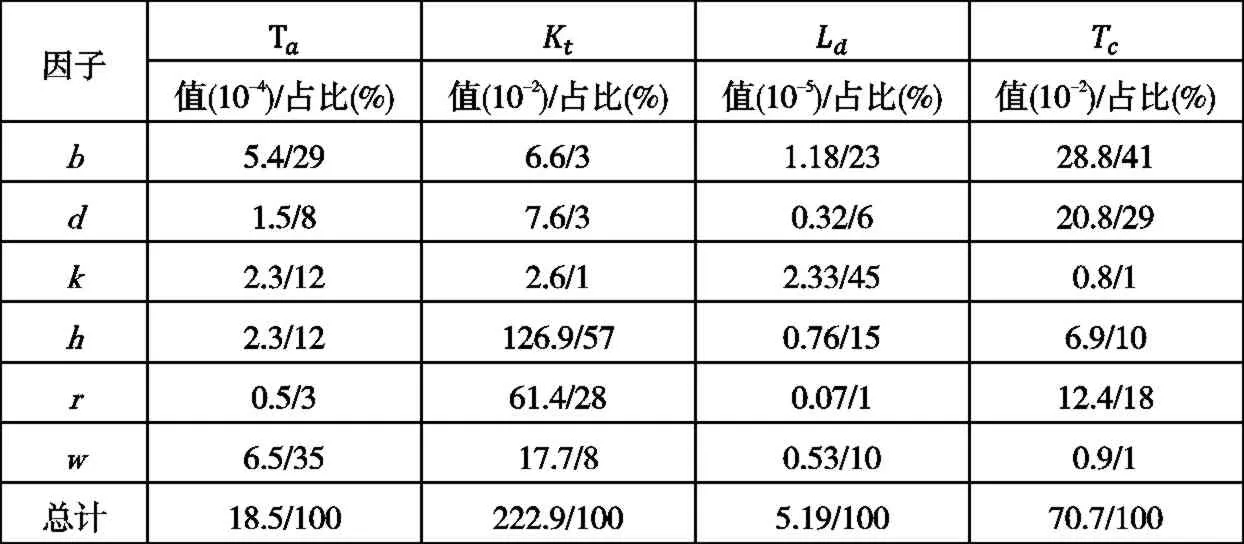
表6 各因子對優化目標的方差及影響程度

從表6可以看到各因子對各優化目標的影響程度。結合表 5和圖 2可以看出，對單位磁鋼寬度產生的平均轉矩 Ta影響最大的因子是w，其次是b；對轉矩波動率Kt影響最大的因子是h，其次是r；對直軸電感La影響最大的因子是k，其次是b；對齒槽轉矩峰值Tc影響最大的因子是b，其次是d。

2.3 確定優化后的因子水平組合

根據以上分析，以降低轉動波動率 Kt和齒槽轉矩峰值Tc為優化目標，保持單位磁鋼寬度產生的平均轉矩Ta和電機的直軸電感Ld不小于原機性能為約束條件時，參數b、d、h和r的選取以轉矩波動率Kt和齒槽轉矩峰值Tc最小為準，參數k和w的選取以單位磁鋼寬度產生的平均轉矩Ta和直軸電感 Ld最大為準。最終確定的各因子水平的最優組合為b(5)d(1)k(5)h(1)r(1)w(1)，其組合的各水平值如表7所示。

表7 優化后各因子取值

2.4 優化結果分析

將田口法優化后的因子水平組合在有限元軟件中進行仿真，得到的結果見表8所示。相比于優化前原機性能，優化后電機額定電流下的轉矩波動率 Kt和齒槽轉矩峰值 Tc分別減少37.2%和5.6%，這兩項性能值越小越好，此時驅動電機轉矩波動小，有利于降低驅動電機的振動噪聲；直軸電感Ld增大了 3%，此時驅動電機具有更大的調速范圍，但是單位磁鋼寬度產生的平均轉矩Ta沒有變化。

表8 優化前后額定電流下的性能對比

優化后的在一定峰值電流下的電機相關性能如表 9所示。可以看出，此時平均轉矩 Ta和轉矩波動率 Kt分別減少1.9%和66.7%，直軸電感Ld增大2.6%。此時平均轉矩Ta略有減少，但是轉矩波動率Kt得到了大幅降低，有利于降低電機的振動噪聲，同時直軸電感Ld略有增大，利于擴大調速范圍。

表9 優化前后峰值電流下的性能對比

3 結論

在車用驅動的場合下通常關注永磁同步電機的轉矩波動率和齒槽轉矩，以降低電機的振動噪聲。本文在對車用永磁同步驅動電機進行有限元仿真時，將田口法應用于其優化設計中，得出如下結論：

以降低齒槽轉矩 Tc和轉動波動率 Kt為優化目標，直軸電感 La和單位磁鋼寬度產生的平均轉矩 Ta不小于原機性能為約束條件，得到了“V”型轉子磁極結構的空氣槽的最佳位置，實現了優化目標的大幅優化。同時優化設計后峰值電流時的性能亦得到了提升。

仿真結果表明了田口法在電機電磁仿真優化設計時的實用性和高效性，對工程實踐應用具有現實指導意義。