窮源競流話最值，數形結合助析題
——一道世界數學團體錦標賽試題引發的思考

☉浙江省臺州市三門初級中學 李如軍

一、源起

沙孟海先生在自傳中提及自己一生的書法學習過程，他用四個字“窮源競流”概括.今天我借沙先生的四個字與讀者共話解題之道.筆者在翻閱某校九年級月考卷時，發現一道填空題得分率很高，過了幾個星期之后筆者將此題作為簡答題布置給學生再做，由統計結果得知得分率很低，我很詫異.在這高低變化過程中我和學生進行了簡短的對話.

筆者：當初你是如何解決這道填空題的？

生：個人感覺應該是點E運動到中點的時候，此時F點是CD的中點.

筆者：為什么當E、F為各邊的中點時，EF最小？當E為BC的中點時，F是否也為CD的中點？

這些問題一下子把該生難住了.

一道難度系數接近0.95的填空題，很容易被教師忽視.不再深入挖掘答對的習題是當下教學中普遍存在的問題.為了給學生更充足的時間，我將此簡答題作為周末家庭作業，以期待更多更好的解答.

經歷過這事以后，我開始反思自己的教學與解題.有很多得分率不低的題，作為教師的我們都想當然覺得學生已經掌握了，并且能上升到推理分析的角度完整解答，其實他們只是停留在主觀臆測的層次.學生是否窮其源，謀其法，需要我們教師用“窮源競流”加以引導，下面以一道幾何題為例.

二、問題的提出

有這樣一道考題：

試題（2017新昌期末卷）如圖1，正方形ABCD的邊長為2，點E、F分別在BC和CD上，∠EAF=45°，則EF的最小值是_______.

圖1

三、競流——解法欣賞

一部分學生看到這道題后采用直觀想象的方法：在∠EAF不變的情況下，根據主觀判斷，E點從點B往點C運動的過程中，EF經歷由大到小，再由小到大的過程，那么E、F關于直線AC對稱時EF最短.即E、F分別為BC、CD的中點時，EF最小.其中有小部分學生脫離宏觀分析，直接猜測E、F為BC的中點時，EF最小.（此法記為直觀想象法，記為解法1）

在學習“旋轉”一章后，有學生結合旋轉的基本要素觀察圖形.這是一個正方形背景下的問題，想到將△ABE繞點A旋轉至△ADE′，如圖2.將一些變化分散的量集中到Rt△ECF中，利用勾股定理得到這是絕大部分學生反饋的周末作業，對于如何處理這個方程，很多學生束手無策.

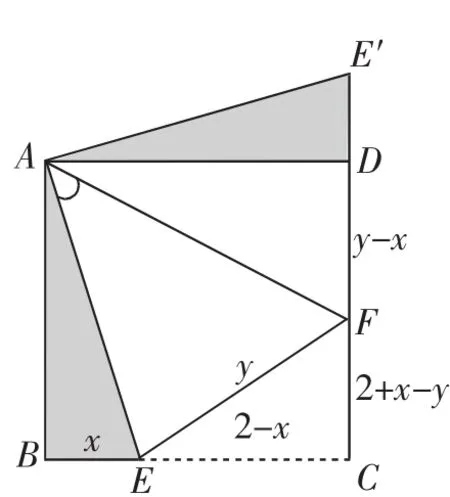
圖2

為什么用Δ法可以求得y的最值呢？有很多學生提出質疑.經過一些時間的討論后，有學生給出了解釋，如圖3、圖4.

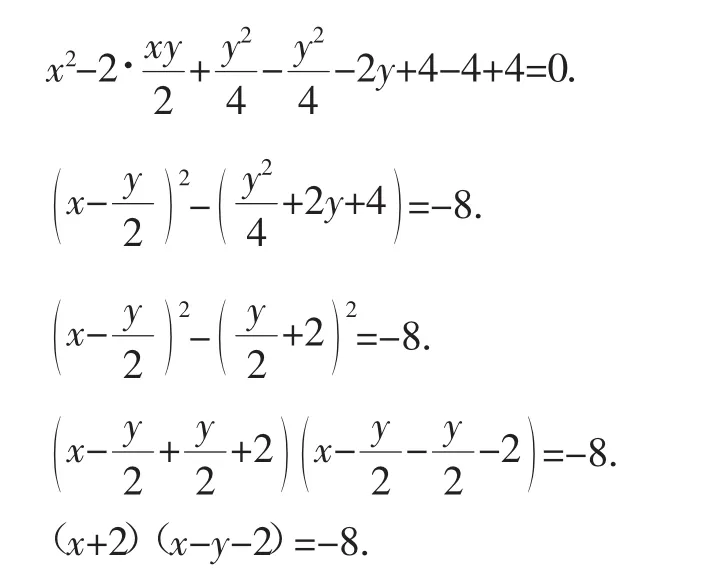
此時拋物線y1=（x+2）［x-（t+2）］必與y2=-8相交.

該生利用函數圖像解釋了參數y的最值問題，很直觀，易于接受.此類方法是從方程的角度引入未知量x，借勾股定理建立方程，再結合二次函數與一元二次方程所學內容，把用函數圖像解決方程問題演繹得淋漓盡致，同時把Δ法解釋得很完美，我們著實為善于思考的學生拍手叫絕.（不妨記該法為解法2）

圖5

圖6

筆者歸納：大家從最初的主觀想象（猜測）到方程建模，函數圖像的巧妙解析，從直觀走向理性，從微觀走向宏觀.那么，能否從函數角度直接加以解決呢？經過筆者提示后，學生自然引入變量x與y，得函數關系式可惜此函數是初中階段沒有研究過的一類新函數，無論從表達式還是函數圖像都很難得到它的函數值分布情況.故從函數角度研究其最小值是難以實現的.但是學過幾何畫板的學生還是繪制了草圖（如圖5）.從圖像中不難看出，當x近似取0.84時，y最小，約為1.61（如圖6）.盡管利用畫板可以得到圖像，但是難以精確，更何況平時沒有條件使用.

至此，山重水復疑無路.筆者回顧解法2圖形變換過程中有一個不變的量S△AEF=S△ABE+S△ADF，即 S△AEF=S△AE′F能否借助面積不變量分析法與算兩次來實現呢？如圖7，過點A作AB′⊥EF于點B′，交EF的平行線CG于點G，過C點作CC′⊥EF于點C′，設CC′=x，則AG=2+x，連接AC.由此可知

圖7

要使得EF最小，只要x最大.結合圖形可知，AG≤AC，即

除了面積的倍數關系，很巧合的是題干中給我們的兩個已知角也成倍數關系.從角度的倍數關系中是否可以再做做文章？在完成九上“圓”一章中“圓心角與圓周角”后，有學生提出這樣的做法：因為∠EAF=45°不變，聯想到圓中的圓周角，如圖8，作△AEF的外接圓圓O，連接AO、EO、FO，作EF的中點M，連接OM、CM.易得OM⊥EF，CM=EM=MF.因為∠EAF=45°，所以∠EOF=90°.設圓的半徑為r，所以所以由圖可知，A、O、M、C四點共線，即時，r最小，此時則EF=也最小.（此法記為解法4）

圖8

精彩的討論交流完畢，有一位學生聯想到曾經遇到的一道世界團體錦標賽試題.

（世界團體錦標賽試題）如圖1，點E和F分別是正方形ABCD中，BC邊和CD邊上的點，且∠EAF=45°，求的最小值.

往常覺得很難的問題，如今變得簡單了.此題解法此處不再贅述.至于新昌期末卷、團體錦標賽試題孰源孰流無從考證，抑或是一種巧合，經歷這場討論后，學生收獲了這樣的感受：難題無非是簡單問題的疊加，只要窮源競流多歸納，再難的問題也可以輕松解決.

四、解后反思

1.構造模型巧轉化

解法3借助旋轉知識，構造一對全等三角形，得到面積相等.把EF最小問題轉化為線段AG最大問題，在解題過程中深切感受到面積法數形兼備，能把代數、方程中不變量分析法、算兩次等思想方法融為一體.這種技法其實源于教材.“表示相等關系的式子叫等式”，這是教材中普通的話語，表現在數量上，我們通常要從不同的角度算兩次，才能得到好的結果，人教版八下“勾股定理”的證明就是這種思想的美妙呈現.解法4是構造一個外接圓，把EF最小問題轉化為折線段最短問題，即兩點之間線段最短問題.此題的隱圓使用得非常漂亮.可以釋放∠EAF=45°這個特殊的條件，只要0°＜∠EAF＜90°都可以通過此法解決.

當然，我們也可以通過構造方程模型、函數模型加以解決，只是主元法與新函數的研究貌似有點兒超綱，但是還是源于教材的.

2.數形結合妙解析

幾何問題代數化就是數形結合最好的體現，無論是方程還是函數，都是代數化的表現形式，而參數方程最值問題（Δ法）處理過程中又離不開函數及其圖像的支撐，華羅庚先生說得好“數缺形時少直觀，形缺數時難入微”.解法1中暴露了“難入微”的尷尬.

3.宏觀把控憶舊知

波利亞在《怎樣解題》中指出：當問題比較困難時，我們可能很有必要進一步把問題再分解成幾部分，并研究其更細微的末節.所以研究幾何圖形，一個基本方法就是教學中引導學生建立一個完整的知識網絡，讓學生的思維游走在一張四通八達的網上，教學中引導學生窮源競流，相互交流碰撞出思維的火花，歸納出方法網，只有這樣，解題的思維才能找到著力點，思維開闊，游刃有余.解得一法后歸納其法才能演繹出更多更好的問題解決之法.