靈活應用換元法解決數學問題
☉山東省濟南市萊蕪區雪野鎮中心中學 畢平思
學習了二元一次方程組的解法后,我們知道解二元一次方程組有兩種基本方法:代入法和加減法.下面讓我們看看如何解方程組根據方程組的特點,常規解法是采用加減法.比較兩個未知數的系數,我們發現消去x比較簡單,解法如下.①×7,得14x+21y=84③,②×2,得14x-34y=194 ④.③-④,得55y=-110.則y=-2.把y=-2代入①,得2x+3×(-2)=12.則x=9.則原方程組的解為上述解法其實是一種常規解法.本題其實可以應用均值換元法巧解.若實數m、n滿足m+n=p,則可設我們稱這種換元方法為均值換元法.觀察方程①,根據系數特點,可設2x=6+6t,3y=6-6t,即x=3+3t,y=2-2t.代入方程②,得7(3+3t)-17(2-2t)=97.則t=2.則x=3+3×2=9,y=2-2×2=-2.不難發現,采用均值換元法解原方程組,大大減少了運算量,提高了解題效率.實際上,換元法也是一種重要的數學解題方法.在解決數學問題時,有時可以把某個式子看成一個整體,用一個變量去代替它,從而使問題得到簡化,叫作換元法.換元法的種類比較多,均值換元法只是其中的一種.應用換元法可以起到化難為易、化繁為簡之效,從而提高解題效率.
一、用于計算
分析:由于括號內加數太多,此題若直接計算,無論是先對括號內通分,還是應用乘法分配律,都不現實.注意到括號內有許多相同的項,如可以先將這些相同的項看成一個整體并用字母表示,再計算就方便多了.
解:令則原式
評注:本解法實際上是雙參數換元,即在換元時引入兩個字母(或參數).通過換元可以發現,換元之后原式變得非常簡捷,而且在計算時相同項可以相互“抵消”.
快樂體驗:已知且都是正數,試比較M、N的大小,并說明理由.
二、用于解方程組
分析:本題若按常規解法,需要先對方程組進行化簡,比較麻煩,且易出錯.若能注意觀察到兩個方程中都含有可分別視為一個整體,然后運用整體換元的方法求解.
快樂體驗:解方程組
例3已知關于x、y的二元一次方程組的解是則關于x、y的二元一次方程組的解是______.
評注:本題若按常規方法,需要將代入方程組①求出再把代入方程組②,得到另一個方程組再解這個方程組,得這樣解步驟甚多、運算繁雜,容易產生錯誤.仔細觀察方程組①和②,對比兩個方程組的結構.若設x+y=u,x-y=v,則方程組②可變形為方程組③對比方程組①和③,我們發現這兩個方程組除了未知數的表達形式不一樣,未知數的系數和常數項部分都相同,因此它們的解相同,則即解這個方程組,得顯然這樣求解非常簡捷.
快樂體驗:已知方程組的解是則方程組的解是( ).
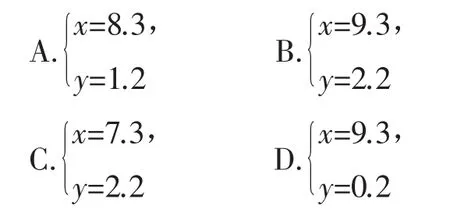
三、用于求二元二次方程的實數解
例4方程x2-xy+y2-x-y+1=0的實數解是_____.
評注:本題若按常規方法,可以先將原方程整理成關于x的一元二次方程,得x2-(y+1)x+(y2-y+1)=0.由方程有實數根的條件,得一元二次方程的判別式即(y-1)2≤0.而(y-1)2≥0,于是(y-1)2=0,則y=1.
將y=1代入原方程,得(x-1)2=0,則x=1.
則原方程的實數解為x=1,y=1.
其實本題若用二元代換求解,非常簡捷.由于對于任意實數,恒有令則x=a+b,y=a-b,這種代換就叫作二元代換.二元代換是一種非常重要的換元方法,利用二元代換解決數學問題同樣可以起到化繁為簡、化難為易之功效.下面利用二元代換解答本題:
則a=1,b=0.則x=1,y=1.
則原方程的實數解為x=1,y=1.
快樂體驗:方程x2+xy+y2+x-y+1=0的實數解是_____.
以上僅通過三例說明了換元法在解決數學問題時的作用.換元法的應用還有很多,如我們可以利用換元法解分式方程,如解方程利用換元法解無理方程,如解方程利用換元法解分式方程組,如方程組的解是______(可先對方程組中的每個方程兩邊分別取倒數,將原方程組變形為的形式,然后再采用換元法);利用換元法化簡分式,如已知:x+y+z=3a(a≠0,且x、y、z不全相等),求的值.希望大家在今后的學習中認真總結,看看哪些數學問題適合應用換元法,并盡可能掌握這種方法,從而提高解決數學問題的效率.W

