開展數學寫作研究，促進錯題深度訂正*

☉江蘇省南京市蓮花實驗學校 吉明華

利用數學寫作促進學生數學學習的研究得到很多一線教師的喜歡，不少數學期刊也經常有類似的研究心得的文獻，研究者們關注的往往是數學寫作的類型（如數學小論文、數學日記、數學周記、數學作文、數學反思小文章等），而對數學寫作的功能特點的探討泛泛而談偏多，缺少更為細化、更有針對性的功能特點的研究.本文先分享近期收集到的七年級學生數學寫作案例，并主題關注數學寫作如何促進錯題深度訂正.

一、學生圍繞聽課筆記梳理而成的數學寫作案例與評析

案例1：《知其然，知其所以然》，七年級學生Z.

今天上課老師主要講評了單元測驗試卷，題目多數是老師以前就講過的，沒考好的原因主要集中在粗心上.

雖然下面這道題練過、講過多次，我還是錯了.反復思考，我覺得這道考題很有意思.

已知，a、b在數軸上的位置如圖1所示，化簡|a|-|a-b|＋2|a＋b|.

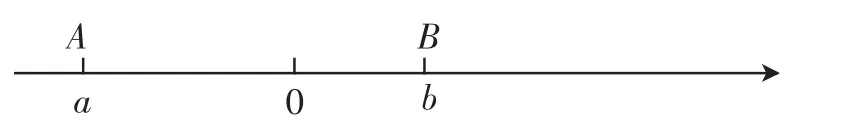
圖1

看著這一個個絕對值符號，我仿佛看到了不可跨越的長城.不過試卷上的長城，只要掌握技巧，便可輕松躍過，經常在這種題目上跌倒的我立刻敲響警鐘，努力回憶老師講的解法步驟.

第一，“明敵軍主力”，判斷絕對值符號內結果的正負.

由圖可知，a＜0，b＞0，|a|＞|b|，所以a＜0，a-b＜0，a＋b＜0.

第二，“哭長城”，去絕對值號.我們要拿出孟姜女的精神，讓長城不再那么堅固，同時我們要使用“留白藝術”，每個絕對值內都是負數，那么先把絕對值改為小括號，再在前面添加負號，此時絕對值外所有部分都還未添加，“留白”是為了給它們空出位置，現在要將它們補上去了，再適當添加中括號.

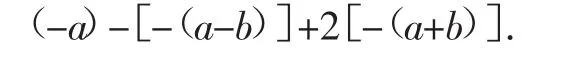
第三，“清理廢墟”，最后就剩下化簡了，運用去括號的規律，再合并同類項，便可得到答案

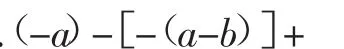
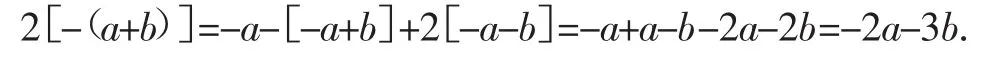
“長城之戰”，考生獲得勝利！

老師評析：Z同學這篇生動形象的“攻破長城”主要關注的是絕對值符號化簡問題，這是一類高頻問題、必考題型，不但有效考查絕對值的概念，又對添括號、去括號、合并同類項等技能有“綜合”要求.可以說，一份七上期中試卷往往因為這種題型的出現，就能“阻擋”相當一部分學生向高目標分挑戰.

Z同學用“三部曲”化解難點，形象生動，這就是“明敵軍主力”：判斷絕對值符號內字母或式的正負；“哭倒長城”：化去絕對值；“清理廢墟”：化簡結果.

只要能嚴格執行她提出的這個“三部曲”，這類問題一般都能順利求解.我們看到的很多錯例中，在“三部曲”的每一步都有學生出錯，從而導致解題失敗，是值得學習者認真體會的.

特別欣賞的是，關于去絕對值符號這一步驟的講解，小作者使用了不同顏色進行書寫表達，并提醒“留白”漸次生成，這些不正是很多數學教育家們所倡導的“數學活動經驗”嗎？

從數學求真的角度看絕對值符號如何向小括號轉化這一步驟，需要“回到概念”，認真想清絕對值的定義、幾何意義，就知道化去絕對值符號后要成為“非負數”，這需要對絕對值符號內的數、字母或式子的正負有精準辨析，據此就溝通了第一步與第二步，“三部曲”也就渾然一體，不可分割.理解這點，就從簡單的“三部曲”能做對習題“知其然”層次，走上了深刻理解的“知其所以然”的境界了！

案例2：《學好數學要有“序”》，七年級學生T.

數學是一門奇妙的學科，說它容易卻有點兒難，說它難卻又很簡單、好懂.它有各式各樣的表達形式，只要我們學懂了概念，掌握了方法，就會覺得很輕松，很多問題其實是換湯不換藥.學好數學不能只掌握方法，還要有敏銳的洞察力、縝密的思維和細心的計算，例如，最近學習的整式的加減，我還是有一些化簡方面的錯誤，究其原因，主要是讀題太快，跳步太多，所以我要在這篇數學寫作中對一些化簡上的錯誤做一些反思.比如，認真讀題后，不能無目的化簡，要做到“有序”思考，當然還可以做上不同的記號，以便幫助我們正確進行整式的化簡運算.

比如：a＋b＋c-b＋c.

如果直接合并，容易看漏、看錯，可以先做上標記，如下：

=a＋（b-b）＋（c＋c）

=a＋2c.

有些時候，除了計算的“序”，還要注意數字或字母書寫上的規范，比如，有人容易把數字5寫成3，或者x與z的書寫字體不當，還有些同學把字母b寫成數字6之類的.

當然，還有一些策略，如數字與符號之間適當空一點距離，不要寫得過分“密集”或者“密不透氣”.

1905年Schulthess依據脊柱X線冠狀面上側彎的部位及數目首先將特發性脊柱側凸分為5型：頸部和胸部彎、胸部彎、胸部和腰部彎、腰部彎和雙主彎[5]，隨后Lonstein等[6]和Winter等[7]將其分為7型：單胸彎、單胸腰彎、單腰彎、雙胸彎、胸彎和腰彎、胸彎和胸腰彎、3個或以上的多彎，以上的分型是根據側凸的在X線上直觀的形態，并未與臨床治療及手術融合進行結合。

老師評析：T同學在《學好數學要有“序”》中，結合簡單的合并同類項講解了計算有“序”的步驟分解，值得一些喜好“跳步驟”的學生傾聽.此外，他還小結了很多非智力因素中的運算錯漏，如數字5的書寫不規范；對字母b與數字6辨識不清；字母x與z的書寫字體不當出錯；對a＋b-c書寫字符間距的提醒，等等.以上都是課堂板演或老師講解時提到的一些究錯細節，足以說明T同學課堂捕捉力之細致，非常難得！

案例3：《解題過程的嚴謹與全面》，學生L.

一眨眼，單元測試又到了，對于這次考試的錯題，我也有分析，做錯的題目為“對于任意有理數x，比較多項式4x2-5x＋2與3x2-5x-2的值的大小”.

讀完題目，我便知道，如果運用“作差法”便會輕易地求出結果.于是，便有了如下的過程：

解：（4x2-5x＋2）-（3x2-5x-2）

=4x2-5x＋2-3x2＋5x＋2

=x2＋4.

因為x2＋4＞0，所以4x2-5x＋2＞3x2-5x-2.

自認為萬無一失的我卻在批改后的試卷上看到了扣掉的分數.于是滿心疑惑，便認真地對照了老師的解答過程：

解：設4x2-5x＋2=A，3x2-5x-2=B.

A-B=（4x2-5x＋2）-（3x2-5x-2）

=4x2-5x＋2-3x2＋5x＋2

=x2＋4.

因為x2≥0，所以x2＋4＞0，所以4x2-5x＋2＞3x2-5x-2.

所以A＞B.

相比較后，我發現與老師的不同點只有2處，一是開頭的“設4x2-5x＋2=A，3x2-5x-2=B”，二是末尾“因為x2≥0，所以x2＋4＞0”，短短兩行，到底有多大的奧秘呢？

我思考起來.開頭的“設4x2-5x＋2=A，3x2-5x-2=B”,不僅可以使下面的“作差法”來得簡潔、工整，還可以直接明了地讓人理解過程的用意.而末尾的“因為x2≥0，所以x2＋4＞0”更能解釋為什么“x2＋4＞0”.這樣的過程相對來說更全面，更嚴謹，也更值得我們學習.

因此，下一次我在做題時，不僅要講究思路和方法，還要寫好解題過程，盡可能做好我的“嚴謹與全面”.

老師評析：L同學的數學成績在班級中名列前茅，所以在批閱作業時對她的過程表達提出了很高的要求.從她這篇數學寫作來看，她對比老師的過程表示，“看”出了不同，“看”出了優化的必要，非常有意義.事實上，對于平時的測評、反饋、閱卷來說，扣分并不是目的，而是通過評價促進學生修補錯漏、改進方法.教學經驗告訴我們，有相當一部分學生并不能如L同學那樣仔細對比自己的解法與老師解法的不同，特別是辨別一些細微、細節上的表達差異，他們往往認為“差不多”，結果好像都一樣，過程少一兩步就不寫了.這種“差不多”的認識是要不得的，也是這類學生與優秀學生不斷拉開距離的一些重要原因.

二、讓數學寫作促進學生對錯題的深度訂正

根據教學經驗，整理錯題是學好數學的關鍵，但是如何整理錯題是一個大的難題，怎樣整理錯題才是有效的呢？我們的實踐表明：數學寫作是促進學生深度訂正、整理錯題的一個有效途徑.

1.用數學寫作開展錯題訂正促進學生深度究錯

究錯，不僅僅是糾錯，更要探究錯誤，從過程到結果，每一步都像是在下棋，一步出錯，滿盤皆輸.所以找到錯誤的原因才能實現“病從根本治”.通過數學寫作方式，引導學生找出錯誤，并跟進思考當時為什么錯，是哪一步想錯了，是概念不清楚，還是計算跳步驟，是否還有不同的解法……把這些逐項分析，就會得到更深刻的理解.有時還可以讓學生通過數學寫作記錄對比老師的解題過程，把初始錯誤或不夠優化的解題步驟也寫在旁邊，通過對比發現自己解題的欠缺，學會提煉其中精華，防止下次遇到類似問題時再出差錯.

2.批閱數學寫作可反饋學生對錯題的理解深度.

教師批閱學生數學寫作時，可以反饋學生對錯題的理解深度，也常常能看出學生分析錯題進程中“火熱的思考”，有利于進一步精準診評學生對錯題是否真正弄懂、達到深刻理解的程度.華東師大終身教授鐘啟泉先生倡導“對話教學”，不僅是課堂上的對話（“課上對話”）與互動，筆者認為，開展數學寫作研究也是對話教學的一種“課下對話”.具體地說，以上文提供的學生數學寫作為例，我們在批閱之后都及時給出了評析（有時也是賞析），這就是一種積極的師生對話方式，既肯定學生對錯題的理解角度與深度，又對其進行激勵、表揚，達到了鞏固知識、訓練技能、提振學習信心和激發興趣的多重功能.

三、寫在后面

最近幾年來，筆者一直開展學生數學寫作實踐研究，拍照、掃描收集存檔了大量學生數學寫作，多數常態化的學生數學寫作作品雖然達不到直接發表的標準，但是常常查閱會為學生數學寫作中偶爾有一兩句精彩的觀點而高興，并且會在后續教學中向學生推廣這些精彩的反思觀點或深刻的解題經驗，每每此時，那些被提及（引用）的學生就會非常興奮，覺得自己在數學寫作中某些觀點被老師引用，坐姿更加端正，聽課更加專注，課后有時又能提交一篇“文以載道”的優秀寫作.這事實上也激勵著我們持續開展這項“非功利”（看似與應試提分無直接聯系）的實踐研究，也期待有更多同行能充分利用數學寫作這種學習方式，促進學生的數學學習.