優選問題,挖掘本質
——基于深度思維的數學教學
☉四川省德陽外國語學校 顧有良
一、問題的提出
美國數學家哈爾莫斯說過:“問題是數學的心臟.”而思維源于問題,數學教學是一個數學思維活動的切入、分析、歸納與總結的過程,集中體現為提出問題、分析問題與解決問題的過程.因此數學教學必須從問題開始,以問題為載體,以問題的解決為中心,引發和指導學生的思維活動,真正調動起學生的全面思維,激發學生的深度思維,使其充分參與并揭示相關知識的發生過程、方法的形成過程以及問題的解決過程.這樣的數學教學一定能充分體驗到數學知識的美妙,培養出數學素養,步入數學幽境,真正使學生在數學教學的過程中優學、好學、樂學.
在數學教學過程中,針對數學課本、配套練習、課后練習、模擬試題、各類考試試題以及歷年高考真題等眾多的數學習題,以及各層面各類型的考試及其對應的試題,教師講不過來,學生也做不過來,那么在課堂上優選問題并展開討論,從而達到深度思維才是有效的課堂.
二、問題的分析
如何優選數學問題作為數學教學的媒介,是教師必須考慮的重點問題,特別是在高三復習階段,如何在較短的時間內進行有效復習與全面提升?優選問題就顯得更為重要.優選問題可以有效地節約時間,有針對性地進行講解與訓練,還可以在一定程度上保障深度思維的展開,從而得以真正有效地掌握知識,提升能力.
當然,作為數學教學過程中優選出來的典型問題,必須要具備典型性、代表性、知識性以及拓展性等相關的性質,通過講評優選出來的問題,既可以講清所要掌握的知識點,又可以與已有的知識加以有效聯系與復習,在一定程度上還可以進一步拓展與提升,從而真正達到深度思維,形成學生固定的知識體系與思維習慣,這才是最終的目的.
那么如何有選擇性地選取相應的數學問題,并進行針對性的數學教學,深化數學知識,拓展深度思維呢?
三、問題的解決
其實,可以進行有效的深度思維并優選出相應的數學問題主要存在于三個地方:課本中的例題與習題、各地有代表性的模擬題、歷年的高考真題等.當然,在具體的教學過程中,要有意識地加以積累,并有針對性地加以總結、歸類、反思、更新.
1.細選課本例題(習題)
數學教材中各部分的例(習)題具有典型性、代表性、示范性、遷移性與拓展性等特點,是幾代數學專家、學者集體智慧的結晶,歷經考驗.課本上一些例(習)題,看似平淡無奇,但都隱藏著深遠的背景,閃爍著智慧的光芒,有著意想不到的功能.因此通過細選這部分數學問題,在充分講解并深刻理解的基礎上,還要進一步拓展與提升,才能真正做到深化思維.
普通高中課程標準實驗教科書《數學·選修2-3·A版》(人民教育出版社,2009年4月第3版)第35頁探究與發現:“楊輝三角”中的一些秘密.
問題1:對于“楊輝三角”,探究與發現中給出4點規律.
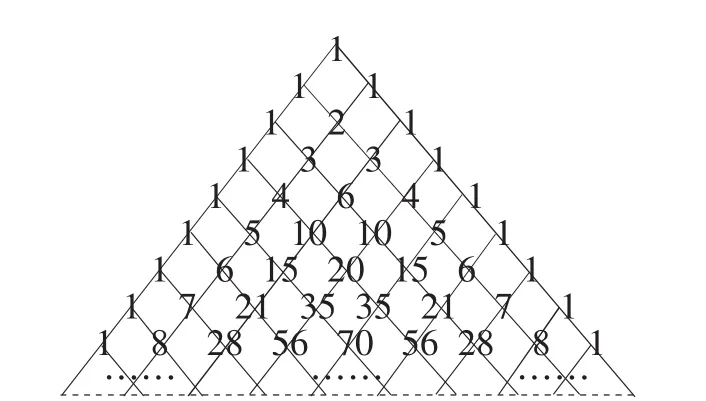
圖1
通過進一步拓展與探究,還能發現什么規律?這才是深度思維的進一步拓展與應用.
通過分析可以進一步歸納出眾多的規律,比如:(1)在楊輝三角中,第2n-1(n∈N)行的整行均為奇數;(2)在楊輝三角中,若第p行(n∈N)除1外,p整除其余的所有整數,則行數p是質數(素數);(3)在楊輝三角中,同一行中存在相鄰的三個數成等差數列所滿足的條件是:且k≥3)等等.
其實,借助“楊輝三角”,通過三角形數表形式,還可以拓展到其他類型的數表形式,其實質都是二項式定理、數列、函數、推理與證明等相關的數學知識的綜合與應用,充分體現了高考大綱對數學文化的展示以及創新應用,從而起到擴大知識面,提升能力,深化思維的目的.
2.優選高考模擬題
高考模擬題是一線教師與一線數學教研員們在一線教學過程中的體會、反思與總結,其中包括對課本知識的領會、高考大綱的理解、高考命題的剖析以及學生情況的反饋等眾多方面,具有極高的應用性.當然對高考模擬題要有針對性地選取,應選取相應教學時段所對應的問題,并加以合理應用與深化思維.
問題2:(2019屆江蘇省靖江高級中學高三12月月考)已知圓O:x2+y2=1,定點A(3,0),過A點的直線l與圓O相交于B,C兩點,B,C兩點均在x軸上方,如圖2,若OC平分∠AOB,則直線l的斜率為______.
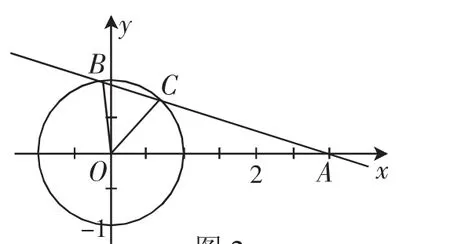
圖2
本題以解析幾何中的圓為問題背景,通過直線與圓的位置關系的建立,結合角平分線條件的介入,最終落到直線斜率的求解上.巧妙地把解析幾何、平面幾何加以交匯,把圓的方程、直線的方程、直線的斜率、角平分線等相關知識加以鏈接,進而達到知識交匯與能力拓展的目的.
常規思維方式——(交點法)結合角平分線定理的轉化得到|AC|=3|BC|,過點C作CD∥BO交x軸于點D,結合平行性質得到點C所在的圓并結合點C在圓x2+y2=1上確定點C的坐標,再利用直線的斜率公式求解即可.
解析:由于OC平分∠AOB,所以由角平分線定理可得,則知|AC|=3|BC|.

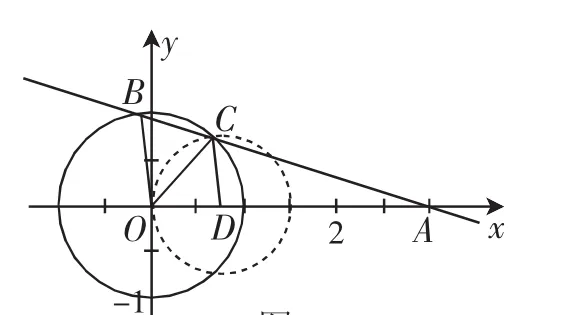
圖3
通過深度思維,可以與三角形面積加以結合,利用三角形面積轉化法來處理;也可以與角平分線定理加以結合,利用角平分線定理轉化法來處理;還可以直接回歸到坐標法,結合平面向量等相關知識來處理;又可以通過題目條件進行深度分析,并借助三角參數,利用三角參數法來巧妙解決.
優選高考模擬題,從一個簡單的基本問題入手,把解析幾何問題與平面幾何、平面向量、三角函數等相關知識加以有效整合,既拓廣了思維以及應用,又提升了能力,培養了素養.
四、感悟與反思
我們關注數學教學中的深度思維,本質上就是關注學生數學知識的構建效率與效度,這與數學課程標準這一根本目的完全吻合,也充分體現了數學核心素養.
因此,打造數學教學的深度思維,需要清晰明確的學習目的、起點與終點,通過數學問題的驅動,架起新舊知識間的橋梁,使得數學思維真正走上“高速公路”,達到深度思維,往廣處、深處等各個方面滲透、拓展.堅持這樣的數學教學,有意識滲透深度思維,那么有深度的數學課堂與數學教學就有可能實現,學生的數學知識有可能得以掌握,學生的數學核心素養有可能得以養成.

