例談注重“聯系”的高中數學公開課教學
☉浙江省臨海市大田中學 黃 柯
各級各類的公開課能夠有效地促進教師的專業成長,本文結合公開課教學的兩個方面談談公開課教學在促教促研上的巨大作用和意義,思考如何通過注重“聯系”的課堂教學引導學生在聯系中進行對比、分析與反思并最終生成智慧.
一、聯系“舊課”并探查教學深加工的空間
區域教研的目標之一就是讓教師以公開課為實踐園地來推動教學優化,承載著對教研主題進行實踐性詮釋任務的公開課教學是數學教學研討的基礎.因此,授課教師首先應該做的便是根據主題回顧“舊課”并對教學深加工的空間進行探查,實實在在地解決教學中的問題與困惑,然后推動教學優化.
案例1:兩角和與差的余弦.
教學片段1:促進認知
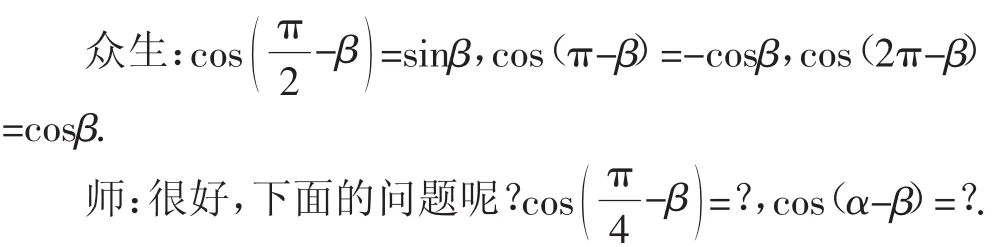
眾生:一臉困惑的表情.
師:看來這是一個新問題,那么大家能否對兩角差的余弦的一般結論進行猜想與表述呢?
學生給出了“cos(α-β)=cosα-cosβ”之類的猜想,用α和β的三角函數來表示cos(α-β)是主基調,筆者對學生的猜想及時進行了肯定并引導學生聯系反例對猜想進行了否定.學生雖然對具體的公式不甚明了,但卻表現出了極大的探究興趣.不僅如此,學生對cosθ能否用α和β的三角函數來表示也進行了思考,筆者及時作出了在單位圓中兩次計算任意兩單位向量的數量積的引導:在直角坐標系xOy中,以Ox軸為始邊分別作角α和角β并使其終邊分別與單位圓相交于A、B兩點,則A、B兩點的坐標如何?向量的坐標如何?假如把向量的夾角記作θ,大家是否能從向量的數量積定義與坐標表示來求得呢?
學生很快得出cosθ=cosαcosβ+sinαsinβ,問題也就轉化成了角θ、α、β之間關系的探究,這是一個一般性問題.
教學片段2:解決一般性問題
師:cosθ=cosαcosβ+sinαsinβ我們得到了,不過角θ、α、β之間的關系是怎樣呢?大家能否結合教材內容對這一問題進行初步的解決呢?
生1:畫出單位圓并設α=75°,β=15°,可得α-β=θ.
師:很好,從無“圓”到有“圓”的發現很不錯,不過大家對于θ、α、β之間的猜想有沒有錯呢?
生2:錯的,比如當α=15°,β=75°時,α-β=-θ.
師:換成其他特殊角會怎樣呢?比如α=80°,β=10°或α=10°,β=80°呢?
生3:角α、β的終邊狀態在實質上并沒有不同,因此仍有α-β=θ或α-β=-θ.
師:會不會是巧合?是否可以從終邊相同的角的集合的角度進行新的思考呢?是否有其他的可能?
生4:當α=370°,β=80°時,有α-β=360°-θ;當α=80°,β=370°時,有α-β=-360°+θ.
生5:還有α=440°,β=10°或α=10°,β=440°的情況,當α=440°,β=10°時,α-β=360°+θ;當α=10°,β=440°時,α-β=-360°-θ.
師:很好,大家能否從以上特殊化的探索中歸納猜想出角θ、α、β之間的關系呢?
生6:α-β=k·360°±θ,k∈Z.
師:很棒,你的猜想是對的,教材后面的習題也能使大家感受到這種一般化分類的方法,大家對于“余弦函數是周期為2π的偶函數”應該也能理解了,那么是不是只要考慮0≤α-β≤π這一種情況呢?
生7:誘導公式有cos(α-β)=cos(k·360°±θ)=cosθ,這是余弦函數周期性與奇偶性的反映,當0≤α-β≤π時,α-β即為向量的夾角θ.教材中表述的余弦函數是周期為2π的偶函數,且只需考慮0≤α-β≤π這一情況就是這個意思.
設計意圖:這是圍繞課程資源的教學交流活動,降低了提問的起點,且從方法論的角度上引導學生解決一般化問題的探究,并令學生在特殊化的探索中獲得了結論,課堂思維含量充足,恰到好處的課堂留白也讓學生活躍起來.
二、聯系“同課”并探查“異構”之處
不同教學思維的碰撞和對比往往能夠更好地發現“同”中的“異”,也能將教師對教材的不同理解與處理方法充分地展現出來.
案例2:兩角和與差的余弦.
王第成老師曾經就“兩角和與差的余弦”的教學做過思考,他的教學和案例1中的教學片段2在變換特殊量的“序”上并不相同.王第成老師的解決思路如下:根據向量的終點所在象限的不同,固定向量sin67°),(cos110°,sin110°),(cos260°,sin260°),這與案例1的教學片段2中的α-β=-θ、α-β=-360°+θ是相當的,這種隨意的特殊化往往容易令學生獲得錯誤的結論;依托課本內容的教學片段2從“隨意的特殊化”中發現了問題與可能的解決途徑,接著從α、β的大小以及終邊相同的角的集合的角度變換對應向量中的角來引導學生體會本質的“序”,順利建立“系統的特殊化”并歸納出一般化的結論:α-β=k·360°±θ,k∈Z.有學生在王第成老師的教學中這樣回答:不等于,不過由誘導公式可得到向量的夾角的余弦值與cos(α-β)是相等的.筆者認為,對于學生的這一回答,教師應作出以下引導:一定不等于?向量的夾角和α-β之間的關系是怎樣的?引導學生結合特殊向量來完善“隨意的特殊化”,并建立“系統的特殊化”,最終獲得一般化的結論:α-β=k·360°±θ,k∈Z.這也是讓學生看到了過程的補充化說明.
三、聯系“異課”并探究“同構”教學規律
教師對教材、教學設計、教學過程、學生活動等多個環節的有效反思與監控能令其課堂教學效果不斷提高,筆者曾認真考察過三位省級優課評比一等獎授課教師的課堂教學,三位老師的教學內容分別為數系的擴充、幾何概型和對數,筆者發現三位老師的授課內容雖然不同,但在學生活動的思維疑惑處設計問題是其共同的特點,不僅如此,數學史的融入也使三位老師的課堂更加富有感染力.下面對這三位老師的課堂教學作淺要的分析.
師1將學生熟悉的負數、分數、無理數等問題在解方程的環節中一一呈現,將數系的歷史發展規律在“做數學”中引入,使學生在回憶舊知的過程中獲得了數系的擴充規律與辦法.然后讓學生在面臨新問題時獲得認知沖突:接受還是不接受方程x2+1=0無解呢?實數不夠用的形勢必然需要數集的擴充.實數集的擴充是怎樣的呢?將意大利數學家卡爾丹解決“和為10的兩部分乘積等于40”的問題適時引入,令學生理解虛數產生的必要性的同時也理解了新數i的引入的合理性.
師2首先將法國數學家拉普拉斯的畫像進行了投影并口述了他的名言,在學生注意力都相當集中的時候以參賽抽簽為例進行了教學的過渡,和教材中的呈現不同的是,師2對剪繩子、射箭等概率問題還進行了整體分析并對不同于古典概型的特點進行了歸納整理,使學生在過渡中獲得認知沖突并對新問題的解決產生探究的欲望.課后對布豐試驗的表述又令學生的求知欲望再次得到激發,德育教育也在無形中得到了滲透.
師3所設計的客觀實際需求問題使學生在能夠感知并挑戰的數學活動中更加活躍,引發學生困惑與認知沖突的同時也令課堂教學活動更為生動.
問題一:光在某種介質中每經過1cm即會在強度上減弱成原來的一半,若最初的強度為1.
(1)經過2cm后的強度是多少?
(2)經過xcm后的強度y是多少?
(3)強度是0.125時,光經過了多少cm?
問題二:方程有解嗎?等于多少?
師:大家認為這個方程有解嗎?是不是唯一的?
生:根據指數函數的圖像可以說明它是有解的,如圖1,解為在函數中和函數值相對應的自變量x的值.
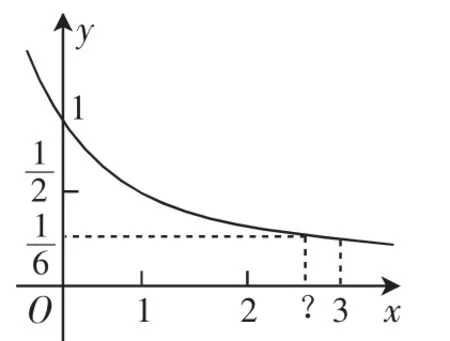
圖1
師:很好,確實如此,有解且唯一.我們用以前學的知識根本求不出這個解,大家以前遇到過這樣的困境嗎?
師3及時給出了“分數問題”“平方根問題”并引導學生對前人發現的歷史進行了追溯,這是為對數的生成所做的鋪墊.不僅如此,師3在學生發現需要新的符號來表的解時又及時進行了跟進:太棒了,指所確定的,這種新形式的“數”早在400年以前便被創造出來,其創造者是蘇格蘭數學家納皮爾.解決指數運算困境的同時所融入的數學史教育令學生對數學文化的價值再添印象.
總之,教師在公開課的設計與教學中應經歷問題的確認、想法的形成、教學的設計、課堂的觀察以及課后的評價反思等環節,這也是發展教育理解力、批判力、建構力的豐厚土壤.W

