基于“學歷案”的數學微專題設計*

☉浙江省象山縣第二中學 呂增鋒

最近，我縣舉行了“數學微專題設計”的評比活動，筆者有幸擔任評委.數學“微專題”是指圍繞重點和關鍵點設計的、利用具有緊密相關性的知識或方法形成的專項研究，或者結合學生的疑點和易錯點整合的、能夠在短時間內專門解惑的問題集.與一般的大專題教學相比，微專題教學具有“因微而準、因微而細、因微而深”的優點.

一、“微專題”設計有缺陷

本次“微專題”設計的主題是“函數綜合問題的解法探究”，面向的學習對象是高三學生.為了適應高三復習課的需求，所有參賽教師均以“例題+練習”的方式來設計“微專題”.下面是比較有代表性的一個設計案例：

【主題】含參數方程有解的取值范圍問題

【例題分析】例1設關于x的方程x2-ax-2=0和x2-x-1-a=0的實根分別為x1，x2和x3，x4，若x1＜x3＜x2＜x4，則實數a的取值范圍是______.

【鞏固練習】

（1）已知函數f（x）=x2-2ax+a+2|x2-1|在區間（0，3）上有兩個零點則實數a的取值范圍是______.

（2）已知函數f（x）=|x3+1|x，x∈R，若方程f（x）-a|x-1|=0恰有4個互異的實數根，則實數a的取值范圍為______.

（3）已知函數f（x）=|x2-2|+x2+ax在區間（0，2）上有兩個零點，則實數a的取值范圍是______.

上述的案例體現了“微專題”“小切口，深挖掘”的設計理念，對教學的難點起到了有效地突破.但我們也發現這樣的微專題與常見的練習或者復習資料沒什么區別，無非是問題更具針對性，例題數量減少了，在教學中還是難以擺脫“教師講，學生聽”的枷鎖，學生的學習方式根本沒有得到任何改變.不僅如此，上述例題數量雖少，但難度很高，思維跨度較大，如果沒有鋪墊式的問題設計，那么學生直接面對如此復雜的問題情境恐怕在教學成效上會大打折扣.那么，如何彌補微專題的這些缺憾呢？

二、何為“學歷案”

“學歷案”是由華東師范大學崔允漷教授首先提出的.“學歷案”指的是教師在班級教學背景下，圍繞一個具體的學習單位，從期望“學會什么”出發，設計并展示“學生何以學會”的過程，以便于學生自主構建經驗或知識的專業方案［1］.“學歷案”運用建構主義方法，將教學內容的目標、任務、方法、資源、作業、互動、評價與反思等要素優化組合為一個教學系統，呈現學習的完整歷程，形成完善的知識結構.具體組成要素如下表所示［2］：

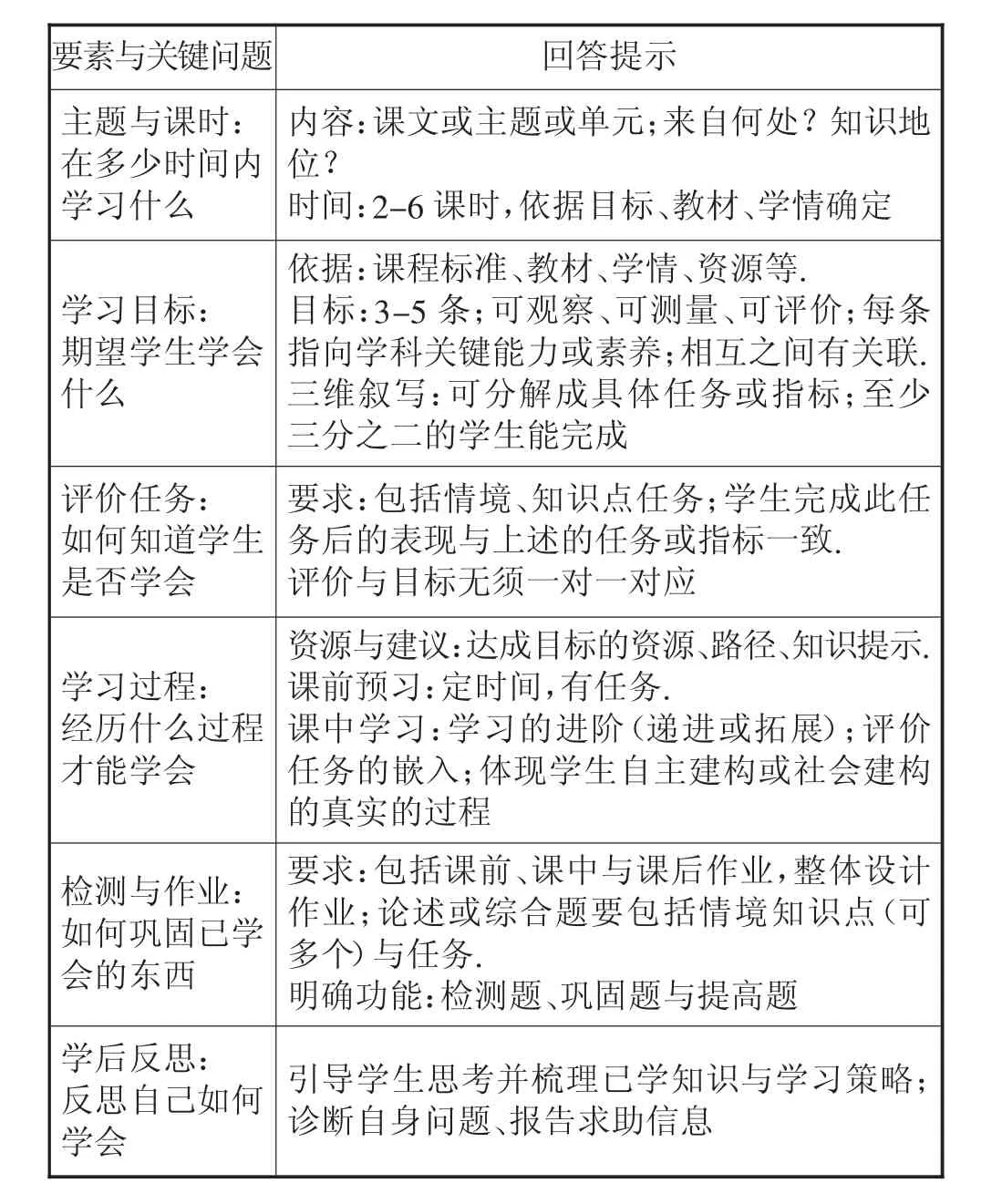
要素與關鍵問題 回答提示主題與課時：在多少時間內學習什么內容：課文或主題或單元；來自何處？知識地位？時間：2-6課時，依據目標、教材、學情確定學習目標：期望學生學會什么依據：課程標準、教材、學情、資源等.目標：3-5條；可觀察、可測量、可評價；每條指向學科關鍵能力或素養；相互之間有關聯.三維敘寫：可分解成具體任務或指標；至少三分之二的學生能完成評價任務：如何知道學生是否學會要求：包括情境、知識點任務；學生完成此任務后的表現與上述的任務或指標一致.評價與目標無須一對一對應學習過程：經歷什么過程才能學會資源與建議：達成目標的資源、路徑、知識提示.課前預習：定時間，有任務.課中學習：學習的進階（遞進或拓展）；評價任務的嵌入；體現學生自主建構或社會建構的真實的過程檢測與作業：如何鞏固已學會的東西要求：包括課前、課中與課后作業，整體設計作業；論述或綜合題要包括情境知識點（可多個）與任務.明確功能：檢測題、鞏固題與提高題學后反思：反思自己如何學會引導學生思考并梳理已學知識與學習策略；診斷自身問題、報告求助信息

三、基于“學歷案”的“微專題”設計

“學歷案”的編制需要思考學生學什么、怎么學、學到什么程度等問題，從學習內容的確定到期望學生實現的目標的表述，再到達成目標的教學活動的安排，最終到檢測目標實現與否及其掌握程度的課內評價設置，整個學習流程清楚明確，保障學生“在”學習，經歷“真”學習.

1.學習目標

學歷案中的學習目標要指明在學習過程中，學生將要獲得什么、如何獲得以及掌握到什么程度.學習目標必須包含四個要素：行為主體、行為動詞、行為條件和行為標準，即誰來學、學什么、在什么條件下學、學到什么程度，四個要素缺一不可.因此，在“微專題”的設計中，首先考慮的不是例題的選取，而是學習目標的制定.針對“含參數方程有解的取值范圍問題”這個微專題，學習目標可以這樣制定：

（1）通過具體的問題，梳理方程的根、函數零點、圖像交點之間的關系，根據問題的要求能夠對根、零點、交點進行靈活轉化；

（2）經歷方程轉化為函數的思維過程，結合具體問題，靈活構建函數，能夠借助圖像的直觀性來解決抽象的數學問題；

（3）經歷從簡單到復雜的思維過程，感受方程的根轉化為函數的零點或圖像的交點對于簡化運算的意義，體會數形結合思想在解題中的應用，發展數學抽象、數學運算、直觀想象等核心素養.

相對于課程標準中教學目標的表述，“學歷案”中教學目標的表述更加具體化、策略化，更加具有可操作性.

2.評價任務

“學歷案”關注的是學習目標的達成，因此它遵循的是一種逆向設計路徑，即“學習目標——評價任務——學習過程”.“評價任務”的設計優先于“學習過程”的好處是有助于教師厘清目標達成的“標準”以及正確區分學習任務與評價任務，唯有這樣才能保證“學——教——評”的一致性與系統性［3］.

“含參數方程有解的取值范圍問題”的評價任務如下：

（1）完成問題1，回答思考1、思考2、思考3，完成練習1；

（2）通過提示，解答例1，完成練習2；

（3）通過合作學習，解決例2，回答思考4、思考5，完成練習3.

3.學習過程

“學歷案”遵循的是“以學為中心”的理念，它呈現的是一個完整的自主學習過程，因此，學習過程的設計應該立足于學生已有的經驗與思維邏輯，通過問題驅動的方式循序漸進，層層深入，進而充分展示數學知識的發生以及發展的過程，讓學生成為知識的主動建構者.“含參數方程有解的取值范圍問題”微專題的學習過程可以這樣設計：

第一部分：探索根、零點、交點之間的關系問題：關于x的方程x2-ax-2=0在R上有根，則實數a的取值范圍是______.

思考1：上述問題有幾種解題思路，請把解答過程寫出來.

思考2：方程的根、函數的零點、圖像的交點之間存在著什么關系？

思考3：你認為對于這樣的問題，哪種解題思路更為簡單？

練習1：關于x的方程x2-x-1-a=0在x∈［0，1］上有實根，則實數a的取值范圍是______.

意圖：一方面，通過問題的解答梳理根、零點、交點之間的關系，掌握必要的基礎知識；另一方面，初步體會把方程的根的問題轉化函數的零點、圖像的交點的好處，掌握基本的變形、轉化、構造等技巧.

第二部分：解題技巧的探究

例1 設關于x的方程x2-ax-2=0和x2-x-1-a=0的實根分別為x1，x2和x3，x4，若x1＜x3＜x2＜x4，則a的取值范圍是______.

解題視角一：轉化為函數的零點

提示1：把兩個方程直接轉化為函數，畫出滿足上述條件的兩個函數的圖像.

提示2：觀察并分析圖像，列出滿足條件的代數式.解題視角二：轉化為圖像的交點

提示1：通過變形，把每個方程轉化為兩個函數圖像的交點.

提示2：畫出滿足條件的圖像，觀察交點的分布，列出相關的代數式.

練習2：已知函數f（x）=x2-2ax+a+2|x2-1|在區間（0，3）上有兩個零點，則實數a的取值范圍是______.

意圖：明確解題的視角，通過設置必要的提示，降低問題的難度，以啟迪學生思維.

第三部分：解題技巧的進一步提煉

思考4：比較此題與例1的差異？

思考5：根據什么標準來構造函數？

練習3：已知函數f（x）=|x2-2|+x2+ax在區間（0，2）上有兩個零點，則實數a的取值范圍是______.

意圖：類比例1的解題思路，掌握函數構造的一般技巧，進一步提煉解題策略.

學習過程的設計采用“師留白，生留痕”的策略，將學習的主動權、創造權還給學生，從而使課堂變得充滿靈性.

4.學后反思

“學后反思”是學歷案的重要組成部分，其要求學生在課后完成一個復雜的筆紙任務，包括對知識和學習策略的梳理，診斷自身問題，總結值得分享的觀點或成果，發出求助信息等.“學后反思”一方面是學生自主學習的延續，另一方面有助于學生養成反思習慣，并主動汲取學習經驗，從而提高自身的原認知水平.

對于“含參數方程有解的取值范圍問題”微專題的學習反思可以引導學生圍繞著以下幾方面進行：

（1）構造函數遵循的原則（如：一靜一動，一直一曲）

（2）此類問題的解題策略（如：構造函數，動態分析，考慮臨界狀態）

（3）類似試題的整理

（4）你還存在著哪些困惑

相對于“例題+練習”微專題的“粗放”設計，基于“學歷案”的微專題設計就顯得非常精致，其更加關注學生的學習體驗.學生只需按照“學歷案”設計的學習流程就能夠順利實現自主學習，從而實現“以教師講解”為核心的傳統高三復習課向“以學生學習”為中心的生本課堂的轉變.