思維在交流中提升 素養在探究中發展
——一道解析幾何模考題的多視角探求與思考

☉江蘇省通州高級中學 嚴振君

解析幾何是高中數學課程的核心內容，是高考考查的重點內容，是諸多數學思想方法的交匯點．解析幾何的教學承載著發展學生直觀想象、數學抽象、數學運算、邏輯推理和數學建模等數學學科核心素養的功能．如何提升學生解析幾何的思維能力，發展學生的數學核心素養，是一線教師應該思考與研究的問題．筆者以一道解析幾何模考題的多視角探求的課堂教學為例，談談在解析幾何的解題教學上的些許思考．

一、原題呈現

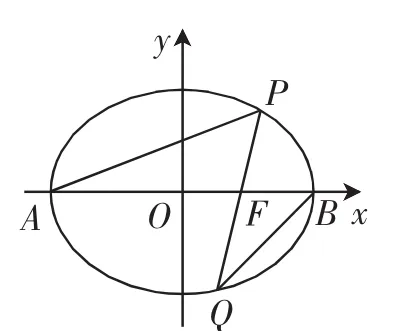
圖1

（1）若QF＝2FP，求直線l的方程；

（2）設直線AP，BQ的斜率分別為k1，k2．是否存在常數λ，使得k1＝λk2？若存在，求出λ的值；若不存在，請說明理由．

二、基本情況

第（2）問的作答情況不太理想，主要體現在：審題欠深入，未能深刻挖掘題意；思路受局限，處理手段相對匱乏；計算能力差，解題半途而廢．

筆者執教的是四星級重點高中物生組合班，學生基礎較好，運算求解、邏輯推理等能力均具備一定水平．在日常教學中，筆者較好地貫徹了當地教育部門所倡導的“限時講授、踴躍展示、交流合作”12字課堂教學指導方針，并且讓學生能夠積極展開小組交流，踴躍展示研究成果，課堂氣氛十分活躍．

考慮到受考試時間等多重因素的影響，學生未能對第（2）問展開深入思考，故課前再留給學生一定的獨立思考的時間，并結合批閱情況，對本題實施“一題一課”的教學嘗試．

三、教學過程

1.解法探討，思維在交流中提升

視角1 直譯題意 順勢而下

師：本節課我們重點研究第（2）問，請生1闡述對題意的理解，并展示解題過程．（學生投影解題過程，同時講解，本文摘錄其部分解答過程.）

生1：假設存在常數λ，使得k1＝λk2，利用題設中已知直線AP的斜率為k1，設直線AP的方程與橢圓方程聯立，求得由假設k1＝λk2，得，又因點P，F，Q三點共線，故kPF=kQF，即，整理得

即（4λk22+3）（3λ-1）=0，則

師：生1書寫清晰工整，過程詳細規范，值得大家學習．那么是否存在思維或表達不夠嚴謹的地方？

生3：實際需對直線l斜率不存在的情形予以驗證．生1對（4λk22+3）（3λ-1）=0的處理過于草率，應理解成：對任意直線BQ，即k2恒成立．

師：解題時要注意思維的嚴謹性．是否有同學就此解法提出不同的處理方式？

視角2 設而不求 各顯神通

師：上述解法均是借助題設中已有直線的斜率k1，k2進行解題.生4指出本題目的實為尋求斜率k1和k2的關系，因而直接構建k1，k2的等式.還有不同的想法嗎？

師：你是怎么想到的？從哪里得到啟發？

生5：首先，根據“過右焦點F的直線l與橢圓C交于P，Q兩點”的表述，感覺可以從直線l入手；其次，解析幾何中“設而不求”是常規套路，理應嘗試；再次，生1的解法的思維路線圖為：，根據經驗，可從③切入，逆向而行.

師：理解題意不能僅停留在文字表述層面上，應深刻挖掘題意.利用思維路線圖探尋思路是解題的常規策略.但選擇此法的同學遇到了一個“棘手”的問題.

師：對該目標式應如何處理？

生7：為什么不可以？我就是這么做的！

生7的突然質疑打斷了其他同學的思緒，并且迫不及待地展示出解題過程：不妨取我在解題過程中保留了這個整體，計算過程并不復雜.

此時其他同學報以熱烈的掌聲，無一不被生7“敢算”的信念和“會算”的技巧所折服.

師：此法“簡單粗暴”但作用明顯.我們還得冷靜思考，“暴力求解”的做法與“設而不求”的初衷似乎有所背離，可以“設而不求”嗎？對于兩根“不對稱”的情形，是否可以轉化為兩根“對稱”的情形呢？

學生又一次陷入沉思，大概兩分鐘之后，有學生提出自己的想法.

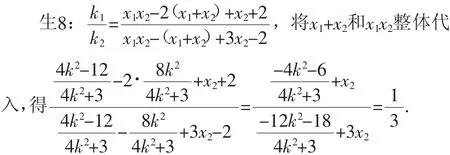
師：對于該目標式，同學們嘗試過其他處理方法嗎？

學生面露難色，或演算，或思考，一籌莫展，筆者適時予以提示.

師：剛才利用的是點P、Q都在直線l上統一同一點的橫、縱坐標，有無其他統一橫、縱坐標的辦法？

生10洋洋得意，其他同學投來羨慕的目光.與此同時生10也不忘總結：應充分關注交點P，Q的雙重身份，在拋物線中不是經常利用點在拋物線上嗎？鑒于橢圓方程中x、y是雙隱性的，因此對目標平方就變得理所當然和勢在必行.其他同學恍然大悟，此時生11躍躍欲試.

生11：由題意，直線l的斜率不為0，設直線l：x=my+1，代入橢圓方程，得（4+3m2）y2+6my-9=0，則y1+y2=兩式相比得

生11：直線l過焦點F（1，0），設l為x＝my＋1的形式，一則避免了討論斜率不存在的情形，二則運算得以簡化，三則思路變得更為順暢，相對于設直線l：y=k（x-1）的形式優勢明顯．

面對如此簡潔明了的解題過程，同學們表示驚嘆．隨著課堂教學的不斷深入，同學們思如泉涌，爭先恐后，意欲展示自己的想法．

視角3 打破平衡 設點求點

解析幾何的課堂教學永遠是“累”的，除了要構思出合理的解題路徑外，復雜繁瑣的計算也必不可少．課時已過大半，學生看我絲毫沒有結束此題講解的意思，都提起了精神．

師：生11提醒我們方法的選擇和計算的繁簡也是密切相關的．剛才我們集中精力在如何求證k1∶k2為定值上，那么我們繼續思考，還有其他突破口嗎？也可以將自己不成熟的想法提出來，大家共同探討．

生12：我的出發點也是生1的思維路線圖．我打破此路線圖的平衡，抓住了點P、Q的一一對應關系，從直線PF入手，設點求點．在解題時，往往會形成初步的思維路線圖，再嘗試從圖中的不同環節尋求突破口，評估優劣后，擇優而從．此法具有一定的通性，盡管初用時計算較繁瑣，但熟練掌握后五分鐘之內便可完成．

視角4 定值問題 先猜后證

生13：本題初看是“存在性”問題，實則是“定值”問題，因此嘗試“先猜后證”的策略．當直線l的斜率不存在時，可得．由題意可知，λ若存在則必為，下恒成立即可．設直線l：x＝my＋1由（見生11解題過程），可得于任意m恒成立．

視角5 善用結論 巧妙擊破

當筆者欲對本題進行總結，留時間給學生整理思路和方法，并讓學生重新計算時，生14提出了新的想法．

生14：與生5的想法一樣，但“非對稱”的目標難處理，如何轉化是關鍵．聯想到橢圓的第三定義：已知kPA·kPB為定值，要求是定值，即求kPB·kQB為定值.因為k2kPB=

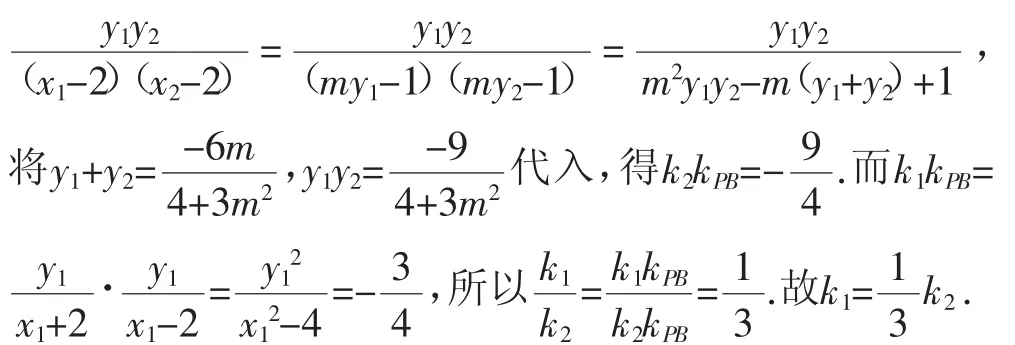
教室里響起了熱烈的掌聲，同學們向生14投來贊許的目光．

看著同學們沉浸在從多個視角探求到各種解法的喜悅中，筆者抓緊追問：本節課我們從5個視角探求了本題的若干個解法．請同學們思考，本題的多種解法是偶然還是必然？通過對解法的探求有哪些收獲？能否將本題結論拓展至更一般的情形？

2.拓展延伸，素養在探究中發展

為了使同學們能夠互通有無，加深對題目的不同視角、不同方法的理解，筆者照常組織學生進行小組活動，并匯報探究成果．

小組1：要深刻理解題意，提取題設中的關鍵信息，善于從不同視角思考和解決問題．思維路線圖在尋求解題思路時起著舉足輕重的作用．從思維路線圖的不同環節切入，解題的可行性和復雜性以及計算的難易程度會相去甚遠．

小組2：生14的解法揭示了本題的本質，由于kPA·kPB均為定值，可確保是定值．

師：課后請同學們對本題不同視角的各種解法繼續梳理，融會貫通，并將計算進行到底．對小組3提出的一般性結論予以完善并證明．

四、教后反思

解析幾何教學中，要著力激發學生積極思考，引導學生將問題拓展，融會貫通，提升思維 能力，提高思維品質，增強解題效率，從而促進數學學科核心素養的發展．

現如今師生在課堂中通過互動生成知識的比重日益提升，如何實現師生多向且高效的互動是新的研究話題．新課標指出“教師要把教學活動的重心放在促進學生學會學習上，積極探索有利于促進學生學習的多樣化教學方式”“．一題一課”具備自主、探究、開放、多元等特征，“限時講授、踴躍展示、交流合作”的課堂教學模式，讓學生變為主體，教師成為組織者、引導者、參與者，從典型的核心問題出發，“借題發揮”，通過鋪墊、類比、聯想、變式、延伸等途徑，引導學生獨立思考，并自主探究問題規律，完善認知結構，遞進思維層次，提升思維能力，達到“研一題，懂一類，通一片”的教學效果，實現課堂教學的本真高效．