善抓要點提思維 活化方法升素養
——淺議《數學歸納法》的教學

☉江蘇省金湖中學 陳萬斌

數學素養是指學生通過數學知識和方法的積累與掌握、運用與內化，在實際情境中經歷從數學的角度思考問題，用數學思想分析問題，用數學方法解決問題，進而形成的能力、習慣和品質等.數學核心素養是指數學學習者應具備的適應終身發展和社會發展需要的必備的數學品格和數學關鍵能力，是學生學習數學所應達成的有特定意義的一種綜合性能力，應當在教與學的過程中引起教師與學生的關注.數學核心素養是以數學知識與技能為基礎，以運用數學知識與技能解決問題為表現形式，數學本質的把握與相關的數學思想是在數學學習的過程中形成的.而通過對數學歸納法這一內容的學習，就能極大的提高思維能力，從而提升數學素養.

數學歸納法是高中階段的一種重要的證明方法，用來解決與自然數“n”有關的問題，有著其他證明方法不可替代的作用.學會數學歸納法，不僅要解決相關的數學問題，還要通過解決問題，來深化對數學歸納法內涵的理解，不是套用兩個機械的步驟，而是充分利用“有限”的手段來解決“無限”的問題；掌握運用數學歸納法解題的基本要點和注意事項；加深數學歸納法與其他知識和方法的聯系，從而提高解決問題的綜合能力；同時會靈活運用數學歸納法，不能固化；更重要的是通過對數學歸納法的學習和運用，強化數學歸納法的數學本質，培養學生的邏輯思維能力，提高學生善于聯系、擅長邏輯推理的核心素養.

一、掌握歸納法要點

（一）注意兩個步驟

1.確定初始值n0

例題1比較2n與n2的大小并證明.

解析：當n=1時，2n＞n2，當n=2時，2n=n2，當n=3時，2n＜n2，當n=4時，2n=n2.

猜測：當n≥5時，2n＞n2.

證明：（1）當n=5時，25＞52，不等式成立.

（2）假設當n=k（k≥5）時，不等式成立，即2k＞k2.

則當n=k+1時，2k+1=2·2k＞2·k2. 因為2k2-（k+1）2=k2-2k-1=k（k-2）-1＞0，

所以2k+1＞（k+1）2，故不等式也成立.

所以由（1）（2）可知：當n≥5時，2n＞n2.

評議：從數值比較中確定初始值，進而找到數學歸納法“遞推的基礎”.

2.觀察“項”的變化

評議：從“n=k”到“n=k+1”時要注意差異性，即“項”的變化，進而推導出數學歸納法“遞推的根據”.

3.探尋兩步驟聯系

（1）尋找遞推的關系

例題3…（1+nx）（其中n∈N*且n≥2），其展開后含xr項的系數為

（2）設a2=h（n），a1=g（n），求證：h（n）

解析：（1）易知：a1=1+2+…

h（n+1）=h（n）+（n+1）g（n）.

證明：①當n=2時，a2=2，而h（2）=

所以等式成立.

由①②可知：等式得證.

評議：第二步的“假設”本身就是一個“證明”.

（2）尋覓數式結合的橋梁

例題4已知數列{an}滿足的通項公式，并證明.

解析：可以利用特殊值運算后猜測an=2n.

證明：①當n=1，a1=1+1=2，猜想成立.

②假設當n=k時，猜想成立，即ak=2k.

所以ak+1=2ak=2×2k=2k+1，所以當n=k+1時等式也成立.

由①②知：an=2n，n∈N*.

評議：抓住“假設”對數式進行“分解與組合”.

（3）尋求內在的規律

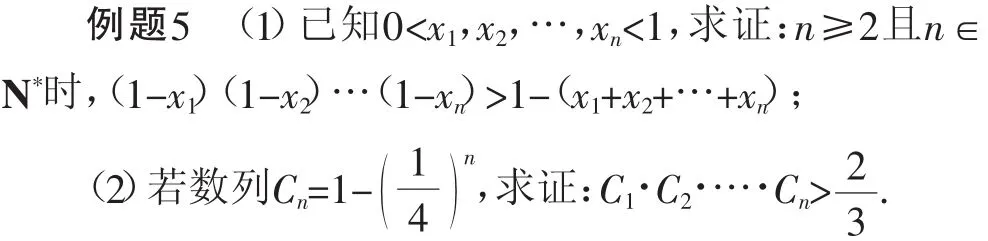
證明：（1）①當n=2時，因為0＜x1，x2＜1，則（1-x1）（1-

②假設n=k（k≥2）時，結論成立.

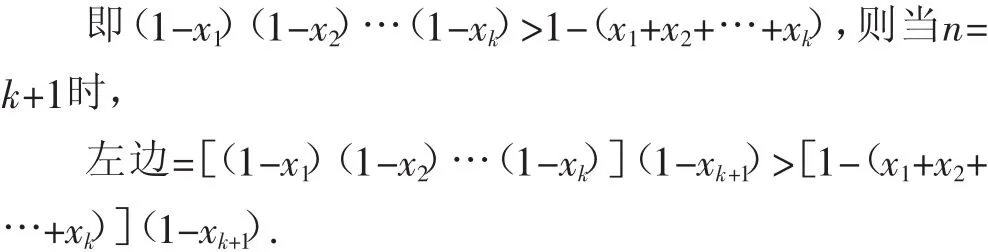
由①的“證明規律”可知：

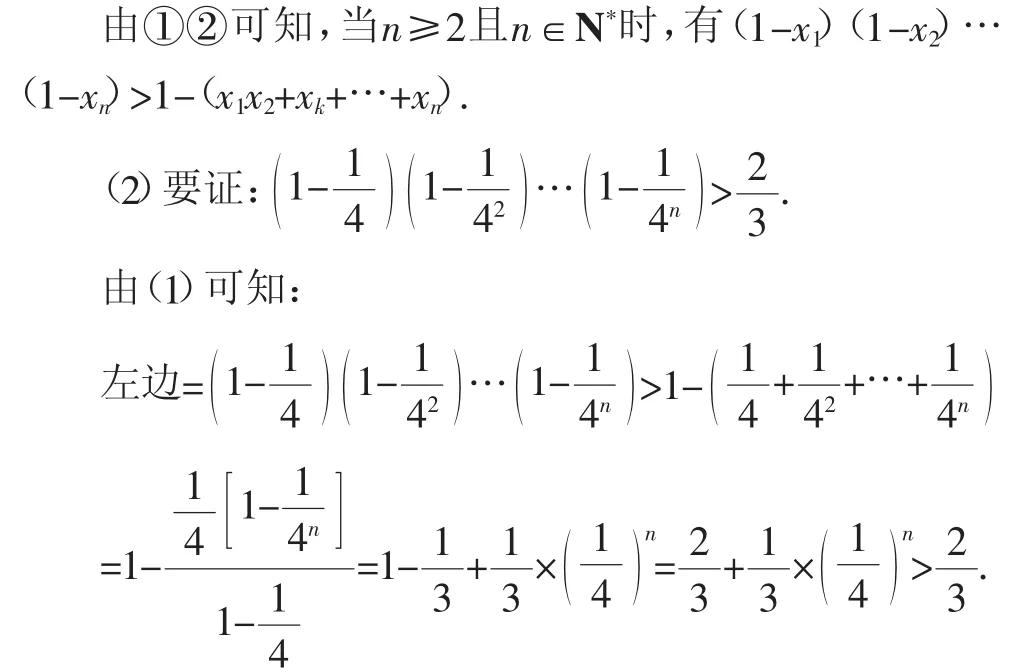
所以原題得證.

評議：通過第（1）問的證明發現內在隱含的關系或規律，再將其用于第（2）問.

（二）注意二次證明

例題6求證（3n+1）·7n-1能被9整除（n∈N*）.

解析：預備證明7n+2能被3整除（數學歸納法證明，證明略）.

本題證明：設Dn=（3n+1）·7n-1，

（1）當n=1時，D1=4×7-1=27=3×9，結論成立.

（2）假設n=k時，結論成立.

即Dk=（3k+1）·7k-1是9的倍數，

則當n=k+1時，

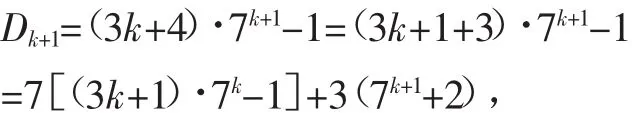
由假設及預備證明可知Dk+1＝7ak+3（7k+1+2）也是9的倍數，所以結論也成立.

由（1）（2）知：對?n∈N*，（3n+1）·7n-1能被9整除.

評議：有時需要二次證明，即“預備”證明.

二、學會歸納法拓展

例題7已知x+x-1=2cosθ，求證：xn+x-n=2cosnθ（n∈N*）.

證明：（1）當n=1時，等式成立.

當n=2時，x2+x-2=（x+x-1）2-2=（2cosθ）2-2=2cos2θ，所以等式成立.

（2）假設當n≤k時，等式成立.

即xk+x-k=2coskθ，xk-1+x-（k-1）=2cos（k-1）θ，

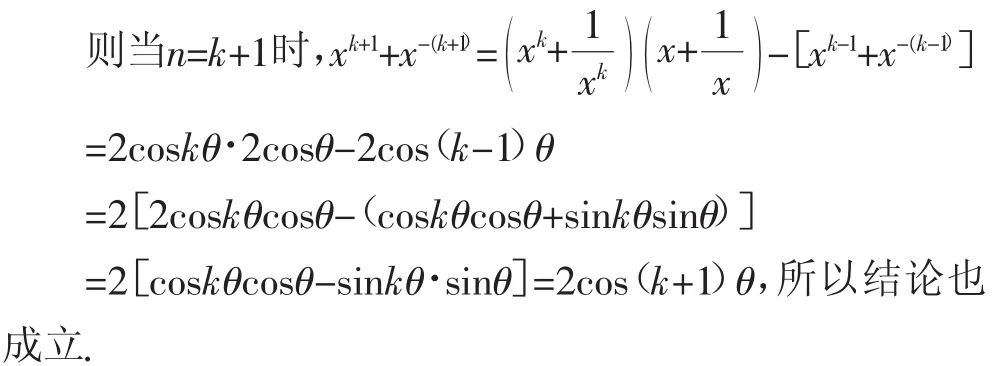
所以由（1）（2）可知：xn+x-n=2cosnθ.

評議：對數學歸納法的拓展，俗稱“第二數學歸納法”.

三、開展多角度聯想

（一）與函數有關

例題8對任意x＞1，n∈N*，求證

證明：（1）當n=1時，只需證ex-1＞x.設F（x）=ex-1-x（x＞1），則F（1）=0.又x＞1時，F ′（x）=ex-1-1＞0，所以F（x）是（1，+∞）上的增函數.故當x＞1時，即有F（x）＞0，則ex-1＞x結論成立.

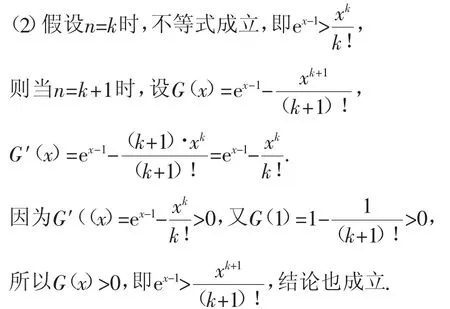
由（1）（2）可知：原題得證.

評議：建構函數，利用函數本身的性質.

（二）與二項展開式有關

例題9已知n≥2且n∈N*，比較（n+1）n與2n·n！的大小.

證明：（1）當n=2時，a2＞b2，不等式成立.

（2）假設當n=k（k≥2）時，不等式成立，ak＞bk，即

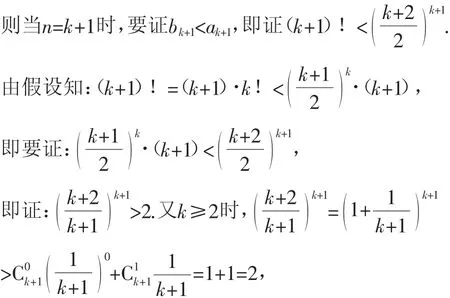
所以bk+1＜ak+1，則不等式也成立.

由（1）（2）可知：當n≥2且n∈N*時，（n+1）n＞2n·n！.

評議：掌握證明過程中的知識交匯、方法交叉和交融.

數學歸納法雖然只有兩個步驟，只是解決與自然數“n”有關的命題，看似形式簡單、步驟機械、應用面狹窄，其實不然.其一數學歸納法本身格式嚴謹、內涵豐富，理解數學歸納法需要感悟并深化其本質；另外數學歸納法的步驟二本身就是一個“證明”，要求學生善于運用“假設”；其二數學歸納法應用廣泛，方法獨特；其三數學歸納法與其他知識、方法聯系密切，知識和方法的交叉能極大地提高學生的想象能力，培養學生的發散思維.通過教師的積極引導、學生的反思，不僅使學生掌握數學歸納法的基本步驟、基本要領、基本應用，而且能進行靈活地運用，特別是學會分析問題并能解決問題，更重要的是在學習過程中提高了學生的邏輯推理能力和善于聯想的意識，數學素養也因此得到了很大的提高，這才是學習數學知識的最終目的.W