把握主線類比探究，歸納性質素養提升

尤方成

[摘 ?要] “不等式的性質”是學生學習有理數大小比較、等式、數軸等基礎上的知識深化，在教學設計時需要把握大綱要求，結合教學重點設計主線，采用合理的方式完成新知教授. 文章將深入分析“不等式的性質”內容，開展教學環節的設計探討與反思.

[關鍵詞] 不等式;性質;類比;應用

“不等式的性質”是初中數學七年級下冊的重要教學內容，其中的性質定理是基本數量關系學習的基礎，也為后續的解不等式和不等式組的解集提供了理論依據，因此該部分內容具有極高的教學意義，下面對其內容及環節設計進行探討.

關于教學內容的分析

《課程標準》明確指出要求結合實例引導學生自主探索不等式的基本性質，深刻認識不等式的三條基本性質，并能準確利用性質來解決現實問題，同時學習其中的數學語言，培養學生的核心素養. 上述內容對“不等式的性質”的教學提出了兩方面的要求：一是使學生掌握性質，二是培養學生的核心素養，尤其是語言能力. 基于該內容，結合學生的認知能力提出以下幾點思路建議：

1.不等式的性質教學需要采用探究式的教學方式，使學生經歷知識的探究過程，自主總結形成性質，提升學生的探究能力.

2.不等式與數軸之間有著一定的關聯，教學時需要采用類比的方式，通過數形結合的方式強化學生對定理的認識.

3.不等式性質的學習是為了解決問題，在完成性質總結后有必要開展性質的應用探究，通過對具體問題的分析來提升學生的應用能力.

關于教學環節的設計

基于上述的內容分析，在教學“不等式的性質”時需要考慮知識探究、類比教學、語言強化、性質應用等幾個關鍵點，因此教學中可以按照“情景引入—類比探究—語言強化—拓展應用”的教學主線，完成不等式的“現實抽象→性質總結→知識應用”的過渡轉換. 下面基于教學主線思考環節設計.

設計環節（一）——情景設計，課題引出

在生活中存在眾多的不等式問題及現象，因此設計具體的活動，從中抽象不等式更能提高學生的學習熱情，同時使學生深刻感受“知識源于生活”的內涵，可以設計如下情景活動.

情景活動：課前請大家準備一個圓和正方形紙板，如果我們知道兩個紙板的周長均為l，思考如何比較圓形和正方形的面積大小.

引問1：圓的半徑和正方形的邊長分別是多少？

引問2：圓和正方形的面積如何表示？

引問3：結合經驗可判斷出兩者的面積哪個大？

引問4：除了利用分數知識外，還有哪些方法來解釋？

教學中首先引導學生利用圖形的周長和面積公式構建相應的模型，即周長為l時，圓的面積為，而正方形的面積為. 然后結合知識經驗“周長相等時，圓的面積最大”學生可以判斷出圓的面積大于正方形的面積，即>. 此時需要教師進一步引導學生思考如何解釋這一結論，在之前學生已經掌握了分數的相關知識，能夠通過比較分母的大小來得出結論，課題引入時只需要讓學生思考還有哪些方法解釋結論即可.

設計環節（二）——類比研究，認識符號

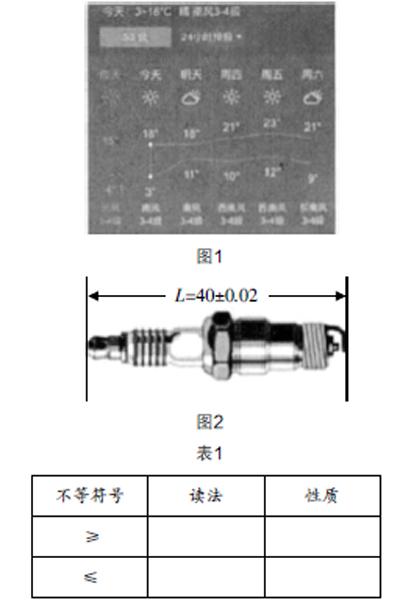
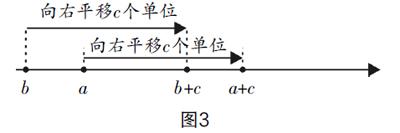
不等式性質學習的基礎是對不等式的符號有著充分的認識，因此在探究性質前需要類比認識不等符號“≥”和“≤”. 首先給出溫度圖（圖1）和零件設計圖（圖2），使學生嘗試使用不等符號來表示溫度的變化范圍和零件的合格尺寸. 然后在此基礎上引導學生思考不等符號所具有的類似性質，完成表1的填寫.

類比溫度變化和尺寸表示，學生可以較為直觀地認識不等式的符號，并對其性質意義有一個初步的了解，從而完成不等式符號的語言學習.

設計環節（三）——類比探究，性質學習

不等式的三大性質是本章節教學的重點，也是難點所在. 考慮到其性質較為抽象，在探究過程中可以充分把握不等式與等式之間的關聯，類比學習完成不等式性質的歸納，同時利用數軸的直觀性來完成性質的驗證.

類比活動：完成表2的填寫.

在教學中設計如上填表活動，學生通過數的大小比較很容易就可以發現其中隱含的規律，此時教師就可以引導學生對其加以歸納，并用文字語言概括. 考慮到上述性質是類比總結所得，因此教學中十分有必要對結論進行驗證.

1. 性質1驗證

對于性質1——不等式兩邊加（或減）同一個數（或式子），不等號的方向不變，根據結論可知如果a>b，則a±c> b±c，需驗證a>b時，a+c>b+c.

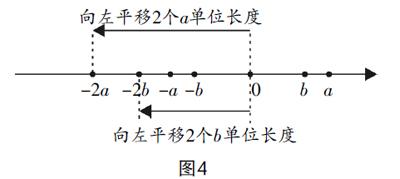
驗證活動：請同學們繪制數軸，在數軸上根據a>b取a和b點的位置，然后將兩點的位置分別向右平移c個單位，如圖3所示.

思考1：結合數軸思考a+c和b+c的大小.

思考2：數軸上點的位置移動后不等符號是否需要改變.

2. 性質3驗證

而對于不等式性質3的數軸驗證，需要利用到數軸上的原點，教學時首先讓學生思考是否需要將零排除在外，然后進行如下引導.

引問1：對于a>b時，若將不等號左右兩邊同乘以-2，則-2a和-2b在數軸上如何取點？

引問2：根據兩點的位置，進一步比較-2a和-2b的大小？

引問3：乘以-2之后，不等式的符號是否發生了改變？

通過上述的數軸驗證，學生可以直觀地認識到同時加上或乘以一個負數后不等式的符號是否發生改變，從而對不等式的性質有了深刻的認識. 這樣做的優勢在于證明過程直觀簡潔，知識關聯性強，通過探究的方式可有效提升學生的能力.

設計環節（四）——語言轉換，素養提升

數學語言是一種較為特殊的語言，不僅可以簡潔地表達數學的性質定理，還具有極強的邏輯性，因此在教學不等式性質時有必要通過文字語言和數學語言的轉換來增強學生對性質的認識，提升學生的語言表達能力.

教學中需要讓學生關注其中的數學符號，以及對應的語言描述，引導學生自主完成語言轉換，建立數學語言與文字語言的對應關系，另外還需思考用數學語言描述性質具有哪些優點.

設計環節（五）——性質應用，解決問題

“性質應用”是性質學習的意義所在，在該階段需要設計多樣的問題，幫助學生鞏固性質，掌握應用性質解決問題的方法. 而在設計問題時除了需要考慮全面性外，還需要考慮所設問題的多樣性，確保代數類問題與實際問題相結合，提升學生思維的寬度和維度.

問題1：用不等式的基本性質，求解下列不等式.

（1）x-5>22;（2）x>50;

（3）3x

問題2：圖5所示是某長方形容器，已知容器長5 cm、寬3 cm、高10 cm，若原容器內有水高3 cm，現先向其中注水，用V表示新注入水的體積，試寫出V的取值范圍.

關于教學設計的反思

1. 整合內容，樹立主線

本節內容是關于不等式的性質教學設計，按照“情景引入—類比探究—語言強化—拓展應用”的主線進行了內容編排. 上述主線的設計是基于對《課程標準》的解讀和教材內容的整合，既關注學生對性質的探究體驗，又注重學生的核心素養提升. 整個教學環節編排合理有序，邏輯嚴密，具有良好的教學效果. 因此，在設計教學時，需要教師深入解讀教材，把握教學重難點，采用合理的方式完成教學引入、環節過渡和能力提升. 同時考慮“知識源于生活，服務于生活”的數學理念，促進學生知識和能力的雙重提升.

2. 類比探究，思維提升

關注學生的知識水平和思維發展是現代教學的基本要求，因此在數學教學設計中需要以學生現有的發展水平為基礎，采用合理的方式結合舊知，幫助學生完成新知的學習. 以本節“不等式的性質”的教學為例，考慮到學生已掌握等式的性質和數軸等知識，在教學時可充分把握知識聯系性，通過類比探究、直觀呈現的方式來引導學生歸納性質，驗證結論. 整個過程以知識探究為主體，以學生的“最近發展區”為基礎，幫助學生完成新知的探究，這樣的教學方式不僅可以讓學生體會到知識間的關聯，還有助于學生思辨思維的發展，為學生核心素養的提升提供高效的平臺.