2018年全國I卷理科解析幾何題的探究與推廣

廣東省佛山市南海區(qū)黃岐高級中學(xué)

熊向前 (郵編：528248)

廣東省廣州市廣東華僑中學(xué)

楊 墁 (郵編：510000)

在看完2018年全國I卷理科數(shù)學(xué)第19題后,現(xiàn)從不同角度對其解法進行了探究,并將其結(jié)論拓展推廣到其他的圓錐曲線中,在追溯其命題背景之后,又發(fā)現(xiàn)了其結(jié)論更為一般的形式.現(xiàn)整理成文,不當(dāng)之處,敬請批評指正.

1 試題呈現(xiàn)

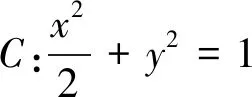
(1)當(dāng)l與x軸垂直時,求直線AM的方程;

(2)設(shè)O為坐標(biāo)原點,證明:∠OMA=∠OMB.(2018年全國I卷理科數(shù)學(xué)第19題)

評注本題考查橢圓的標(biāo)準(zhǔn)方程及其幾何性質(zhì)、直線的方程、直線與橢圓的位置關(guān)系、斜率、韋達定理、等角的證明等基礎(chǔ)知識,考查學(xué)生的推理論證能力、運算求解能力以及綜合運用所學(xué)知識分析問題和解決問題的能力,考查數(shù)形結(jié)合的思想、分類討論的思想、化歸與轉(zhuǎn)化的思想.立意深刻、內(nèi)涵豐富,具有一定的典型性、代表性,極具探究價值,是一道值得研究的好題.

2 解法探究

破解此題的關(guān)鍵:一是畫圖引路,先畫出大致圖形,把題中的數(shù)學(xué)符號語言翻譯成圖形語言;二是合理轉(zhuǎn)化,以數(shù)助形,把幾何關(guān)系等價轉(zhuǎn)換其他的數(shù)量關(guān)系.

證法1當(dāng)設(shè)直線AB與x軸重合時,顯然成立;

當(dāng)設(shè)直線AB與x軸不重合時,由題意F(1,0),設(shè)直線AB的方程為x=my+1,A(x1,y1),B(x2,y2),將x=my+1代入橢圓C的方程，得(m2+2)y2+2my-1=0,則

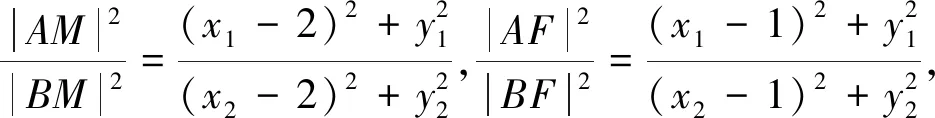
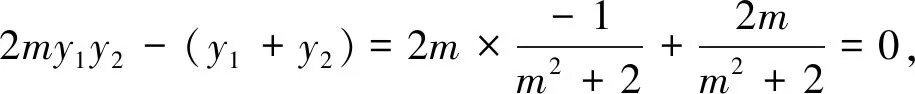
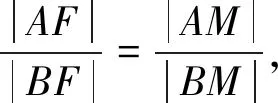
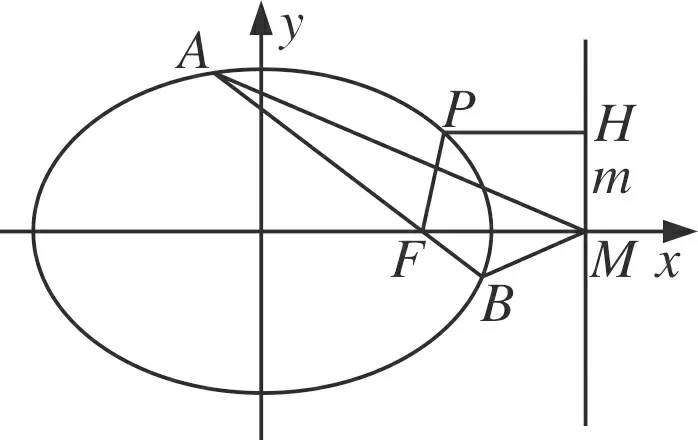
圖1

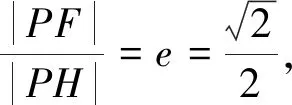
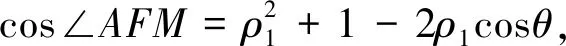
下同證法1.

證法3設(shè)直線l的參數(shù)方程為

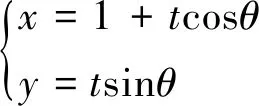
A(1+t1cosθ,t1sinθ),B(1+t2cosθ,t2sinθ),

將(*)代入橢圓C的方程得

(sin2θ+1)t2+2tcosθ-1=0,則

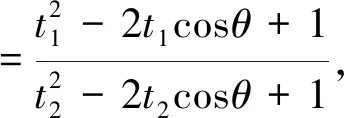
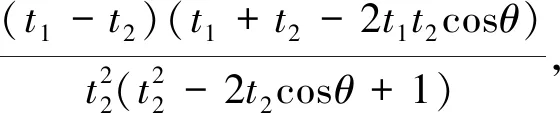
證法4 由證法1知

而2my1y2-(y1+y2)=0,所以kAM+kBM=0,從而得直線AM與直線BM的傾斜角互補,所以∠AMO=∠BMO.

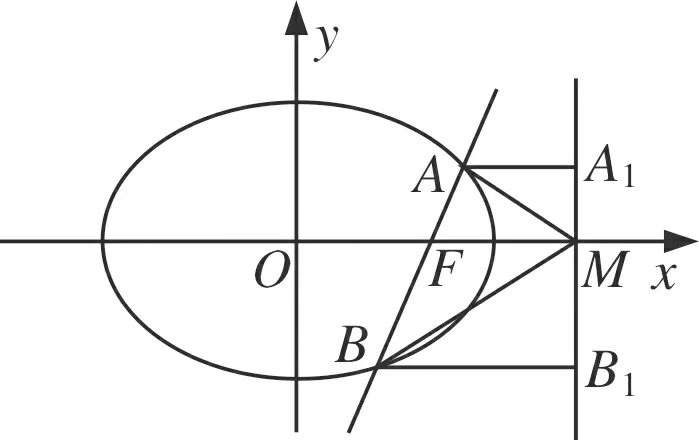
圖2

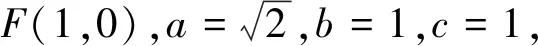
評注在以上方法中,前三種方法均借助于三角形內(nèi)角平分線定理,把要證明的角的關(guān)系轉(zhuǎn)化成線段間的數(shù)量關(guān)系,方法1是運用兩點間的距離公式,思路簡單直接,但計算量大;方法2是把圖形放在極坐標(biāo)系下,運用極坐標(biāo)系中方程的特點,減小了計算量,但對極坐標(biāo)系的知識要求高;方法3是運用直線的參數(shù)方程,亦將計算量減小.方法4借助于斜率與傾斜角的關(guān)系,大大減小了運算,體現(xiàn)了解析幾何中數(shù)形結(jié)合的思想.方法5從圖形的幾何性質(zhì)出發(fā),運用相似三角形的性質(zhì),屬于純幾何證法,讓我們看到了問題的本質(zhì).

3 拓展推廣

3.1 在橢圓中的一般化推廣

從上面證法5可知,對于一般的橢圓,只要M點為橢圓的右準(zhǔn)線與x軸的交點,那么上述性質(zhì)一定成立,即:

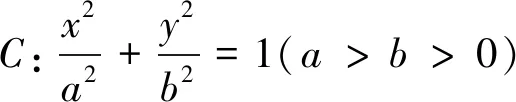
在上述定理中,我們發(fā)現(xiàn)焦點F與定點M的橫坐標(biāo)之間存在一定的聯(lián)系,即乘積等于定值a2,那么,若將F點換成一般的點P(m,0),保證P、M兩點的橫坐標(biāo)的乘積為定值a2,是否又有類似的性質(zhì)呢？筆者借助GeoGebra軟件進行探究,得出如下結(jié)論:

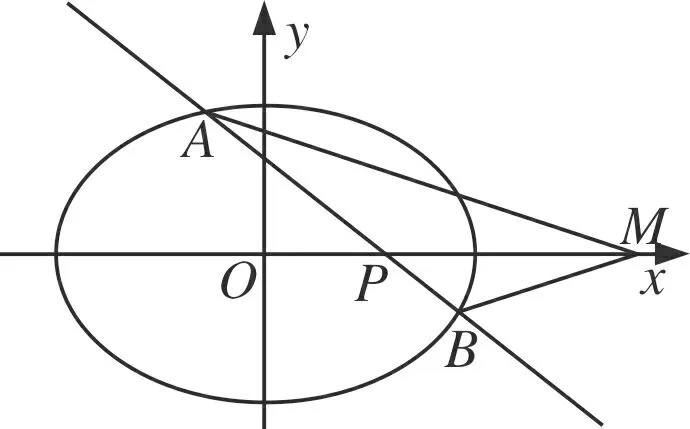
圖3

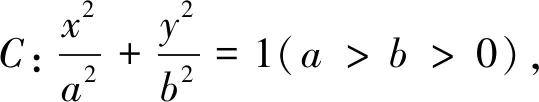
證明當(dāng)設(shè)直線AB與x軸重合時,顯然成立;當(dāng)設(shè)直線AB與x軸不重合時,設(shè)直線AB的方程為x=ty+m,A(x1,y1)、B(x2,y2),將x=ty+m代入橢圓C的方程，得(t2b2+a2)y2+2tmb2y+(m2-a2)b2=0,則

=0,

從而得直線AM與直線BM的傾斜角互補,所以∠AMP=∠BMP.

圖4

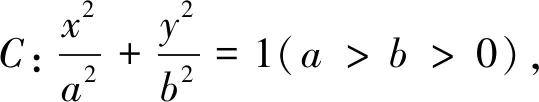
在定理3中,將直線l繞著P點旋轉(zhuǎn),當(dāng)A、B兩點無限靠近時,∠AMP與∠BMP的大小無限接近,當(dāng)A、B重合時, ∠AMP=∠BMP=900,此時AM⊥x軸,直線l與橢圓C只有一個交點,直線l與橢圓C相切,于是我們進一步得出結(jié)論:

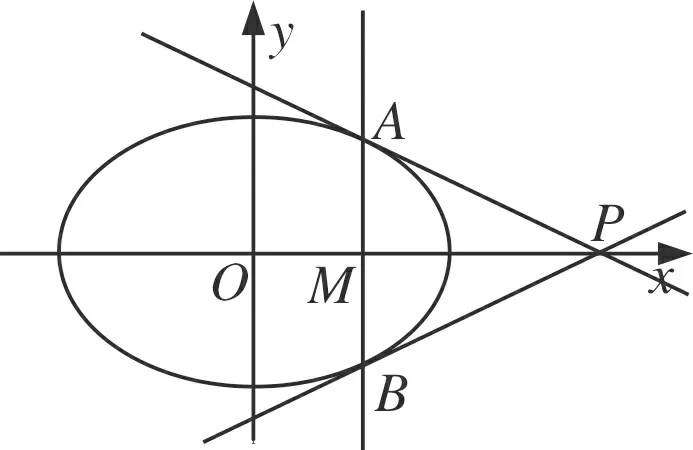
圖5

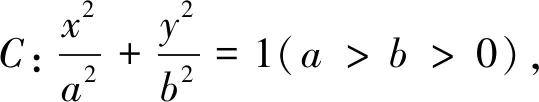
3.2 在雙曲線、拋物線中的推廣

類比橢圓,在雙曲線、拋物線中是否有類似的結(jié)論呢？筆者又借助于GeoGebra軟件進行了探究,得出以下結(jié)論:

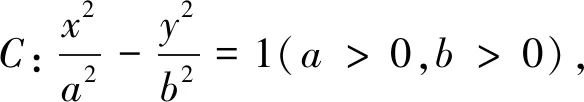
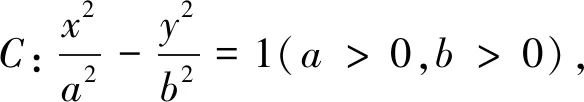
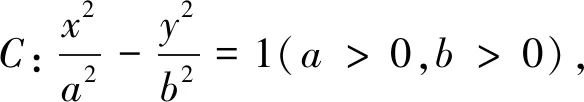
定理6已知拋物線C:y2=2px,點P(m,0)(m>0)是拋物線C內(nèi)一點,過點P作直線l與拋物線C交于A、B兩點,M(-m,0),則∠AMP=∠BMP.

定理7已知拋物線C:y2=2px,點P(m,0)(m<0)是拋物線C外一點,過點P作直線l與拋物線C交于A、B兩點,M(-m,0),則∠AMP=1800-∠BMP.

推論3已知拋物線C:y2=2px,點P(m,0)(m<0)是拋物線C外一點,過點M(-m,0)與x軸垂直的直線l與拋物線C于A、B兩點,則直線PA、PB與拋物線C相切.

4 背景探源

在以上關(guān)于橢圓、雙曲線的結(jié)論中,都有M、P兩點的橫坐標(biāo)之積為定值a2;而在拋物線中,都有M、P兩點的橫坐標(biāo)互為相反數(shù),這是偶然還是必然呢？經(jīng)過研究發(fā)現(xiàn),這與圓錐曲線的極點、極線的知識有關(guān).實際上,在近年來全國各地的高考卷中,有著極點與極線知識背景的試題經(jīng)常出現(xiàn),我們雖不能直接利用極點與極線的相關(guān)結(jié)論進行解答,但教師如果掌握了其中的相關(guān)理論,就能從更高的角度看問題,把問題看得更透徹,這對我們教學(xué)是有很大幫助的.

借用文[1]給出圓錐曲線中極點與極線的定義:

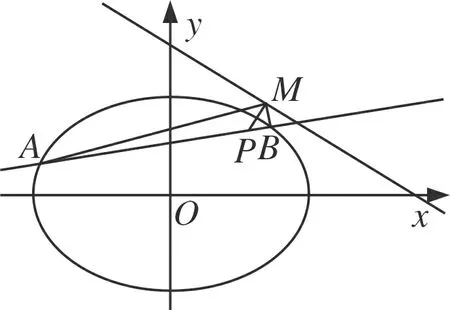
圖6

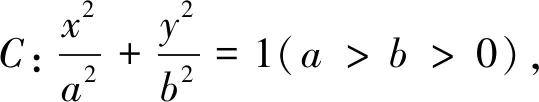
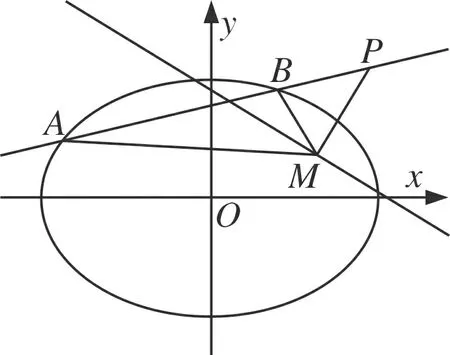
圖7

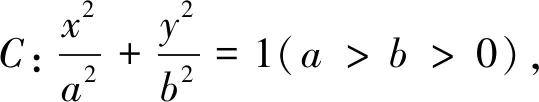
對于以上兩個結(jié)論,可利用GeoGebra軟件驗證成立,限于篇幅,在此不再證明,感興趣的讀者可自行證明.

5 高考鏈接

理解以上結(jié)論,對解答一些高考試題有一定的幫助,下面列舉數(shù)例加以說明.

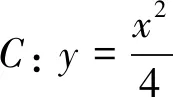
(2)(2015年福建文科數(shù)學(xué)第19題)已知點F為拋物線E;y2=2px(p>0)的焦點,點A(2,m)在拋物線E上,且|AF|=3,(Ⅰ)求拋物線E的方程;(Ⅱ)已知點G(-1,0),延長AF交拋物線E于點B,證明：以點F為圓心且與直線GA相切的圓,必與直線GB相切.

(3)(2013年陜西卷理科數(shù)學(xué)第20題)已知動圓過定點A(4,0), 且在y軸上截得的弦MN的長為8. (Ⅰ)求動圓圓心的軌跡C的方程; (Ⅱ)已知點B(-1,0), 設(shè)不垂直于x軸的直線l與軌跡C交于不同的兩點P、Q, 若x軸是∠PBQ的角平分線, 證明直線l過定點.

以上幾例問題的第二問及2018年全國卷解析幾何題雖然考查的載體和設(shè)問方式各異,但本質(zhì)上都是在考過定點的動直線與圓錐曲線所形成的等角問題.2018年全國卷考的是已知定點與動直線證明等角.2015年全國卷考的是已知等角探究定點的存在性.2015年福建卷是綜合拋物線與圓間接性考等角的證明.2013年陜西卷考的是已知等角證明動直線過定點.無論如何變化,其考查的本質(zhì)不變,解答的方法也幾乎一樣.因此,在高三復(fù)習(xí)備考中我們要重視高考真題的訓(xùn)練,在課堂上要精選典型真題進行講解,幫助學(xué)生把握其實質(zhì),掌握其規(guī)律,讓學(xué)生在訓(xùn)練的過程中發(fā)散思維、提高能力.

通過本文的探究,我們進一步認(rèn)識到各圓錐曲線之間規(guī)律的統(tǒng)一性,當(dāng)我們在一個曲線中得到一個規(guī)律時,往往可以將之進行推廣,得出更普遍、更一般的規(guī)律.正如波利亞所說的“解題就像采蘑菇一樣,當(dāng)我們發(fā)現(xiàn)一個蘑菇時,它的周圍可能有一個蘑菇圈. ”