字母代數巧解題

筅山東省濟南市萊蕪區雪野鎮中心中學 陳 燁

在復習整式乘法公式的課堂上，老師讓一名學生證明這樣一個命題：任意兩個連續奇數之平方差必然是8的整數倍.那名學生是這樣證明的：假設這兩個連續奇數分別為1、3，那么32-12=8，是8的整數倍；假設這兩個連續奇數分別為17、19，那么192-172=（19+17）（19-17）=16×2=32=8×4，也是8的整數倍……假設這兩個連續奇數分別為99、101，那么1012-992=（101+99）（101-99）=200×2=400=8×50，仍然是8的整數倍.所以任意兩個連續奇數之平方差必然是8的整數倍.這名學生的證法是否正確？答案是否定的.原因在于，這個學生只是通過舉例的方法，驗證了一些連續奇數符合“平方差是8的整數倍”，但這些數并不能代表所有的連續奇數，因此證明錯誤.那么這道題應該如何證明呢？首先，應該正確表示出兩個連續奇數.設n表示任意整數，那么兩個連續奇數可以分別用2n-1、2n+1表示，則（2n+1）2-（2n-1）2=［（2n+1）+（2n-1）］·［（2n+1）-（2n-1）］=4n×2=8n，顯然是8的整數倍.這種證法由于我們分別用2n-1、2n+1表示全體連續奇數，因而正確.在證明過程中，我們用n表示任意整數，進而順利地表示出任意奇數2n-1，任意連續奇數2n-1、2n+1，從而順利完成證明.這里滲透了一種字母代數思想.用字母代替或表示數是數學的一大進步，這樣可以使字母也參與到數學運算中來.運用字母代數思想，可以使復雜的數學問題變得簡單，常能起到以簡馭繁、化難為易之效.下面以例子分類說明字母代數思想在解決初中數學問題中的應用，希望對讀者有所幫助.

一、運用字母代數進行計算或比較大小

例 1計 算?-3636×3638.

分析：本題若直接計算，由于所給數據較大，因而比較煩瑣.注意到所給數據比較接近，因而可設3637=a.

解：設3637=a，則原式=-（a-1）（a+1）

=a2-10-（a2-1）

=-9.

分析：本題若按常規方法，需要先計算括號內的.由于括號內分數較多，因而這種方法并不現實.注意到括號內含有一些相同的項，可用字母來表示這些相同的項，再計算就方便多了.

解：令=n，則原式=（1+m）n-（1+n）m=n-m=

點評：通過以上兩例不難看出，運用字母代數在解決一些計算問題時，不僅可以使原式的書寫簡單，而且可以使一些項相互抵消，順利求出原式的值.

牛刀小試：若x=123456789×123456786，y=123456788×123456787，則x、y的大小關系是（ ）.

A.x=y B.x＜y C.x＞y D.不確定

二、運用字母代數求代數式的值

分析：本題若采用直接代入的方法求解不勝其煩.觀察待求式中的常數與條件式中的常數，我們發現都有這個常數.于是我們想到先由a=-1表示出=a+1，然后代入原式求值.

原式=a5+2a4-（a+1）2a3-a2+［（a+1）2+1］a-（a+1）2

=a5+2a4-（a2+2a+1）a3-a2+（a2+2a+1+1）a-（a2+2a+1）

=a5+2a4-a5-2a4-a3-a2+a3+2a2+2a-a2-2a-1=-1.

點評：本題表面上看是一個已知字母的值求代數式的值問題，通過字母代數，將本題變成一個簡單的整式運算問題.

例4已知6（a-b）+（b-c）+（c-a）=0（a≠b），求的值.

解：已知條件可以為形為（）（2a-b）+（b-c）+（c-a）=0.又（a-b）·12+（b-c）·1+（c-a）=0，逆用一元二次方程的根與系數關系定理，知、1是關于x的一元二次方程（a-b）x2+（b-c）x+（c-a）=0（a≠b）的兩根.

三、運用字母代數因式分解

例5 在實數范圍內分解因式x3-2x+（1-）x2+7.

分析：解答本題的常規方法是將x看成字母分組分解，但比較困難.通過仔細觀察原式中的常數，必然會引起注意.如果將看成字母，將原式整理成關于的二次三項式，再分解就簡單多了.

牛刀小試：在實數范圍內分解因式x3-2x+（1-

四、用字母代數進行證明

例6證明：兩個連續偶數的平方和與4的差一定能被16整除.

證明：設n為整數，則兩個連續偶數可以分別用2n和2n+2表示.這兩個連續偶數的平方和與4的差為（2n+2）2+（2n）2-4=4n2+8n+4+4n2-4=8n2+8n=8n（n+1）.注意到n、n+1是兩個連續整數，這兩個連續整數中必然有一個是偶數，因此8n（n+1）必然是16的整數倍，即兩個連續偶數的平方和與4的差一定能被16整除.

例7證明：十位數字相同而個位數字之和等于10的兩個兩位數的乘積與該兩位數的個位數字乘積之差能被200整除.

證明：設一個兩位數的十位數字為m，個位數字為n，另一個兩位數的十位數字也為m，個位數字為10-n，則這兩個兩位數的乘積與該兩位數的個位數字乘積之差為 （10m+n）（10m+10-n）-n （10-n）=100m2+100m-10mn+10mn+10n-n2-10n+n2=100m2+100m=100m（m+1）.注意到m、m+1是兩個連續整數，這兩個連續整數中必然有一個是偶數，因此100m（m+1）必然是200的整數倍，即100m（m+1）能被200整除.

牛刀小試1：證明：如兩個整數之差為6，那么這兩個整數的平方差一定是12的整數倍.

牛刀小試2：證明：如果一對兩位數的個位數字之積等于十位數字之積，將每個兩位數的個位數字與十位數字對調，那么對調后的兩位數之積等于原兩位數之積.

五、用字母代數求陰影部分的面積

例7如圖1，矩形ABCD中，AB=2cm，BC=6cm，點E為AB邊上任意一點，四邊形BEMN也是矩形，且BN=3BE，則陰影部分的面積等于＿＿＿＿＿＿cm2.

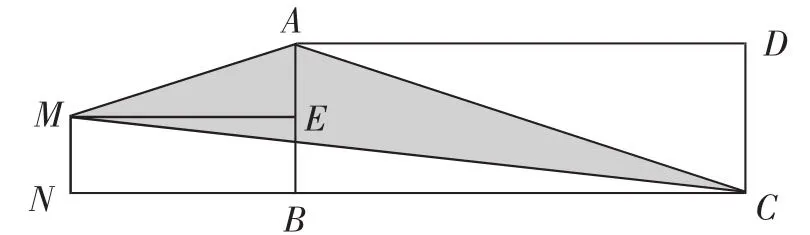
圖1

解：設BE=a cm，則BN=3a cm.S陰影=S梯形ABMN+S△ABCS△MNC=（a+2）×3a+×2×6-a（3a+6）=a2+3a+6-a2-3a=6（cm2）.

說明：可以看出，陰影部分的面積與BE的長短無關，僅與矩形ABCD的面積有關，且S陰影=S矩形ABCD.另外，本題亦可連接BM，然后證明△MNB △ABC，這樣才可得出BM∥AC，進而利用同底等高的三角形面積相等解答.

牛刀小試：如圖2，四邊形ABCD和ECGF都是菱形，且四邊形ABCD的邊長為2，∠A=120°，則圖中陰影部分的面積是（ ）.

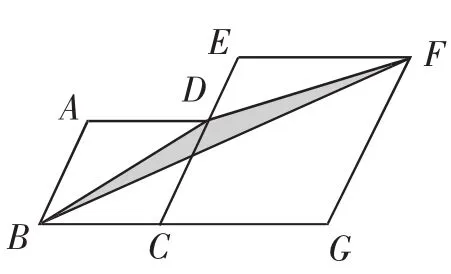
圖2

以上談論了字母代數在解決初中數學問題中的應用.可以看出，有些數學問題必須用字母代數才能解決.另一方面，應用字母代數思想確實可以使某些數學問題獲得簡解.希望大家能夠掌握字母代數思想，并力求應用這種數學思想解決問題.