“三步+圖象”解決傳送帶運動問題
河北
傳送帶在日常生產和生活中有著廣泛的應用,在車站、機場、工廠等隨處可見,有關傳送帶問題的考題更是頻繁出現在高中生的各類考卷中,考查學生的科學素養和實踐應用能力。有關傳送帶問題也一直是高中物理學習中的一個難點問題,很多同學在解決有關傳送帶問題時比較“犯怵”,其難點在于物體與傳送帶間運動的牽制,會產生摩擦力的突變,比如靜摩擦力消失,滑動摩擦力突然變為靜摩擦力,靜摩擦力突然變為滑動摩擦力,滑動摩擦力的方向突然改變等等,致使學生在解決問題中出現錯誤。其實,無論多么復雜的傳送帶問題,如果分析清楚以下三個問題,以圖象輔助分析,都能輕松地得以解決。
第一步:“受力分析求加速度”,即根據物體與傳送帶的運動情況進行受力分析,求物體的加速度;
第二步:“何時、到哪兒兩等速”,即分析多長時間,物體走了多少位移與傳送帶速度相等;
第三步:“等速后能否共速”,即根據具體條件分析,物體與傳送帶速度相等后能不能以相同的速度一起運動,當物體與傳送帶速度相等時往往會發生摩擦力種類、大小及方向的突變。
如果按以上思路分析并回答了上述問題,再結合牛頓運動定律及運動學公式、動能定理等物理規律,以運動圖象為輔助分析運動過程,傳送帶問題便不是什么難題,下面以常見的問題類型分別舉例分析。
一、水平傳送帶上的力與運動情況分析
【例1】水平傳送帶被廣泛地應用于車站、碼頭、工廠、車間。如圖1所示為水平傳送帶裝置示意圖,繃緊的傳送帶AB始終保持v0=2 m/s的恒定速率運行,一質量為m的工件無初速度地放在A處,傳送帶對工件的滑動摩擦力使工件開始做勻加速直線運動,設工件與傳送帶間的動摩擦因數為μ=0.2,AB之間的距離為L=10 m,g取10 m/s2。求工件從A處運動到B處所用的時間。

圖1
【解析】(第一步,先對工件進行受力分析,求加速度)
工件剛放到傳送帶上時μmg=ma
代入數據可得a=2 m/s2
(第二步,計算速度相等時所用時間和位移)
設加速過程對應的時間為t1,位移為l
代入數據可得t1=1 s
代入數據可得l=1 m
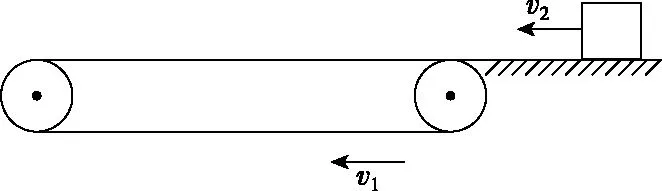
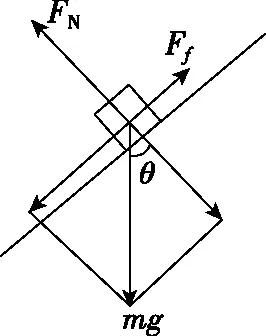
由于l (第三步,分析等速后能否與傳送帶一起運動,本問題中工件與傳送帶速度相等后摩擦力消失) 設工件隨傳送帶勻速運動的時間為t2,則 所以工件從A處運動到B處的總時間 t=t1+t2=5.5 s 【反思歸納】這是一道傳送帶以恒定速度運轉,而被運送的工件初速度為0的實際問題,解決這類問題首先要對被運送的工件進行受力分析,一般情況下,工件在傳送帶上有兩種運動形式,一是勻加速運動,二是勻速運動。從勻加速運動到勻速運動過程中,往往要對工件在傳送帶上做加速運動結束時是否滑離傳送帶做出判斷,如果已經滑離傳送帶,則工件不存在勻速運動階段,如果沒有滑離,則工件將與傳送帶一起做勻速運動,可見工件是否滑離傳送帶的判斷是不能忽視的。 【例2】如圖2所示為車站使用的水平傳送帶模型,傳送帶長L=8 m,以速度v=2 m/s沿順時針方向勻速轉動,有一旅客將一個質量為m=4 kg的行李箱以v0=8 m/s的初速度水平滑上傳送帶。已知行李箱與皮帶間的動摩擦因數為μ=0.5,則行李箱從傳送帶的A端到B端所需要的時間是多少,在滑動過程中摩擦產生的熱量為多少?(g=10 m/s2,且可將行李箱視為質點。) 圖2 圖3 【解析】(第一步,對行李箱進行受力分析,求加速度。行李箱受力情況如圖3所示,行李箱受到自身重力mg,傳送帶給予的支持力FN,傳送帶對行李箱的滑動摩擦力Ff方向水平向左) 由牛頓第二定律得μmg=ma 解得a=5 m/s2,方向向左,做減速運動 (第二步,計算行李箱與傳送帶速度相等時所用時間和位移) 設行李箱在傳送帶上做勻減速運動的時間為t1,則 代入數據得t1=1.2 s 此時行李箱通過的位移為x1,由勻減速運動的規律得 解得x1=6 m 可知在勻減速運動階段,行李箱沒有滑離傳送帶。 (第三步,分析等速后能否與傳送帶一起運動,本問題中行李箱與傳送帶速度相等后摩擦力消失) 代入數據可得t2=1 s 故行李箱在傳送帶上運動的時間為t=t1+t2=2.2 s 兩個物體因摩擦產生的熱量等于兩者間的摩擦力與相對路程的乘積 相對路程Δs=x1-vt1 產熱為Q=μmg·Δs 代入數據得Q=72 J 【反思歸納】例2與例1最大的區別是被運送物體的初速度比傳送帶運動的速度要大得多,這一題設條件的變化,直接影響到工件在傳送帶上所受滑動摩擦力的方向,此時摩擦力所起到的作用不是使例1中物體加速,而是使物體減速。顯而易見初始運動情況會影響受力情況,進而影響后來的運動情況,注意計算產生熱量為摩擦力與相對路程的乘積。 【例3】如圖4所示,一足夠長的水平傳送帶以恒定的速度v1沿順時針方向轉動,傳送帶右端有一與傳送帶等高的光滑平臺,一小物塊以恒定速度v2沿直線向左滑上傳送帶后,經過一段時間又返回光滑平臺,返回時物塊的速率為v2′,則下列關于返回物塊速率的說法正確的是 ( ) 圖4 A.只有v1=v2時,才有v2′=v1 B.若v1>v2時,則v2′=v2 C.若v1 D.不管v2多大,v2′=v2 【解析】第一步,對物體進行受力分析,求加速度。本題中物體速度與傳送帶速度方向相反,受到摩擦力向右,可知物體先向左減速運動,減速到0后向右做勻加速直線運動,整個過程中,加速度不變。 第二步,計算物體與傳送帶速度相等時所用時間和位移。本題中沒有確定給出物塊與傳送帶間的動摩擦因數以及兩者的速度關系,用圖象法進行半定量分析會使問題變得更為簡單,如圖5所示,設速度方向向左為正方向,圖象中速度與時間軸所夾的面積上下兩部分相等時返回出發點。 圖5 第三步,分析等速后能否與傳送帶一起運動,本問題中小物塊與傳送帶速度相等后摩擦力消失,由圖象可以看出,當v1>v2時,還沒有達到與傳送帶速度相等就已經返回了,而當v1 綜上分析,本題答案為B。 【反思歸納】按以上三步分析清楚物理過程,在此基礎上,結合圖象便可很容易得出正確答案。本題以“力和運動的關系”知識為載體,著眼于考查學生的理解能力、推理能力、綜合分析能力、建立理想模型來解決實際問題的能力,能很好地考查考生的物理核心素養。 【例4】如圖6所示,一傳送帶傾斜放置與水平方向夾37°角,兩端點AB距離為L=16 m,傳送帶以恒定速度v=10 m/s運動,在傳送帶上端A處無初速釋放質量為m=0.5 kg的物塊,物塊與帶面間的動摩擦因數μ=0.5,求: 圖6 (1)當傳送帶順時針轉動時,物塊從A到B所經歷的時間為多少? (2)當傳送帶逆時針轉動時,物塊從A到B所經歷的時間為多少?(sin37°=0.6,cos37°=0.8,取g=10 m/s2) 【解析】(1)(第一步,對物塊進行受力分析,求加速度。當傳送帶順時針轉動時,傳送帶相對物塊向上運動,所以傳送帶受到物塊的摩擦力沿傳送帶向下,物塊受傳送帶的摩擦力方向向上,如圖7所示,由于mgsin37°>μmgcos37°,故物塊向下作初速度為0的勻加速運動直到B處。不存在分析第二、三步) 圖7 根據牛頓第二定律得 mgsin37°-μmgcos37°=ma 代入數據可得a=2 m/s2 物塊在傳送帶上做加速度為a=2 m/s2的勻加速運動,設運動時間為t,則 代入數據可得t=4 s (2)(第一步,對物塊進行受力分析,求加速度) 物塊放上傳送帶的開始的一段時間受力情況如圖8所示,剛放物塊時受摩擦力方向沿斜面向下,設加速度為a1,由牛頓第二定律得 圖8 mgsin37°+μmgcos37°=ma1 解得a1=10 m/s2,作初速為0的勻加速運動。 (第二步,計算物塊與傳送帶速度相等時所用時間和位移) 設物塊加速時間為t1,則 解得t1=1 s (第三步,分析等速后能否與傳送帶一起運動) 速度相等后物塊便與傳送帶產生向下運動趨勢,比較mgsin37°與μmgcos37°發現物體不能與傳送帶相對靜止,將沿傳送帶加速下滑。 設速度相等后物塊的加速度為a2,其受力情況如圖9所示。由牛頓第二定律可知 圖9 mgsin37°-μmgcos37°=ma2 解得a2=2 m/s2 設后一階段物塊下滑到底端所用的時間為t2可得 解得t2=1 s 所以物塊從A到B的時間為 t=t1+t2=2 s 【反思歸納】解答本題的關鍵是分析摩擦力的方向,以及摩擦力向上和向下的條件。審題時應注意對已知條件作必要的定性分析和半定量的分析。如由本題中給出的μ和θ值可作出以下判斷:當μ≥tanθ時,物塊在加速至與傳送帶速度相同后,物塊將與傳送帶相對靜止,并同傳送帶一起勻速運動;當μ 【例5】倉庫中常用的皮帶傳輸裝置示意圖如圖10所示,它由兩臺皮帶傳送機組成,一臺水平傳送,A、B兩端相距3 m,另一臺傾斜,傳送帶與地面的傾角為θ=37°,C、D兩端相距4.45 m,B、C相距很近。水平傳送以5 m/s的速度沿順時針方向轉動,現將質量為10 kg的一袋大米無初速度地放在A端,它隨傳送帶到達B端后,速度大小不變地傳到傾斜送帶的C點,米袋與兩傳送帶間的動摩擦因數均為0.5。(本題中g取10 m/s2,sin37°=0.6,cos37°=0.8) 圖10 (1)若CD部分傳送帶不運轉,求米袋沿傳送帶在CD上所能上升的最大距離; (2)若傾斜部分CD以4 m/s的速率順時針方向轉動,求米袋從C運動到D所用的時間。 【解析】(1)(第一步,對物塊進行受力分析,求加速度) (第二步,計算米袋與傳送帶速度相等時所用時間和位移) (第三步,分析等速后能否與傳送帶一起運動) 米袋加速一段后與傳送帶一起勻速運動到達B點,到達C點時速度v0=5 m/s 到達CD段后,設米袋在CD上運動的加速度大小為a 由牛頓第二定律得mgsinθ+μmgcosθ=ma 代入數據得a=10 m/s2 (2)傾斜部分傳送帶沿順時針方向轉動時,繼續考慮分析相關的三個問題來解決問題。 (第一步,對物塊進行受力分析,求加速度) 米袋速度減為4 m/s之前的加速度為 a1=-g(sinθ+μcosθ)=-10 m/s2 (第二步,計算米袋與傳送帶速度相等時所用時間和位移,本題中只考慮位移) (第三步,分析等速后能否與傳送帶一起運動) 米袋速度等于4 m/s時,滑動摩擦力方向改變,由于μmgcosa a2=-g(sinθ-μcosθ)=-2 m/s2 可見,米袋速度減速到0時,恰好運行到D點 米袋從C運動到D所用的時間t=t1+t2=2.1 s。 【反思歸納】解答此題的關鍵是準確分析物塊在水平和傾斜傳送帶上的受力情況,并據此分析出物塊在兩種狀態的傳送帶上的運動情況。在具體的分析過程中應該注意物塊在水平和傾斜傳送帶上受力和運動情況的特點來分析,可以很好的考查學生對力和運動的物理觀念。

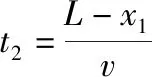

二、傾斜傳送帶上的力與運動情況分析




三、水平和傾斜組合傳送帶上的力與運動情況分析







