例談解析幾何主元選取和背景挖掘

魏建華

[摘? 要] 在2018年的全國卷理科解析幾何大題的講解中，逐層地選取不同的主元進行求解，同時對問題追根溯源，并簡單運用共軛極點理論解決這類型問題.

[關鍵詞] 解析幾何;主元選取;背景挖掘;共軛極點

解析幾何問題的求解方法綜合，思維發散，聯系和應用不同板塊的知識可得到不同的邏輯線索，從而選定不同主元（主要變量，其他變量為中間變量）進行求解. 經典解析幾何問題，往往蘊含著深刻的背景，我們需要對其進行深度剖析，以對圓錐曲線性質有更深刻的認識. 下面就全國Ⅰ卷理科第19題聯系不同板塊知識給出四種主元選取角度及對命題背景做深度挖掘和簡單運用.

作圖1，本題就兩個主要幾何關系，A，B在過點F的直線上和在橢圓上. 一個是線性關系，一個是非線性關系. 因為直線l與x軸重合或垂直時，結論顯然，下面不再贅述. 當直線l與x軸不重合或垂直時，自然從線性關系入手，聯系直線方程相關知識. 因為知道直線的橫截距，所以將直線的斜率作為主元.

方法1：選定直線斜率的倒數作為主元

當直線AB與x軸不重合時，我們設直線AB的方程為x=my+1.

評析：此解法很自然，將本問題與解三角形有機結合，運用知識，體現能力，也鍛煉學生的轉化思想和能力.當然我們也可以先從非線性關系入手，利用點在橢圓上這個關系，自然想到橢圓的參數方程，此時我們將離心角作為主元進行求解.

評析：本方法很自然但是運算難度大，要求對三角形和差公式有深度了解且能靈活運用，培養思維，鍛煉能力.我們能不能直接從目標入手對結論再次進行等價轉化呢？顯然，還可轉化成射線MA，MB的傾斜角之間的關系，只需證明其傾斜角之和為2π即可. 所以我們以點M為極點，x軸正方向為極軸建立極坐標系，利用極坐標進行求解，但是這種方法運算過于復雜，故而略去.

小結：四種做法聯系不同板塊知識，產生不同的解題線索，因而得到不同的主元選取角度，關鍵是點在直線上和點在橢圓上這兩個幾何條件應用順序不同所致，但四種做法有機組成幾何代數兩種處理問題的模式.不同主元的選取由淺入深，既伴隨著學生運算素養的提升，又伴隨著轉化意識的加強.

追根溯源

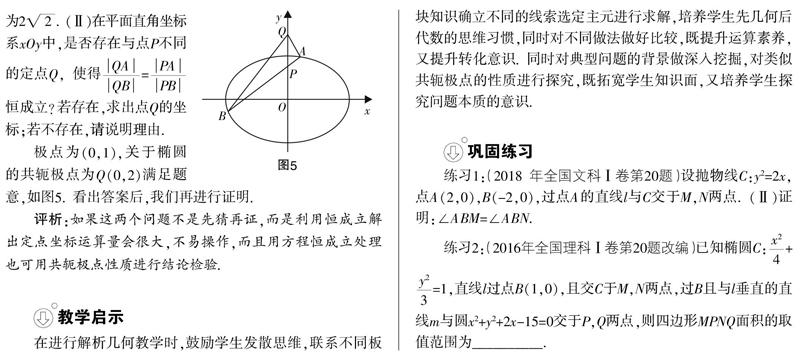
我們把這個結果當成橢圓的性質來思考，很明顯大家觀察到點F是橢圓焦點，點M是右準線與坐標軸的交點，我們做出猜想：這個性質是否對圓錐曲線都成立. 同時我們看到2018年全國Ⅰ卷文科高考題第20題就是把圓錐曲線換成了拋物線去證明這個結論. 我們再深層次地挖掘可聯想到《高等幾何》里的極點極線理論.

評析：如果這兩個問題不是先猜再證，而是利用恒成立解出定點坐標運算量會很大，不易操作，而且用方程恒成立處理也可用共軛極點性質進行結論檢驗.

教學啟示

在進行解析幾何教學時，鼓勵學生發散思維，聯系不同板塊知識確立不同的線索選定主元進行求解，培養學生先幾何后代數的思維習慣，同時對不同做法做好比較，既提升運算素養，又提升轉化意識. 同時對典型問題的背景做深入挖掘，對類似共軛極點的性質進行探究，既拓寬學生知識面，又培養學生探究問題本質的意識.