基于高中數(shù)學(xué)核心素養(yǎng)的課堂數(shù)學(xué)意識的構(gòu)建策略

江西省廣昌縣第一中學(xué) 劉經(jīng)標(biāo)

隨著新一輪基礎(chǔ)教育課程改革的實(shí)施與推進(jìn)，數(shù)學(xué)核心素養(yǎng)的提出，對高中數(shù)學(xué)教學(xué)以及對高中生的培養(yǎng)提出了新的要求。高中數(shù)學(xué)教師在開展教學(xué)的過程中，應(yīng)該具有創(chuàng)造性地充分利用教材，并通過行之有效的策略，對數(shù)學(xué)教材中的內(nèi)容進(jìn)行加工，以此實(shí)現(xiàn)課堂數(shù)學(xué)意識的構(gòu)建，從而促進(jìn)高中生數(shù)學(xué)核心素養(yǎng)的提高，扎實(shí)地掌握數(shù)學(xué)的觀點(diǎn)與方法，培養(yǎng)高中生發(fā)現(xiàn)問題、分析問題以及解決問題的數(shù)學(xué)能力。

一、核心素養(yǎng)下對高中生培養(yǎng)的基本要求

1.自主性基本要求

新一輪基礎(chǔ)教育課程改革中所提倡的體現(xiàn)高中生在教學(xué)中的主體位置與核心素養(yǎng)下自主性的培養(yǎng)要求相符合。核心素養(yǎng)下對高中生自主性培養(yǎng)，要求高中生能夠在學(xué)習(xí)數(shù)學(xué)知識的過程中，自主地制訂學(xué)習(xí)計(jì)劃、安排學(xué)習(xí)進(jìn)度并自主地進(jìn)行自我管理。而這種自主能力正是現(xiàn)代社會(huì)對人才所要求的，同時(shí)也是現(xiàn)階段高中生所缺乏的，因此，高中數(shù)學(xué)核心素養(yǎng)下，應(yīng)該加強(qiáng)對高中生自主能力的培養(yǎng)。

2.探究性的基本要求

高中數(shù)學(xué)是一門具有較強(qiáng)邏輯性的學(xué)科，并且知識內(nèi)容和概念較為繁雜，這就對高中生的邏輯思維能力和探究能力提出了更高的要求。因此，在基于高中數(shù)學(xué)核心素養(yǎng)的課堂教學(xué)中應(yīng)該注重培養(yǎng)高中生的探究能力和邏輯思維能力，以此提高高中生的數(shù)學(xué)學(xué)習(xí)效果。這一點(diǎn)對課堂數(shù)學(xué)意識的構(gòu)建以及數(shù)學(xué)知識的延伸均具有重要的意義。

3.創(chuàng)新性的基本要求

對于現(xiàn)階段的社會(huì)來說，創(chuàng)新性是現(xiàn)代社會(huì)對人才的一項(xiàng)基本要求，同時(shí)創(chuàng)新也是促進(jìn)社會(huì)發(fā)展的源動(dòng)力。但目前，學(xué)生創(chuàng)新能力還需要進(jìn)一步提升，教學(xué)活動(dòng)開展層面進(jìn)行對應(yīng)調(diào)整與優(yōu)化的緊迫感也十分明顯，如何更好地在教學(xué)中進(jìn)行轉(zhuǎn)變，對學(xué)生創(chuàng)新能力進(jìn)行培養(yǎng)也是值得思考的現(xiàn)實(shí)問題。也就是說，在核心素養(yǎng)下的高中數(shù)學(xué)教學(xué)中，教師應(yīng)該加強(qiáng)對高中生創(chuàng)新性能力的培養(yǎng)，以此促使高中生能夠更好地適應(yīng)于社會(huì)的發(fā)展需求。

二、基于高中數(shù)學(xué)核心素養(yǎng)的課堂教學(xué)意識的構(gòu)建策略

1.通過問題情境，培養(yǎng)高中生的數(shù)學(xué)意識

現(xiàn)階段，問題情境教學(xué)方法是基于高中數(shù)學(xué)核心素養(yǎng)下課堂教學(xué)中較為經(jīng)常性運(yùn)用的一種教學(xué)方法，并且取得了一定的教學(xué)成果。但是隨著教育事業(yè)的不斷發(fā)展，目前問題情境教學(xué)方法也面臨著新的問題，這就需要采取一定的措施進(jìn)行彌補(bǔ)和突破。問題情境教學(xué)方法在基于高中數(shù)學(xué)核心素養(yǎng)的數(shù)學(xué)教學(xué)中的運(yùn)用，問題情境的創(chuàng)設(shè)是否只能夠來源于實(shí)際生活？是通過數(shù)學(xué)知識去解釋實(shí)際生活，還是通過實(shí)際生活詮釋數(shù)學(xué)知識？在教學(xué)中，經(jīng)常是將數(shù)學(xué)教學(xué)內(nèi)容生活化，而并非是將實(shí)際生活中的問題數(shù)學(xué)化。對于高中數(shù)學(xué)知識來說，其源于生活，但又高于生活。

例如，在《曲線與方程》的創(chuàng)設(shè)情境與設(shè)問舉例中，四葉草是三葉草的稀有變種。據(jù)說大約一萬至十萬株三葉草中才會(huì)有一株是四葉的，西方人認(rèn)為能找到四葉草是幸運(yùn)的表現(xiàn)，在日本則認(rèn)為會(huì)得到幸福，所以又稱“幸運(yùn)草”。

人們對這四片葉子也賦予了含義。有一種說法是：第一片葉子代表希望（hope），第二片葉子表示信心（faith），第三片葉子是愛情（love），而多出來的第四片葉子則是幸運(yùn)（luck）的象征。

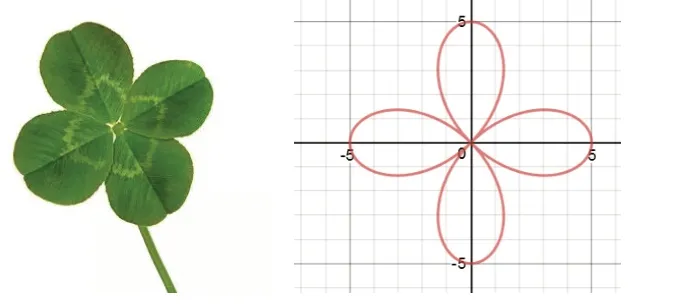
問題1：結(jié)合直線和圓的方程，抽象出來的“四葉玫瑰線”是否也有方程，是否平面曲線都有方程？（四葉玫瑰線的直角坐標(biāo)方程：

問題2：類比方程y=x2與其圖像可以發(fā)現(xiàn)什么？（引導(dǎo)學(xué)生從圖形——數(shù)量角度思考）

問題3：方程F（x，y）=0 的解與曲線C 上的點(diǎn)的坐標(biāo)要具備什么關(guān)系？（一點(diǎn)不多，一點(diǎn)不少）

問題4：曲線與方程的作用是什么？（揭示曲線與方程的本質(zhì)，把曲線的幾何特征轉(zhuǎn)化為數(shù)量關(guān)系（方程），通過代數(shù)運(yùn)算處理已得到的數(shù)量關(guān)系得出曲線的幾何性質(zhì)）

通過問題情境和設(shè)問，材料來自生活，但高于生活，指導(dǎo)學(xué)生利用圖形，分析數(shù)學(xué)問題，建立曲線與方程之間的聯(lián)系，培養(yǎng)學(xué)生的數(shù)學(xué)觀點(diǎn)和數(shù)學(xué)意識，培養(yǎng)學(xué)生用數(shù)學(xué)的視角觀察、感受、認(rèn)識、理解美好世界，培養(yǎng)學(xué)生在日常生活中運(yùn)用數(shù)學(xué)抽象思維方式，促進(jìn)學(xué)生數(shù)學(xué)抽象素養(yǎng)的形成；通過問題2 的探究，建立圖形與數(shù)量的聯(lián)系，初步形成對曲線與方程的認(rèn)識，培養(yǎng)學(xué)生的直觀想象素養(yǎng)的形成；通過問題3 的探究，利用x=2 的圖像和方程|x|=2 的關(guān)系，激發(fā)學(xué)生的好奇心和探索心，同時(shí)引導(dǎo)學(xué)生舉例，通過老師的引導(dǎo)讓學(xué)生感知方程的不同導(dǎo)致曲線的不同，教師再適時(shí)地改編曲線，導(dǎo)致方程的不同。讓學(xué)生多角度體驗(yàn)曲線與方程之間的關(guān)系，概念屬性的歸納——在多則事例的基礎(chǔ)上進(jìn)行屬性的分析、比較、綜合，歸納不同例證的共同特征，引導(dǎo)學(xué)生通過剛才對具體事例觀察、分析，抽象概括共同的本質(zhì)屬性，歸納得出數(shù)學(xué)概念，引出方程與曲線的概念，讓學(xué)生形成嚴(yán)謹(jǐn)?shù)倪壿嬎季S品質(zhì)，促進(jìn)學(xué)生邏輯推理素養(yǎng)的形成；設(shè)計(jì)例題：已知平面上兩點(diǎn)A,B 間的距離為4，平面上一點(diǎn)P 使得PA ⊥PB，求點(diǎn)P 的軌跡方程；通過學(xué)生的自主解答，一題多解，得到點(diǎn)P 的軌跡方程是以AB 為直徑的圓的方程但要挖掉A,B 兩點(diǎn)，讓學(xué)生體會(huì)曲線與方程的對應(yīng)關(guān)系（一點(diǎn)不多，一點(diǎn)不少），探究數(shù)學(xué)運(yùn)算思路，選擇運(yùn)算方法，培養(yǎng)學(xué)生的數(shù)學(xué)運(yùn)算素養(yǎng)。因此，在開展高中數(shù)學(xué)教學(xué)的過程中，不可以僅將教學(xué)內(nèi)容局限于生活層面。對于高中生已經(jīng)具備的數(shù)學(xué)知識，是高中生認(rèn)知和學(xué)習(xí)體驗(yàn)的重要構(gòu)成部分，已經(jīng)成為高中生自身的一種數(shù)學(xué)觀點(diǎn)和數(shù)學(xué)意識。將問題情境過于生活化，很容易致使高中生的思維脫離數(shù)學(xué)知識，使得數(shù)學(xué)知識與問題情境之間相脫離。部分?jǐn)?shù)學(xué)教師往往僅僅在形式上應(yīng)用了問題情境教學(xué)方法，并未將其作為課堂數(shù)學(xué)意識的構(gòu)建途徑和培養(yǎng)高中生數(shù)學(xué)意識的有效策略。因此，數(shù)學(xué)教師在運(yùn)用問題情境教學(xué)方法時(shí)，既需要避免問題稚化，又需要避免形式化。只有這樣，才能夠有效地激發(fā)高中生的數(shù)學(xué)意識，促使高中生自主地參與到問題情境教學(xué)活動(dòng)中。

2.引導(dǎo)高中生自主的發(fā)現(xiàn)問題，升華數(shù)學(xué)意識

基于高中數(shù)學(xué)核心素養(yǎng)的數(shù)學(xué)教學(xué)中，數(shù)學(xué)教師應(yīng)該注重培養(yǎng)高中生的數(shù)學(xué)意識。在數(shù)學(xué)教學(xué)中，數(shù)學(xué)教師應(yīng)該不斷地激發(fā)高中生的好奇心和探索心，通過批判和探究意識，對數(shù)學(xué)知識內(nèi)容產(chǎn)生疑問，并提出問題。在教學(xué)的過程中，應(yīng)該為高中生提供充足的時(shí)間和空間進(jìn)行自主的思考與探索，以此喚起高中生的問題意識。

例如：高中數(shù)學(xué)教師在講《三角函數(shù)的圖像與性質(zhì)》一課時(shí)，可以提出問題：正弦函數(shù)具有的性質(zhì)是什么？通過問題的驅(qū)動(dòng)，高中生很容易展開思維，并對自己提出問題：用什么樣的方法去研究正弦函數(shù)的性質(zhì)？大部分高中生均會(huì)聯(lián)想到自身已經(jīng)學(xué)習(xí)和掌握的冪函數(shù)、指數(shù)函數(shù)以及對數(shù)函數(shù)的學(xué)習(xí)經(jīng)驗(yàn)，發(fā)現(xiàn)同樣可以通過畫圖像的方式，進(jìn)行正弦函數(shù)性質(zhì)的探究。在這一過程中，是通過數(shù)學(xué)現(xiàn)象來啟發(fā)高中生的數(shù)學(xué)意識，這一數(shù)學(xué)現(xiàn)象就是我們需要研究正弦函數(shù)的性質(zhì)，顯然其是數(shù)學(xué)內(nèi)部的知識內(nèi)容，而并非是來源于生活的知識內(nèi)容。

數(shù)學(xué)意識的培養(yǎng)是高中生在學(xué)習(xí)數(shù)學(xué)的過程中自主產(chǎn)生，而不是數(shù)學(xué)教師所傳授的。數(shù)學(xué)教師在培養(yǎng)高中生數(shù)學(xué)意識中所需要做的就是為高中生提供一個(gè)合理的、恰當(dāng)?shù)臄?shù)學(xué)現(xiàn)象，以此作為高中生學(xué)習(xí)的重要切入點(diǎn)。需要注意的是，數(shù)學(xué)教師應(yīng)該不斷地進(jìn)行自我提高和自我完善，并不斷地拓寬教育新思路，以此更好地在基于高中數(shù)學(xué)核心素養(yǎng)中課堂教學(xué)意識的構(gòu)建。

綜上所述，在高中數(shù)學(xué)核心素養(yǎng)的課堂教學(xué)中培養(yǎng)高中生的數(shù)學(xué)意識。數(shù)學(xué)教師應(yīng)該全面地認(rèn)識數(shù)學(xué)意識的重要性，并明確核心素養(yǎng)下對高中生培養(yǎng)的要求，突破傳統(tǒng)的數(shù)學(xué)模式，增強(qiáng)高中生的數(shù)學(xué)體驗(yàn)，豐富高中生的數(shù)學(xué)學(xué)習(xí)經(jīng)驗(yàn)，以此提高高，中生的數(shù)學(xué)意識。