新課改背景下高中數學基本不等式解題技巧研究
湖北省黃石市第七中學 高 明
在高中數學中,學生都知道不等式解題的步驟是“一正、二定、三相等”,但在解題中偏偏就會出現這樣或者那樣的錯誤,丟失不必要的分數。有鑒于此,如何在高中數學課堂教學中有效引導學生完全掌握基本不等式解題技巧就成為我們教師教學的任務。
一、掌握基礎知識
基礎是學習數學的重中之重,如果沒有扎實的學習基礎,在實際學習中就會出現這樣或者那樣的問題。因此,廣大數學教師要重視學生的基礎,幫助他們學習和鞏固基礎內容,有效提升解題能力。在教學過程中,教師可以通過講解基本不等式與幾何性質的關系,使學生了解基本不等式成立的條件,對知識進行有效外延,從而加深對基本不等式相關知識的理解。在基本不等式解題中,湊項法和消元是基礎中的基礎,學生要能夠完全掌握,從而對相關內容進行配湊來解答問題。
例1:(1)若正數x,y滿足x+3y=5xy,則3x+4y的最小值為_____;(2)若x>0,y>0,x+3y+xy=9,則x+3y的最小值為_____。
分析:對于第(1)問,學生應用基本不等式能夠順利完成。對于第(2)問,就稍微有點難度。此時,教師可以引導學生運用消元的方法進行解答。
解:因為x>0,y>0,所以0<y<3,所以當且僅當即y=1,x=3時,(x+3y)min=6。
二、熟練應用所學
在高中數學考試試卷中,大多數的試題具有中等難度,這就有待于學生能力的適度拔高。在日常練習的過程中,教師不妨為學生挑選一些具有代表性的數學試題供他們進行練習,通過精講、精練,促使他們拓寬學習思維,發展自身數學能力。在數學教學中,教師要結合其他知識點,使學生能夠有效應用數學知識,順利解答數學試題。此外,一題多解也有助于學生發展自身數學思維,應用所學知識提升自身能力。
例2:設x,y為實數,若4x2+y2+xy=1,求2x+y的最大值。
在解答這道試題時,筆者要求學生盡可能多想幾種解題方法,發散他們的數學思維。
解法二:令 2x+y=t,∴y=t-2x,代入得 6x2-3tx+t2-1=0,
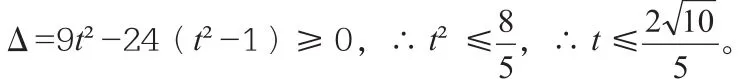
在找到多種解法后,筆者再為學生改變條件,即設x,y為實數,若x2+3xy-1=0,求x+y的最大值。
通過一題多解和變式訓練,大大豐富了課堂教學內容,有效促進了學生的學習效率和質量,適當拔高了他們的課堂學習難度。
三、綜合分析試題
在試卷中,命題人會將基本不等式與其他知識點進行結合作為重要題型來考查學生能力,這就加大了考試難度。對于這種問題,數學教師要認真對待,引導學生掌握解題思路,剖析問題背后的實質,有效提升解答綜合題的能力。在面對綜合試題時,學生不要主動放棄,應當積極回想以往所學的數學知識,根據題目類型和涉及的知識點來找到解題的突破口,增強自身的綜合解題能力,從而拿下綜合試題的大部分,甚至全部分數。
這道試題的難度較大,學生要分步進行求解,回憶以往所學知識,發現是不等式與函數知識點的結合。(1)通過湊項或換元將題干中的函數化簡為滿足基本不等式的形式;(2)運用基本不等式來檢驗其等號成立的條件,若等號取不等則進行第三步,否則直接得出結果;(3)結合函數f(x)的單調性,并運用圖像與性質求出函數最值。針對這種難度較大的數學試題,教師要引導學生從多個角度進行剖析,找到解題思路,尋找解題切入點。
總之,基本不等式在高考中有著非常重要的作用,也是學生學習的難點所在,教師要幫助他們鞏固所學基礎、適度拔高、分析綜合題思路,從而理解和掌握基本不等式的應用,增強獲取數學高分的信心。

