以核心問題引領構建開放的課堂
——以《倒數的認識》為例

江蘇省蘇州高新區實驗小學校 沈 慧

讀2016年《小學數學教師》增刊中潘小明老師帶領的團隊關于“用核心問題引領探究學習”的系列文章，深有感悟。潘老師批判的“教師過度牽引，學生被動接受”的局面還普遍存在。學習潘老師團隊，通過發現學生的真問題引導提煉生成核心問題；構建大空間引領學生圍繞核心問題充分探究、培養學生自主學習意識，讓學生以開放的方式探索未知。我嘗試著上了一節《倒數的認識》（蘇教版六上第二單元內容）。

【教學片段】

（一）核心問題1的提出

片段1：

自學課本后。

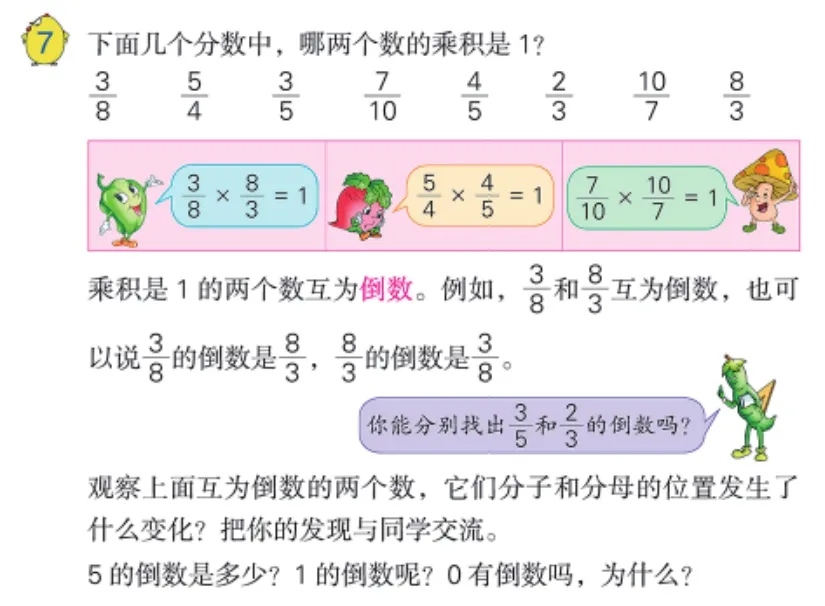
師：誰來解釋“什么是倒數？”

生1：乘積是1的兩個數互為倒數。（教師板書這句話）

師：這句話不難懂，可是結合一些例子就會更好懂。誰來舉例說明？

師：同學們同意嗎？為什么？

生3：因為它們分子、分母倒過來了。

師：倒過來？你們的意思是？（眾生：分子、分母交換位置）

沒有學生表示要補充，再請學生舉例說明，學生仍然以“分子、分母交換位置”作為判斷的依據。

師：你們認為只要分子、分母交換位置的兩個數就互為倒數了，可是書上不是這么說的，你們想想這兩句話是同一個意思嗎？能互相代替嗎？

學生自學課本后的交流碰撞目的之一就是暴露學生真實的認知狀態，從而提煉源于學生的真問題，這就是可以引領課堂的核心問題。

學生自學教材后，雖然一起回答“倒數的意義”能按照書本定義來說，但這里的回答是部分學生還是全體學生的回答？他們能說出概念是源于對概念的理解，還是對一句話的即時記憶？讀懂并不等于理解，理解也不等于會應用。學生讀“乘積是1的兩個數互為倒數”是能夠讀懂的，但再讓他們表達這句話包含的意思就變成了：“分子、分母交換位置的兩個數就互為倒數。”學生的認知是片面的、淺層的。

學生認識偏頗的原因之一是教材例7的舉例都是分數，幾個具體的例子留給學生的印象遠超過一句抽象的概念。原因之二是學生沒有對概念的結語與舉例結合起來深入地思考。發現學生學習中的真問題，接下來怎樣組織教學，讓學生深度理解、掌握概念，并且體會概念學習的方法？

（二）引導對核心問題1的深入剖析

片段2：

學生靜靜地思考，片刻后有學生想到整數，認為整數因為沒有分母，“分子、分母交換位置的兩個數就互為倒數”就不夠妥當，“乘積為1”表達更適合。這時有學生反駁：“整數與它的倒數可以認為是分子、分母交換位置，就像整數與分數相乘可以看成是分數與分數相乘。”她的回答贏得了同學們的掌聲。

思考似乎停頓了一下，這時教師發聲：“交換分子、分母的位置，這種判斷倒數的方法適用于整數、分數。看來我們可以說：分子、分母交換位置的兩個數互為倒數？”

生4：還有小數！

生5：0.5×2=1，0.5和2互為倒數，這時就不適合說分子、分母交換位置……

師：原來小數也可以找它的倒數，誰也來舉例，并說明判斷的理由？

生6:0.125×8=1，所以0.125和8互為倒數。

……

師：同學們對為什么要定義為“乘積是1”，而不是“分子、分母交換位置”深入剖析，對概念中的“兩個數”（在板書這3個字下加著重號）從分數范圍擴展到整數、小數范圍，認識在走向全面、深入。對一個概念的認識就要這樣，盡可能想到它的不同情況，考慮一些特別的例子。

生7：1的倒數還是1，因為1×1=1，1就是1的倒數。

生8:0沒有倒數，因為0乘任何數都等于0。0不可能與一個數的積是1。

源于對核心問題的追問，學生對倒數的認識范圍從分數、整數擴展到了小數，對概念不再是淺層的、形式上的認識，而是深刻理解概念的內涵與外延，對“乘積是1的兩個數……”定義的準確和必要性有了認同。

學生初識概念時的誤解就是學生真實的認知狀態，向學而教，抓住學生真實存在的問題，引導辨析，對誤解的思辨促成了正確、全面的理解。而理解概念要從內涵上逐字逐句推敲，要從外延上考慮它的各種不同情況，包括特例。這些學習概念的經驗與方法，學生在解決問題過程中，在老師的點撥、總結中逐步體會、積累。

（三）核心問題2的提出與解決

片段3：

師：已經認識了怎樣的兩個數互為倒數，我們這節課還有什么可做的呢？

生：怎樣算一個數的倒數。

學生舉例說明求一個分數的倒數只要把分子、分母交換位置；整數可以看成是分母是1的分數，也可以用這樣的方法，由此又得出：一個非0自然數n的倒數就是研究求小數的倒數的方法，有學生根據倒數的定義用1除以這個小數，也有學生想到把小數化成分數，再按分數交換分子、分母的辦法來算，而后一種方法更便捷。

師生交流發現：三類數中，整數、小數都可以先化成分數，再按照分數來求倒數，體現了轉化的思想。

學生們一下子被吸引住了，下課鈴響他們不肯下課，還紛紛表示這節課怎么已經下課了？

研究怎樣求一個數的倒數，學生主動進行分類討論。一個大問題分解成幾個小問題：怎樣求分數的倒數？整數和小數呢？由怎樣求整數的倒數又發現非0自然數倒數的特征，分類討論后又用聯系的眼光發現3類方法中的相同：都可以轉化成分數再求倒數，優化認知結構。學生就這樣不斷地發現問題、解決問題。

最后對“0.999……難道等于1嗎？”的意外之問，看似與本節課無關，卻是實實在在源于學生主動思考問題后發現的問題，這不是在核心問題引領下開放的課堂開出的美麗花朵嗎？

【教學反思】

對核心問題引領下構建的開放課堂，筆者有以下幾點思考：

1.重視學生的真問題，生成核心問題

本節課開始抓住學生的誤解“分子、分母交換位置的兩個數就互為倒數”引導辨析，產生了一連串的問題：“分子、分母交換位置的兩個數就互為倒數”對整數、分數適用，是否適用于所有的數？比如小數？互為倒數的兩個數還有哪些特例？核心問題2也是由學生自己產生、在思辨中產生系列問題，逐步對核心問題有了全面、深入的理解。

問題源于學生，抓住來自學生的真問題，一節課有了研究的主旨，形成思考的磁場。

學生對新學的知識都會有自己的判斷、疑問。比如學習“直線”，學生會誤把生活經驗當作數學概念：把直直的線（數學上的線段）當成是直線；學生在學習《百分數》時自然而然會想到：學了分數為什么還要學百分數？百分數與分數有什么關系？百分數有什么優勢？

思源于疑。抓住學生的所疑所惑順勢而為，解決他們自己產生的問題，學生會以高漲的熱情投入到問題解決中，來自學生的真問題能夠引發學生的探究欲望，學生的真問題也呈現了學生的真實思維，在此基礎上的對話、探究才適切學生的需要。

2.深度解讀教材，提煉核心問題

在《倒數》這一課中有兩個核心問題：倒數能否定義為：“分子、分母交換位置的兩個數互為倒數”？怎樣求一個數的倒數？正好就是本節課的兩個知識點（前一個正好對應倒數的意義）。學生的真問題也正是本節課需要掌握的知識和技能。教師讀懂學生的同時一定要讀懂教材，對教材深度把握才能結合學生情況，提煉出核心問題。

如上例中提到學生學習《百分數》產生的問題，正好涵蓋了百分數的意義、特征、作用，溝通了與舊知識（分數）之間的聯系。教師對教材的深刻理解，才能對這些問題敏銳捕捉、恰當架構，與學生一起“加工”成一節課的核心問題，核心問題的提出離不開教師對教材的深度解讀。

3.核心問題的引領實現開放活力的課堂

相對于傳統課堂中成串的“連問”、簡單的“碎問”的過度牽引，留給學生的是狹小的思維空間，核心問題引領的課堂呈現出小專題式的探究活動，構筑開放的大空間，讓學生的思維真實呈現、交流碰撞、得以完善。

核心問題引領的課堂生機勃勃、充滿著思維的張力。核心問題引領構筑的開放課堂對學生核心素養的發展是全方位的：有序、全面、深入地思考問題的習慣；聯系起來思考問題的方法會讓學生終生受益。學生為解決核心問題而自主生成的一系列子問題，使學生不斷地發現問題、探究問題、再發現再探究……學生發現問題、解決問題的能力得到實實在在的培育。

《倒數》一課，學生不斷地主動發問、思辨論證、聯系比較，課的最后是不想下課，發現一個值得探究的新問題。每一節數學課都這樣上會給學生怎樣的發展？學生對數學有怎樣的情感態度？筆者任教的班級中，不長一段時間后，就有好幾位學困生積極熱情地投入到數學學習中來，其中一位小杰同學從每次考試都不及格蛻變成課堂上眼睛放光、每天都主動交作業請老師面批的孩子。這就是核心問題引領下開放課堂的魅力吧！