初中數(shù)學(xué)“順敞悟”的教學(xué)理解

江蘇省蘇州工業(yè)園區(qū)星洋學(xué)校 楊雪華

教學(xué)實(shí)踐中，我們經(jīng)常會(huì)遇到教師的講解與學(xué)生的理解之間的“不和諧”“喚不醒”“點(diǎn)不燃”，有時(shí)甚至出現(xiàn)“講了幾遍學(xué)生還是不會(huì)”的尷尬，到底是哪個(gè)環(huán)節(jié)出了問(wèn)題？是教得不清？學(xué)得不實(shí)？還是內(nèi)容太難？無(wú)法理解或是無(wú)法掌握？這些現(xiàn)象在教師的工作中時(shí)常出現(xiàn)。筆者調(diào)查后發(fā)現(xiàn)，這些問(wèn)題其實(shí)是教師的“教”與學(xué)生的“學(xué)”的脫節(jié)，數(shù)學(xué)課堂中學(xué)生“理解”“掌握”“應(yīng)用”的前提首先應(yīng)該是“接受”，一種自然而然的對(duì)知識(shí)的“認(rèn)可”。如果學(xué)生的想法“不敞”，教師的教法“不順”，其結(jié)果就是師生間的溝通貌似相通，實(shí)則神離，進(jìn)而大大影響了教學(xué)效果。下面，筆者通過(guò)例子來(lái)談?wù)勥@個(gè)問(wèn)題。

一、“順”模型，“敞”根源——“悟”線段最值轉(zhuǎn)化

《數(shù)學(xué)課程標(biāo)準(zhǔn)》指出：數(shù)學(xué)課程內(nèi)容要符合學(xué)生的認(rèn)知規(guī)律，要貼近學(xué)生的實(shí)際，有利于學(xué)生體驗(yàn)與理解、思考與探索，教師教學(xué)應(yīng)該以學(xué)生的認(rèn)知發(fā)展水平和已有的經(jīng)驗(yàn)為基礎(chǔ)，注重啟發(fā)式和因材施教。

1.原題呈現(xiàn)

問(wèn)題：如圖（1），已知A、B是兩個(gè)定點(diǎn)，在定直線l上找一動(dòng)點(diǎn)M，在平面內(nèi)找一動(dòng)點(diǎn)N，直線MN的方向確定（即直線MN與直線l右側(cè)部分相交所得的銳角為α），且MN等于定長(zhǎng)d，使AN+NM+MB最小。

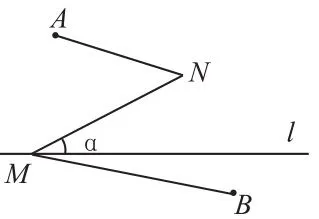
圖（1）

分析：要求AN+NM+MB的最小值，這是動(dòng)線段的最值問(wèn)題，因?yàn)镸N等于定長(zhǎng)d，所以只需求AN+MB的最小值即可。于是將三條動(dòng)線段的最值問(wèn)題轉(zhuǎn)化為兩條動(dòng)線段的最值問(wèn)題。

那么怎樣解決呢？分析到此處，學(xué)生可能還是難以突破，教師要順著學(xué)生的思路，提出關(guān)鍵一問(wèn)：“線段怎么會(huì)運(yùn)動(dòng)的？”得出本題的實(shí)質(zhì)，即為“點(diǎn)動(dòng)線動(dòng)”，轉(zhuǎn)化為動(dòng)點(diǎn)最值問(wèn)題，還原出數(shù)學(xué)問(wèn)題的本質(zhì)。此時(shí)如果學(xué)生還有不解，我們可以順著學(xué)生已經(jīng)認(rèn)可的“點(diǎn)動(dòng)”最值，引出如下兩個(gè)模型。

2.順導(dǎo)敞思

聯(lián)想生成1——“將軍飲馬”模型：如圖（2），圖（3），在定直線l上找一個(gè)動(dòng)點(diǎn)P，使動(dòng)點(diǎn)P到兩個(gè)定點(diǎn)A與B的距離之和最小，即PA+PB最小。

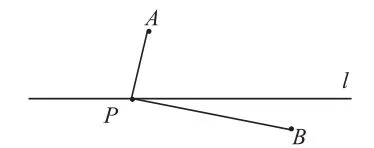
圖（2）

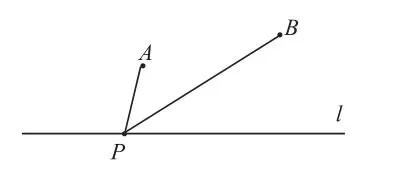
圖（3）

分析：如圖（2），連接AB交l于點(diǎn)P，即為所求的直線l上的點(diǎn)。如圖（3），作點(diǎn)A關(guān)于直線l的對(duì)稱點(diǎn)A′，連接A′B交l于點(diǎn)P，即為滿足條件的直線l上的點(diǎn)。這個(gè)“兩點(diǎn)一線”模型，學(xué)生應(yīng)該沒(méi)有太大問(wèn)題。

聯(lián)想生成2——“行船運(yùn)貨”模型：如圖（4），已知A、B是兩個(gè)定點(diǎn)，在定直線l上找兩個(gè)動(dòng)點(diǎn)M與N，且MN等于定長(zhǎng)d（動(dòng)點(diǎn)M位于動(dòng)點(diǎn)N左側(cè)），使AM+MN+NB最小。

如圖（4），要求三條線段AM+MN+NB的最小值，而這三條線段恰好構(gòu)成一條折線，學(xué)生的第一想法是運(yùn)用“折線大于直線”思想，連接AB即為最小值；但畫(huà)圖發(fā)現(xiàn)AB與l只有一個(gè)交點(diǎn)，這個(gè)交點(diǎn)是M還是N呢？學(xué)生出現(xiàn)思維的矛盾。再進(jìn)一步，直線l上需要找兩個(gè)動(dòng)點(diǎn)M與N，但這兩個(gè)動(dòng)點(diǎn)是相互牽制、彼此影響的，不過(guò)保持MN等于定長(zhǎng)d（且動(dòng)點(diǎn)M位于動(dòng)點(diǎn)N左側(cè)），也就是當(dāng)動(dòng)點(diǎn)M確定下來(lái)，動(dòng)點(diǎn)N也會(huì)隨之向右平移d個(gè)單位確定下來(lái)。“順藤摸瓜”，教師將學(xué)生的思路很自然地引導(dǎo)到了“平移”。學(xué)生認(rèn)可“平移”后，思維基本敞開(kāi)，原問(wèn)題便可轉(zhuǎn)化為線段AM+NB的最小值。如圖（5），將定點(diǎn)A沿著定直線l的方向向右平移d得到點(diǎn)C，構(gòu)造出平行四邊形ACNM，就有AM+NB=CN+NB，于是要求AM+NB最小，只需求CN+NB最小。連接CB，與定直線l的交點(diǎn)N即為所要尋找的點(diǎn)N，而點(diǎn)M只需將點(diǎn)N向左平移d個(gè)單位即可找到，此時(shí)AM+MN+NB的最小值問(wèn)題便迎刃而解了。

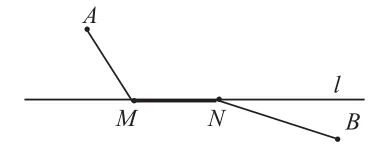
圖（4）

圖（5）

3.感悟深究

如圖（6），已知A、B是兩個(gè)定點(diǎn)，在定直線l上找兩個(gè)動(dòng)點(diǎn)M與N，且MN等于定長(zhǎng)d（動(dòng)點(diǎn)M位于動(dòng)點(diǎn)N左側(cè)），使AM+MN+NB最小。用類比的思想，讓學(xué)生自行解決。

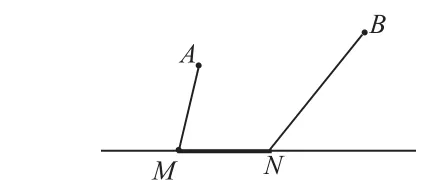
圖（6）

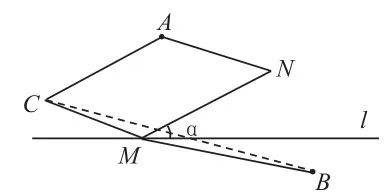
圖（7）

4.問(wèn)題反芻，領(lǐng)悟生成

現(xiàn)在我們重新回到本文開(kāi)始的問(wèn)題探究。如圖（1），點(diǎn)A、B是定點(diǎn)，在定直線l上找一動(dòng)點(diǎn)M，在平面內(nèi)找一動(dòng)點(diǎn)N，直線MN的方向確定（即直線MN與直線l右側(cè)部分相交所得銳角為α），且MN等于定長(zhǎng)d，使AN+NM+MB最小。

學(xué)生有了前面的鋪墊和積累，分析解決就會(huì)游刃有余了。如圖（7），將定點(diǎn)A沿著NM的方向，向左下方平移d個(gè)距離得到點(diǎn)C，構(gòu)造出平行四邊形ACMN，就有AN+MB=CM+MB，要求AN+MB的最小值，只需求CM+MB的最小值，順利將本問(wèn)題轉(zhuǎn)化為了如圖（2）的問(wèn)題。連接CB，與定直線l的交點(diǎn)M即為所要尋找的點(diǎn)M，再將點(diǎn)M作相應(yīng)平移即可找到點(diǎn)N，此時(shí)AN+NM+MB最小，且等于d+CB。

二、“順”學(xué)識(shí)，“敞”心智——“悟”教學(xué)真與實(shí)

1.原題呈現(xiàn)

問(wèn)題：已知點(diǎn)P是拋物線y=ax2+c上一個(gè)動(dòng)點(diǎn)，且點(diǎn)P到直線y=－2的距離始終等于PO（O為坐標(biāo)原點(diǎn)），則該拋物線的解析式為_(kāi)_________ 。

2.順導(dǎo)敞思，真實(shí)面對(duì)

教學(xué)實(shí)踐發(fā)現(xiàn)，學(xué)生讀題后對(duì)拋物線解析式y(tǒng)=ax2+c感到困惑，參數(shù)a、c不確定導(dǎo)致無(wú)從下手。教師讀題順勢(shì)而為，“既然a、c不確定，那該怎樣處理呢？”順引出“分類討論”，畫(huà)出可能情形。

舉例如下：如圖（8），當(dāng)點(diǎn)P運(yùn)動(dòng)到拋物線的頂點(diǎn)時(shí)，點(diǎn)P到原點(diǎn)O的距離與點(diǎn)P到直線y=-2的距離一定不相等。此種情況可排除。

如圖（9），教學(xué)時(shí)引導(dǎo)學(xué)生找出反例。當(dāng)點(diǎn)P運(yùn)動(dòng)到拋物線與直線y=-2的兩個(gè)交點(diǎn)時(shí)，此時(shí)點(diǎn)P到原點(diǎn)O的距離與點(diǎn)P到直線y=-2的距離一定不相等。此種情況也可排除。

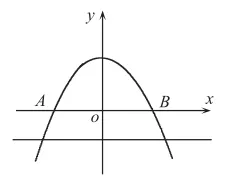
圖（8）

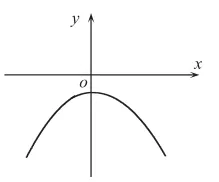
圖（9）

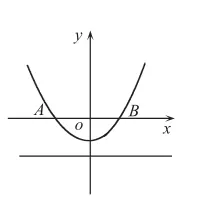
圖（10）

綜合考慮后，得出只有圖（10）符合題意。

解析：設(shè)點(diǎn)P坐標(biāo)為(x，y)，則PO2=x2+y2。可得點(diǎn)P(x，y)到直線y=-2的距離d=|y+2|，由題意得d2=PO2，即：x2+y2=|y+2|2，即x2+y2=y2+4y+4，得所以該拋物線解析式為

筆者倡導(dǎo)的數(shù)學(xué)課堂教學(xué)的“順敞悟”的實(shí)質(zhì)是順學(xué)情、順學(xué)力、順學(xué)生的心智，敞基礎(chǔ)、敞思維、敞學(xué)生已有的認(rèn)知和經(jīng)驗(yàn)，探索一種純自然的、質(zhì)樸的教學(xué)體驗(yàn)，接受、認(rèn)可、理解、內(nèi)化、銘刻乃至以不變應(yīng)萬(wàn)變的運(yùn)用。師生雙方的教學(xué)活動(dòng)猶如“心有靈犀一點(diǎn)通”。這一“點(diǎn)”正是四兩撥千斤，使學(xué)生能走出疑惑、跳出迷局、學(xué)的輕松、學(xué)出成效。筆者愿和各位讀者共同探索，努力實(shí)現(xiàn)“內(nèi)容清楚、過(guò)程簡(jiǎn)單、思維順敞、感悟真切、效果顯著”的初中數(shù)學(xué)高效課堂。