以一道最值問題的推廣來培養學生的核心素養
江蘇省常州市第五中學 趙艷芝
在教學過程中,讓學生解數學題是家常便飯。但不能只是簡單解題,有時候解完題后再多問幾個為什么,或許會“別有滋味”,在我們沉浸于“原來如此”的喜悅的同時,可以在解題的思路更新和能力創新方面得到真實的歷練。最近在學習向量的教學過程中,就遇到了一道題,在我的引導與鼓勵下,學生嘗試著對問題進行變式推廣。
一般情況下,向量問題有三種處理思路,即直接法、坐標法和基向量轉換法。學生考慮到這道題沒有給出向量長度和夾角,從而用定義直接處理的思路就否定了;因為題目中有垂直,故在處理時,學生自然首選坐標法。以A為原點、AC為x軸建立平面直角坐標系,其解題過程如下:
因BC的直線方程為故而設
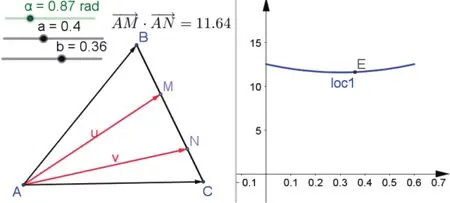
本來題目做到這兒就可以結束了,但有同學發現時,線段MN恰好處于線段BC的中間位置(MN的中點即為BC的中點);而或1時,MN偏向線段BC的一側(有一個端點與線段BC的端點重合),加之本題的背景是等腰直角三角形,從圖形的對稱性上也能解釋特殊法的合理性,于是有同學就想:這樣的結論是否可以推廣到一般的等腰三角形中呢?
接下來,我用GeoGebra軟件做了推廣驗證(如下圖),改變M點的位置,得到數量積的計算值;而以M點的橫坐標、數量積的計算值分別為橫縱坐標構造E點后,以M點為主動點、E點為從動點構造軌跡。軌跡圖像有力地支持了學生的猜想,而這樣的圖像特性(在中點處取得最小值、在端點處取得最大值)恰與角的大小無關,真是“有圖有真相”,這一驗證讓學生頓時信心百倍。
回首這道題的解體過程,經過討論學生發現,之所以沒證出來,關鍵是題設字母設得不合理,MN這一定值不應設為絕對值,而應設為相對值(可設為這樣計算起來應該方便些。再者,考慮到書上有關于三點共線的一個結論:點在直線上,則有且于是在我的鼓勵下,學生修正了原來的解法,整理推廣過程如下:
MN在BC上,所以有
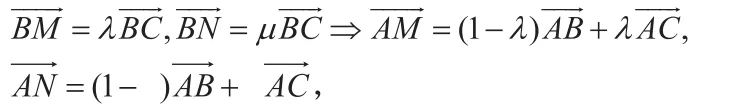
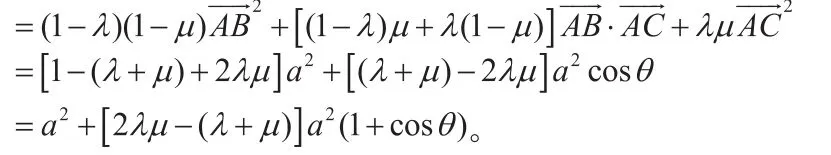
題目解到這兒已是不易,接下來往哪兒走卻很關鍵。在此提醒學生冷靜冷靜,回頭看,學生發現題中有M、N兩個動點,它們分別對應著變量和,這樣四個字母中就只有和是變量了,于是只需要重點考慮即可,結合兩限制條件可以想到消元,于是想到干脆提取出來設一個函數進行研究:
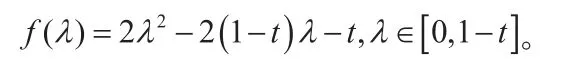
這次探究經歷于學生而言,“得”遠遠大于“失”,“失”的是寶貴的時間(過程很費周折),“得”的卻是對數學解題滿滿的體驗:首先是對數學解題的全新思考。通過題目特殊位置、特殊值的分析,猜想一般化的結論,繼而證明猜想,從而發現有關數量積范圍的推廣命題,我覺得這才是日常做數學的感覺。其次,數學解題需要有一定的想象和思維發散。在推廣過程中鍛煉了學生的發散思維,使學生對問題的本質認識更加清晰,事實上,原題中即相當于推廣題中的這樣只要將推廣題的證明稍作改動,就得到原題的基向量的證法。最后,數學解題需要明辨方向、梳理思路。原來學生之所以會陷入困境,主要還是忽視了書上的三點共線性質,而有了這次經歷,下次再遇到含多個字母的試題,相信學生會更有底氣、有毅力。

