函數(shù)知識在日常生活中的應(yīng)用分析

李浩涵

摘 要：在高中數(shù)學(xué)的學(xué)習(xí)中，函數(shù)概念是眾多數(shù)學(xué)概念中的重點(diǎn)之一，經(jīng)過300年的研究與發(fā)展，廣大學(xué)者已經(jīng)分別從不同的角度對函數(shù)知識進(jìn)行分析，包括集合角度、代數(shù)角度、幾何角度等等，這也使函數(shù)知識得到了快速的完善與發(fā)展，本文則是從函數(shù)知識在日常生活中的應(yīng)用的角度加以闡述，分析一次函數(shù)、二次函數(shù)、三角函數(shù)、指數(shù)函數(shù)以及對數(shù)函數(shù)在生活中的具體應(yīng)用。

關(guān)鍵詞：函數(shù)知識;日常生活;例題解析

函數(shù)是高中數(shù)學(xué)的重要組成部分，與之同時(shí)，在日常生活中函數(shù)知識也得到了廣泛的應(yīng)用[1]。函數(shù)知識在生活中應(yīng)用，主要是指將生活中的問題運(yùn)用變量關(guān)系表達(dá)出來，分析問題中各個(gè)元素之間的關(guān)系，這種關(guān)系運(yùn)用函數(shù)的方式表達(dá)出來，再通過該函數(shù)的性質(zhì)、圖像等基礎(chǔ)知識來實(shí)現(xiàn)解決問題的目的[2]。該思想能夠?qū)⑷粘Ｉ钪械膯栴}變復(fù)雜為簡單、變抽象為具體，進(jìn)而解決問題。函數(shù)有很多種類，一般分為一次函數(shù)、二次函數(shù)、三角函數(shù)、指數(shù)函數(shù)以及對數(shù)函數(shù)，本文就分別舉例說明這些函數(shù)在生活中的具體應(yīng)用與重要作用。

1.函數(shù)的相關(guān)概念

1.1函數(shù)的定義

函數(shù)的傳統(tǒng)定義為[3]：一般來講，在一個(gè)不斷地變化形勢中，假設(shè)兩個(gè)變量分別為x和y，如果對于任意一個(gè)x都有唯一一個(gè)y與之對應(yīng)，那么就可以將x稱作是自變量，將y視作是x的函數(shù)。函數(shù)的近代定義為：有兩個(gè)非空的數(shù)集，分別為A和B，若根據(jù)一種已定的對應(yīng)關(guān)系f，能夠使A中的任何一個(gè)元素x，在B中都有唯一一個(gè)確定的y與之對應(yīng)，那么就將映射f稱作是集合A到集合B的一個(gè)函數(shù)。

1.2函數(shù)的表現(xiàn)方式

函數(shù)的表示方式主要分為下面幾種[4]：（1）解析式法，該方法是運(yùn)用等式將兩個(gè)變量的函數(shù)關(guān)系表現(xiàn)出來的一種方法，具有準(zhǔn)確、清晰等優(yōu)點(diǎn)，但是卻存在運(yùn)算復(fù)雜等缺點(diǎn)，一般形式為：y=ax+b。（2）列表法，該方法是運(yùn)用列表將兩個(gè)變量的函數(shù)關(guān)系表現(xiàn)出來的一種方法，具有直觀讀取自變量與函數(shù)值的優(yōu)點(diǎn)，但是卻存在無法展示函數(shù)全貌的局限的缺點(diǎn)。（3）圖像法，該方法是運(yùn)用圖像將兩個(gè)變量的函數(shù)關(guān)系表現(xiàn)出來的一種方法，能夠?qū)⒑瘮?shù)關(guān)系直觀、形象的展示出來，但是圖像只能呈現(xiàn)出相近的數(shù)值關(guān)系。（4）語言敘述法。該方法是運(yùn)用語言將兩個(gè)變量的函數(shù)關(guān)系表現(xiàn)出來的一種方法，在數(shù)學(xué)題目中的應(yīng)用并不多。

2.函數(shù)知識在生活中的應(yīng)用分析

函數(shù)在數(shù)學(xué)家族中是重要的家庭成員，并且在日常生活中也是隨處可見。一次函數(shù)能夠解決租車問題、二次函數(shù)能夠解決銷售問題、三角函數(shù)能夠解決停車場問題、指數(shù)函數(shù)以及對數(shù)函數(shù)能夠解決人口問題以及儲蓄問題等，這些函數(shù)都能夠?qū)θ粘Ｉ钪心承﹩栴}進(jìn)行完美的解決，能夠?qū)⒆匀唤缰胁煌淖兞恐g表示出特定的關(guān)系，對我們的生活具有必不可少的作用。

（1）一次函數(shù)對租車問題的解決

一次函數(shù)是函數(shù)知識的基礎(chǔ)，也在日常生活中最常見，例如購物總價(jià)與購物數(shù)量呈現(xiàn)出一次函數(shù)關(guān)系，租用車輛經(jīng)費(fèi)與車輛數(shù)量呈現(xiàn)出一次函數(shù)關(guān)系等等，具體如下：

例題：某學(xué)校組織活動租用車輛，經(jīng)費(fèi)在2300元內(nèi)，共有234個(gè)學(xué)生與6個(gè)老師坐車，每輛車至少有一個(gè)老師，現(xiàn)有兩種客車，甲客車能夠裝載45人，租金為400元，乙車能夠裝載30人，租金為280元，則最經(jīng)濟(jì)的租車方案應(yīng)怎樣選擇？

解題分析：共有240人需乘車，客車總數(shù)不能少于240/45，則需租用6輛車。設(shè)租甲車x輛，車費(fèi)為Y，則兩者間可以呈現(xiàn)出函數(shù)關(guān)系：Y=400x+280（6-x）=120x+1680，而Y≦2300，則x≦31/6，即x≦5。同時(shí)要確保全部師生有座位，則x要大于等于4，因此有兩種方案，一種是甲車4輛，乙車2輛，一種是甲車5輛，乙車1輛，而Y與x呈現(xiàn)出正比關(guān)系，所以x越小，Y越小，因此應(yīng)該選擇方案一，甲車4輛，乙車2輛，最經(jīng)濟(jì)。

（2）二次函數(shù)對銷售問題的解決

二次函數(shù)常用于一個(gè)變量隨著另一個(gè)變量均勻變化時(shí)而出現(xiàn)變化越來越快的情況中，例如細(xì)胞分裂的數(shù)量與時(shí)間呈現(xiàn)出二次函數(shù)關(guān)系，自由落體速度與下落時(shí)間呈現(xiàn)出二次函數(shù)關(guān)系，導(dǎo)彈爆炸路線也呈現(xiàn)二次函數(shù)，還可以應(yīng)用在銷售問題中，如下：

例題：每逢過年過節(jié)期間，人們對于鮮魚的需求量大量上漲，某養(yǎng)殖戶采用排水的方式降低捕魚成本來應(yīng)對市場需求，先后不間斷排水20天。經(jīng)研究發(fā)現(xiàn)，降低水位的天數(shù)與鮮魚銷售存在下面的關(guān)系，設(shè)捕撈x天，鮮魚銷售單價(jià)為20元/kg，單位捕撈成本為（5-x/5）元/kg，捕撈量為（950-10x）kg。則假定這些天都沒有其他損失，鮮魚也能夠當(dāng)天售罄，則求排水第幾天該養(yǎng)殖場的收入最高？

解題分析：由于當(dāng)天收入=日銷售額-日捕撈成本，則y=20（950-10x）-（5-x/5）（950-10x）=-2（x-10）2+14450，則因?yàn)閤的取值在1到20之間，而當(dāng)1≦x≦10時(shí)，函數(shù)為增函數(shù)，當(dāng)10≦x≦20時(shí)，函數(shù)為減函數(shù)，因此當(dāng)x=10時(shí)，y取得最大值，即y=14450元。

（3）三角函數(shù)對停車場問題的解決

日常生活中經(jīng)常會出現(xiàn)三角形，而三角函數(shù)也由此而生。例如建筑施工過程中的高度測量需要運(yùn)用到三角函數(shù)知識，航海行程需要運(yùn)用到三角函數(shù)知識，檢測房屋建造是否合理需要運(yùn)用到三角函數(shù)知識，三角函數(shù)還可以應(yīng)用在停車場問題的解決中，如下：

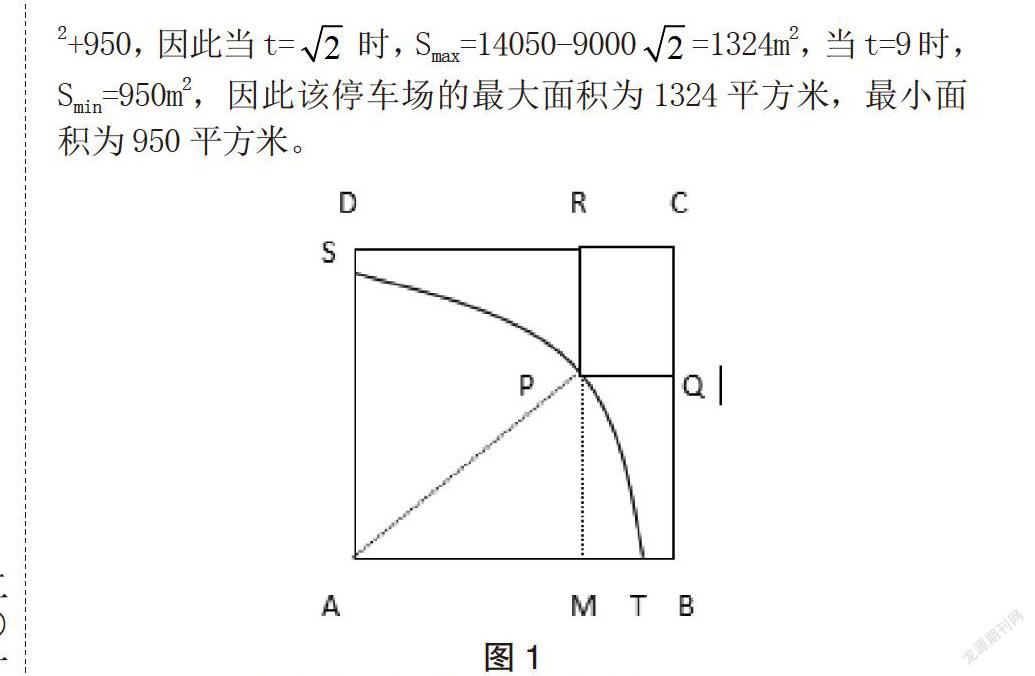
例題：如圖1，ABCD是一塊邊長為100m的正方形土地，其中，ATPS是半徑為90m的扇形小山，P是弧TS上一點(diǎn)，其余部分都為平整土地，現(xiàn)在某開發(fā)商想在該土地上創(chuàng)建一個(gè)邊落在BC與CD上的長方形停車場PQCR，則該停車場的最大面積與最小面積分別為多少？

解題分析：設(shè)∠PAB=x°（0<x<90），延長RP交于AB于M，則AM=90cosx，MP=90sinx，所以PQ=AB-AM=MB=100-90cosx，PR=MR-MP=100-90sinx，因此矩形PQCR的面積為S=PQ×PR=（100-90cosx）（100-90sinx）=10000-9000（sinx+cosx）+8100sinx·cosx，令t=sinx·cosx（1<t≦），則sinx·cosx=（t2-1）/2，因此S=10000-9000t+8100（t-10/9）2+950，因此當(dāng)t=時(shí)，Smax=14050-9000=1324m2，當(dāng)t=9時(shí)，Smin=950m2，因此該停車場的最大面積為1324平方米，最小面積為950平方米。

圖1

（4）其他函數(shù)在日常生活中的應(yīng)用

除去一次函數(shù)、二次函數(shù)、三角函數(shù)之外，指數(shù)函數(shù)與對數(shù)函數(shù)也是數(shù)學(xué)函數(shù)知識的重要組成部分，而指數(shù)函數(shù)與對數(shù)函數(shù)呈現(xiàn)出正反函數(shù)的關(guān)系，兩者在生活中的應(yīng)用也非常相似，例如指數(shù)函數(shù)與對數(shù)函數(shù)在存款利率問題、路線規(guī)劃等問題中都能夠得到廣泛應(yīng)用，因?yàn)檫@些問題都呈現(xiàn)出非常明顯的指數(shù)關(guān)系或是對數(shù)關(guān)系。例如日常生活中，人們會將除去日常花銷之外的資金儲存在銀行中，而銀行儲蓄的利息計(jì)算也是人們關(guān)注的重點(diǎn)。如果一個(gè)人將本金m存入銀行中，而銀行每期的利潤為r，則此人將這些資金儲存x期后再取出，將得到本息和y=m（1+r）x。又或者是通過大數(shù)據(jù)測算網(wǎng)購習(xí)慣，運(yùn)用對數(shù)函數(shù)與指數(shù)函數(shù)對消費(fèi)者的購買產(chǎn)品進(jìn)行統(tǒng)計(jì)，再綜合相關(guān)信息了解消費(fèi)者的購買習(xí)慣，以便為消費(fèi)者推薦所需商品;與之同時(shí)，通過對交通流量測算，運(yùn)用對數(shù)函數(shù)或者指數(shù)函數(shù)對相關(guān)數(shù)據(jù)計(jì)算與分析，能夠提前引導(dǎo)行人規(guī)劃合理路線等。運(yùn)用函數(shù)解決此類問題能夠大大減少工作人員的工作量，為人們的日常生活帶來了很大的便利。

結(jié)束語：函數(shù)知識在日常生活中的應(yīng)用，主要是將日常生活中的問題抽象成數(shù)學(xué)問題，分析已知量以及未知量，找到兩者之間的關(guān)系，并運(yùn)用函數(shù)將這種關(guān)系呈現(xiàn)出來，再經(jīng)過具體的運(yùn)算以及推理將問題完美的解決。函數(shù)分為多個(gè)種類，每種函數(shù)都在日常生活中得到了有效的應(yīng)用，一次函數(shù)能夠表示購物總價(jià)與購物數(shù)量之間的關(guān)系，并且能夠解決租用車輛問題;二次函數(shù)能夠表示細(xì)胞分裂的數(shù)量與時(shí)間之間的關(guān)系，并且能夠應(yīng)用在銷售問題的解決中;三角函數(shù)能夠解決建筑施工過程中的高度測量問題以及檢測房屋建造是否合理，同時(shí)還能夠應(yīng)用在停車場問題中;指數(shù)函數(shù)與對數(shù)函數(shù)這對正反函數(shù)都能夠應(yīng)用在存款利率問題、規(guī)劃路線等問題的解決中。

參考文獻(xiàn)

[1]蔡宇洋.談高中數(shù)學(xué)函數(shù)學(xué)習(xí)的幾點(diǎn)體會[J].數(shù)學(xué)學(xué)習(xí)與研究，2018（20）：149.

[2]盧彥青.淺談高中數(shù)學(xué)知識在日常生活中的應(yīng)用[J].科學(xué)咨詢（科技·管理），2018（10）：119.

[3]何同舟.高中基本初等函數(shù)教學(xué)問題研究[J].陜西師范大學(xué)，2018（10）：84.

[4]卜芳.函數(shù)極值知識在生活中的應(yīng)用[J].科教文匯（上旬刊），2012（10）：84+89.