巧用圖形變換培養空間思維能力

黃秀科 徐花

摘要：本文通過初中七年級三種應用題類型的解題方法，探索方程建模的培養方法與途徑，旨在多種多樣的課堂教學方法中，歸納出適合學生學習實際和效果明顯的教學技巧，給廣大教學一線的初中數學教師提供學習和借鑒.

關鍵詞：初中;數學;教學

吃透教材，探究新課程理念，加大課改力度，創設新型的教學模式，提升數學空間想象能力。

一、背景

2017年春季學期開始，學校委托我在3年內培養新入職的年輕教師徐花，快速成長為教學能手，2018年11月，我們師徒二人受邀參加右江區在片區龍頭學校百色市五中舉行的《青年教師匯報課》上亮相一節公開課。我兩設計了一節“借助平移、翻折、旋轉的圖形變換理解三角形全等”的探究課。課前準備充分，展示課上師生互動活躍，學生的發散思維表現得淋漓盡致，得到了現場專家和教師的認可。現將本節課的設計和領悟整理成文，以便和同行們參考交流。

全等三角形的教學是八年級上冊內容，是初中生進入幾何推理的入門，是幾何教學中圖形辨認的啟蒙。

二、目標

本節課是在學生學完全等三角形“SAS、ASA、AAS、SSS”四個判定的基礎上加以提升的綜合課，其目的是培養“空間思維”這一數學核心素養的能力，讓教學從感性認知提升到理性認識，挖掘、突破教學難點。

三、教學設計環節

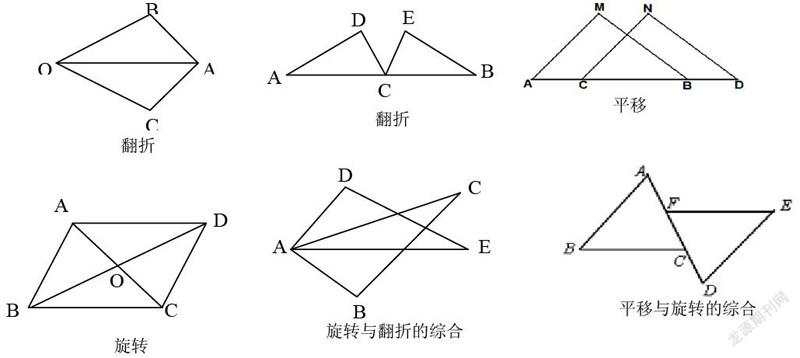
1.用平移、翻折、旋轉的圖形變換直觀識別常見的全等三角形圖形，打開空間想象引入課堂。

課堂展示方式：課堂中讓學生合作討論、口頭描述變換方式，教師利用幾何畫板演示，在實踐課中讓學生動手操作體驗幾何畫板加深理解，從感性認知中打開“空間想象思維”的數學核心素養。

2.以條件探索的形式匡實基礎，培養空間想象力。實例展示

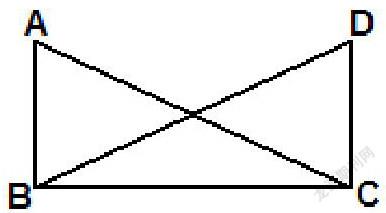
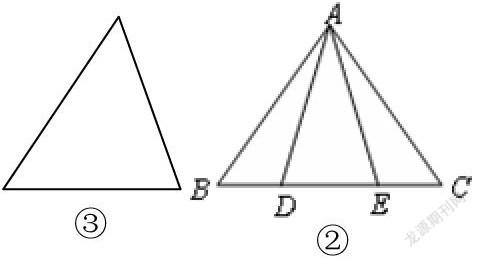
例1?如圖，

（1）猜猜圖中可能有幾對三角

形全等;

（2）在△ABC和△DCB中，

AC=DB，還需增加一個

條件，可使△ABC ≌ △DCB（不再增加任何字母與輔助線）。

（3）用平移、翻折或旋轉的圖形變換描述把△ABC與 △DCB疊合的過程。

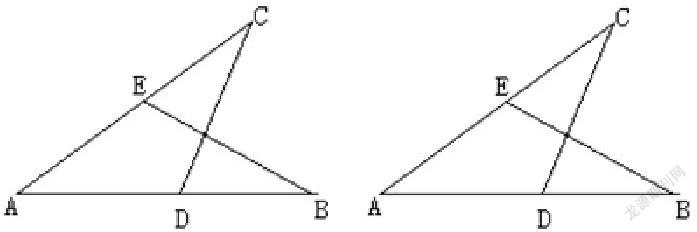
例2?如圖

猜猜圖中可能有幾對三角形全等;

（1）能用字母表示可能全等的三角形有幾對？（用平移、翻折或旋轉的圖形變換想象并加以描述）

（3）已知在△ABE和△ACD中，AB = AC，要使△ABE ≌ △ACD，還需添加一個條件，這個條件可以是?。

反思：該例題設計的用意

（1）突出幾何學習的常用方法→猜測結論，再加以論證;

（2）利用圖形變換培養識圖能力;

（3）在教材傳統教法上推出新的理念，利用多種手段從不同角度解決問題;

（4）背景設計打破常規、新穎，增加課的趣味性。

3.以嘗試加實踐的課堂模式，尋找證明思路，培養三角形全等證明的數學建模核心素養。示例展示

試一試

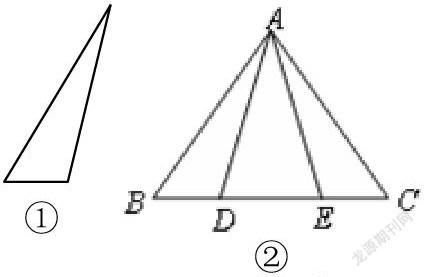
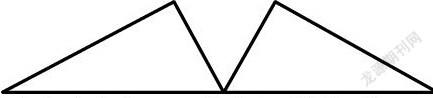
例：（1）利用平移、翻折或旋轉的知識把兩個圖①拼接成圖②（觀察圖②中兩個圖①所在的位置）

（2）結合圖②編寫一道與

三角形全等有關的證明題。

仿上例：（1）例用平移、翻折或旋轉的知識把兩個圖③拼接成圖②（描述拼圖過程）

（2）結合圖②再編寫一道與三角形全等有關的證明題

效果：（1）打開了學生的“發散思維”這一數學核心素養;

（2）共享資源豐富多彩;

（3）躍躍欲試、合作分享養成習慣;

（4）合作、分享等德育教育融入課堂;

（5）例題難易梯度科學合理（由直觀拼圖層層深入轉向邏輯推理）。

4.以動手實驗操作題型收尾課堂，體現對知識的認知由感知動手實踐提升到理論成果的數學核心素養。

示例?體驗、合作完成題

將兩塊（含60°角）相同的三角板如圖擺放，兩斜邊在同一直線上，60°角的頂點拼接在同一點上。

①：探究兩直

角頂點與60°角頂

點所圍成三角形的形狀（在圖中標上字母后說明理由）;

②：將①中右邊三角板沿斜邊向左平移到直角頂點重合后停止，畫出平移停止后的圖形。判斷重合部分三角形的形狀（說明理由）;

③繼續探究?重合部分三角形面積與其中一塊三角板面積的數量關系（說明理由）

②、③的圖?→

要求學生動手畫圖

反思：此題設計由淺入深，知識遷移自然。第一問讓學生找到解題的方向為第二問埋下伏筆;第二問難度是審清題意后準確的畫出相應圖形，只要圖形出現，解法思路自然柳暗花明;第三問繼續探究轉入面積，體現了“知識多元化”的數學核心素養。