隨機車流作用下鋼箱梁斜拉橋疲勞壽命評估分析
李少軍 孫一嬋
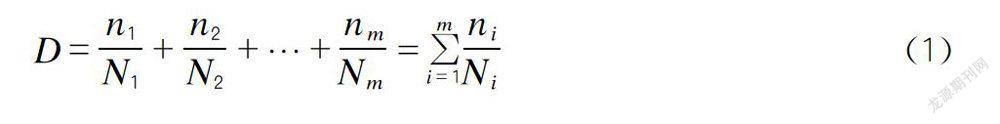

摘要:為了對大跨度鋼箱梁斜拉橋在隨機車流作用下的疲勞壽命進行評估,文章采用ANSYS有限元軟件建立了東平河大橋跨中主梁標準節段殼單元有限元模型,通過計算分析得到了關鍵U肋位置的兩種焊縫細節的應力影響面函數;參考某大橋動態稱重系統的統計數據,建立了隨機車流模型;通過數值模擬方法獲取了鋼箱梁細節的應力時程響應,對大橋關鍵位置焊縫細節的疲勞性能進行了研究,得出了一些有意義的結論。
關鍵詞:橋梁工程;隨機車流;應力時程;疲勞損傷;疲勞壽命
中圖分類號:U448.213 文獻標識碼:A DOI:10.13282/j.cnki.wccst.2019.08.023
文章編號:1673-4874(2019)08-0084-05
0引言
隨著我國經濟的發展,城市交通量不斷增加,導致大橋承受的交通荷載日益增長,然而大跨度鋼橋在隨機車流荷載的反復作用下,結構構件的應力隨之循環變化并不斷累積產生疲勞損傷破壞,將嚴重威脅大跨度鋼橋的運營安全和使用壽命。因此合理評估大跨度鋼橋結構及關鍵構件的疲勞性能成為橋梁結構全壽命周期性能評估的重要環節。
大跨度斜拉橋一般采用具有較好抗風性能的流線型扁平鋼箱梁結構,其正交異性橋面板在車輛荷載的反復作用下容易產生疲勞損傷。隨著運營時間的增長,疲勞損傷逐漸累積,在超過疲勞抗力后將會突然發生斷裂破壞,甚至導致橋梁結構垮塌。因此,開展鋼箱梁斜拉橋的疲勞壽命和疲勞可靠度評估具有重要的研究意義,本文基于數值模擬對東平河大橋開展了疲勞壽命評估的研究。
1疲勞壽命評估理論
由于車輛在橋面上行駛,橋面板通常受到變幅荷載的作用,為了確定常幅疲勞強度和變幅疲勞強度之間的關系,需要了解疲勞累積損傷理論。國內外有很多學者對這一問題進行了大量研究,在眾多成果中,目前應用最為廣泛的是PaImgren與Miner的研究成果。PaImgren-Miner線性損傷累積理論認為,變幅應力循環Si產生的疲勞損傷疊加構成總的疲勞損傷,計算式為:
式(1):ni為應力循環次數;Ni為S-N曲線中對應常幅應力幅值為Si的應力總循環次數。Miner準則中假定D≥1時,構件將發生疲勞破壞。
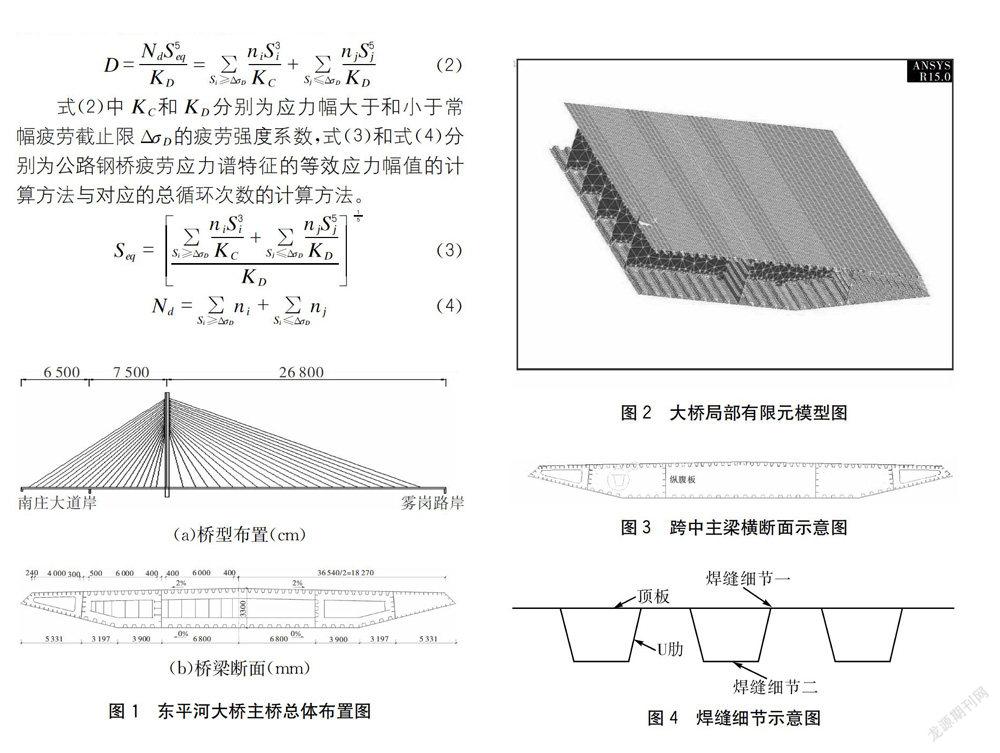
本文選取疲勞強度曲線時,參考的是歐洲EuroCode規范。由于疲勞損傷可以用等價原則進行處理,因此,可以用常幅應力循環來等效代替變幅應力循環,該常幅應力循環用Seq來表示。就公路鋼橋的疲勞問題來說,低于應力截止限△σL的應力循環多于高于應力截止限△σL的應力循環,即在疲勞應力譜中,低應力循環占主要部分。因此計算變幅荷載作用下細節的疲勞損傷的公式可以改寫為:
2工程背景
東平河大橋位于佛山市,為獨塔雙索面鋼一混凝土混合梁斜拉橋,其中墩、塔和梁為固結體系,橋梁全長約408m,橋跨布置為64m+76m+268m,邊中跨比為0.522;橋面以上塔高134.2m,塔高與主跨比約為1/2,邊跨距主塔中心線75m處設一個輔助墩;主橋橫橋向設雙向2%橫坡,橋面系寬36.5m,橋面布置為雙向六車道。東平河大橋整體布置如圖1所示。
3有限元建模及關鍵點應力響應面求解
為了實現荷載與應力效應之間的轉化,計算車輛荷載作用下焊接點的應力效應基于ANSYS有限元軟件平臺,采用Shell63殼單元建立正交異性鋼箱梁結構的有限元局部模型。結合正交異性橋面板局部荷載疲勞損傷特點,為了減少計算量,選用主跨跨中長度為18m的梁段,對其建立一半鋼箱梁有限元模型,作為本章研究的計算對象,并對局部有限元模型的邊界點的6個自由度進行限制。主梁的局部有限元模型與正交異性橋面板截面的橫斷面圖如圖2所示,選用的相應位置如圖3所示。其中焊縫細節一為頂板一U型肋焊縫,焊縫細節二為U型肋對接焊縫,對應的焊縫細節編號分別為50和71,焊縫細節詳細位置如圖4所示。
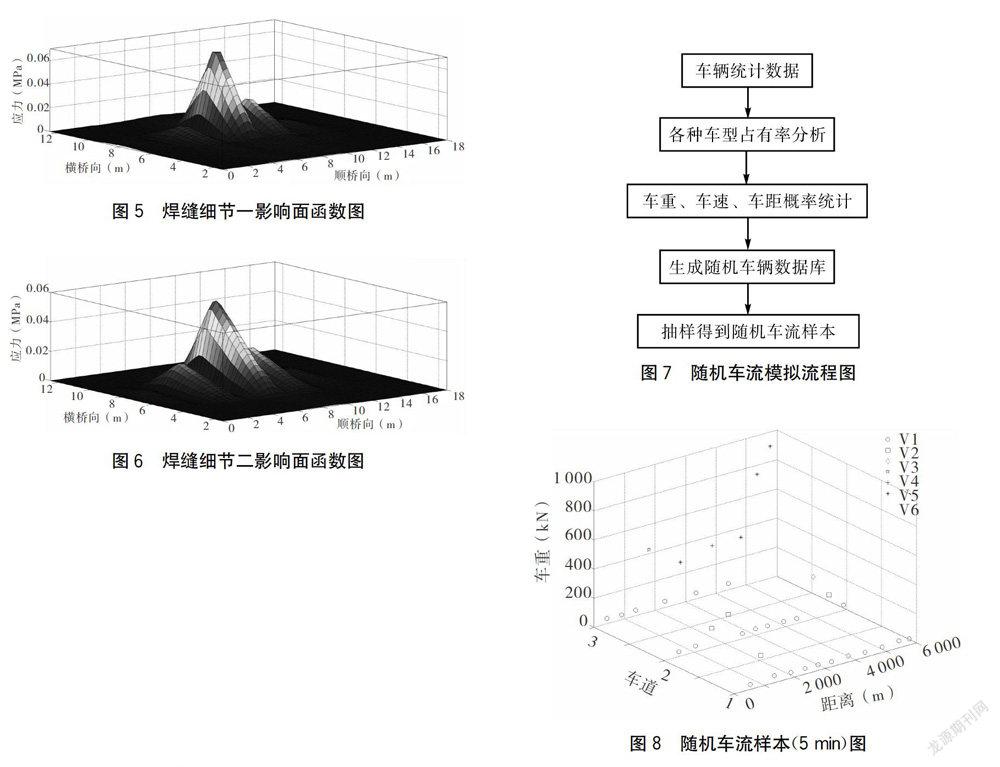
確定關鍵點之后,沿主梁橫斷面方向選擇三個行車道邊緣,分別沿橋縱方向91個節點位置采用單位移動豎向力(1kN)依次進行加載,得到6個斷面的各關鍵點疲勞參考應力的影響線豎標值,在此基礎上利用MATLAB的數據擬合工具箱Curve Fitting TooIbox對該6條影響線進行線性插值擬合得到曲面,并將擬合得到的結果保存為可調用的函數形式。焊縫細節一與細節二的應力影響面函數如圖5和圖6所示。
從圖可以看出,應力影響線的長度較短,主要集中在相鄰的兩橫隔板之間,車輛荷載作用下橋面板的應力響應表現為極強的局部效應,由此驗證了建立局部模型來分析橋面板焊縫細節疲勞性能的合理性。
4鋼箱梁細節疲勞壽命評估
4.1車輛相關參數統計分析
由于東平河大橋還未開始通車,本文重點研究的是隨機車流作用下橋面板的疲勞性能,因此,本文進行隨機車流模擬時采用的車型占有率、車輛質量、車間距等概率統計參數參考相關文獻中給出的參數,車速假設勻速。采用的日平均交通量為9800輛,分為六種車型,兩軸小可客車劃分為第一種車型,兩軸卡車與大客車歸為第二種車型,三軸、四軸、五軸和六軸貨車依次為第三種、第四種、第五種和第六種車型,六種車型占比分別為0.58、0.11、0.03、0.04、0.06、0.18。由于本文建立的是局部模型,只需要考慮一個行車方向上的各車型在三個車道上的分布情況。車距通常情況下服從Weibull分布,其分布參數七為300,λ為10。
4.2隨機車流樣本生成
基于上述車型、車道、車距、軸重這幾個相關車輛參數的分布類型與概率分布特性,在MATLAB平臺,再按照各自對應的概率分布進行抽樣得出隨機車輛樣本,連續抽樣就可以得到在時域上的隨機車流樣本。在時域內生成隨機車流的步驟如圖7所示,圖8為時長5min的隨機車流樣本。
從上述圖示內容可比較明顯地看出車輛的車型、車道、車重以及車距在橋面上隨時間的變化,在時長為5min的通行時間內,通過車輛的數量在45輛左右。第六種車型在車型比例中占比較高且車重最大,因此,在鋼橋面板的疲勞問題中,第六種車型應該引起重視。
4.3疲勞應力統計分析
基于擬合得到的標準梁段有限元模型的應力影響面函數與隨機車流樣本,可獲取應力時程。本文生成了兩個焊接細節在隨機車流作用下的應力時程,每個細節的應力時程長度為5min,樣本個數共計3萬個。本文中由于標準梁段的應力影響面沿橋面行車方向的長度較短,當車輛的車輪位置超出該應力影響面范圍時在影響面函數中數值記為零,且在標準梁段范圍內各細節主要受拉力作用。
從圖9(a)中可以發現,在時長為5min的隨機車流作用下,細節一的應力變化范圍大于細節二,其中細節一的應力范圍基本在20MPa之內,細節二則一般<15MPa,總的來說,在同一時刻細節一的應力響應大于細節二,但兩個細節的應力幅值均未超過常幅疲勞應力極限,可見,這兩個細節的應力具有幅值低、頻率高的特點。本文為了更加直觀地研究隨機車流作用下焊縫細節的疲勞損傷情況,對每一輛車的軸重進行了模擬,從圖9(b)可知,應力響應較大時出現兩個明顯峰值,這主要是由多軸貨車產生,多軸貨車前后軸距較長,且通過橋梁某一截面用時比兩軸車長,可形成多個應力峰值。
為了進一步分析各焊縫細節應力幅值與循環次數的變化情況,采用雨流計數方法對應力時程進行處理得到應力幅值與相應的循環次數。
從圖10中可以看出,在兩種構造細節中,低應力幅值的循環次數占絕大多數,高應力幅值的循環次數較少,但是低應力幅值產生的疲勞損傷非常有限,而高應力幅值產生的疲勞損傷占據主要部分,遠大于低應力幅值所產生的。
4.4疲勞壽命評估
疲勞損傷一般按一天的時長來計算,由于本文采用的是時長為5min的應力時程樣本,因此應將5min的循環次數換算為1d對應的循環次數,來計算1d大概的疲勞損傷,1d的循環次數計算公式如式(5)所示。焊接細節一與焊接細節二計算累積疲勞損傷的等效應力與循環次數如表1所示。
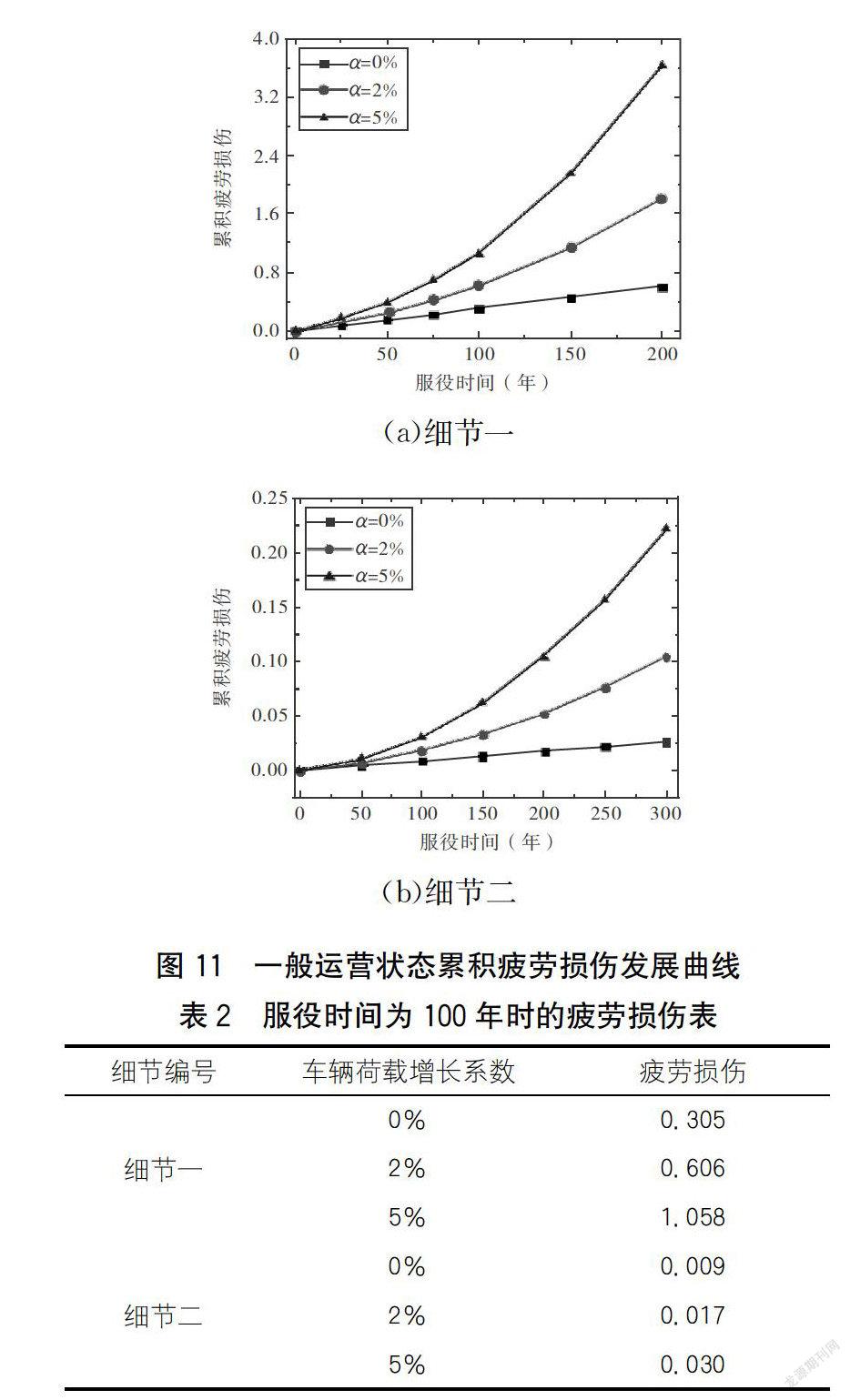
不考慮車輛荷載增長系數與考慮車輛荷載增長系數為2%和5%時,各焊縫細節不同年限對應的疲勞損傷如下頁圖11所示。
從圖11中可以看出,不考慮交通量增長的情況時(車輛荷載增長系數為0%),累積疲勞損傷隨著服役年限的增長呈線性增長的趨勢,而當考慮交通量增長系數時(車輛荷載增長系數為2%或5%),隨著服役年限的增長,累積疲勞損傷發展曲線呈非線性增長模式,并且隨交通量增長系數的增加,累積疲勞損傷增長的速度越快。對比細節一與細節二可知,細節一達到累積疲勞損傷極限的服役年限比細節二的要短。表2為當服役時間為100年時細節一與細節二疲勞損傷的對比情況,從表中可知,當達到設計基準年限時,細節一的疲勞累積損傷將大于細節二的,因此細節一的安全問題更需引起重視,應定期安排檢查與制定維修加固方案。
5結語
本文借助ANSYS有限元軟件建立了東平河大橋跨中主梁標準節段的殼單元有限元模型,并運用MATLAB生成了隨機車流作用下的焊接細節的應力時程,對橋面板U型肋兩種焊縫細節進行了疲勞壽命評估。結果表明:
(1)在實測車流數據的基礎上建立了隨機車流模型,基于S-N曲線和線性累積損傷準則,給出了考慮運營狀態和交通量增長的鋼箱主梁標準節段頂板U型肋的疲勞可靠度研究方法。
(2)對比頂板-U型肋焊縫與U型肋對接焊縫,在各種運營狀態下,頂板-U型肋焊縫達到累積疲勞損傷極限的服役年限比U型肋對接焊縫的要短。因此頂板-U型肋焊縫的安全問題更應該引起重視,定期安排檢查與制定維修加固方案。
(3)結合正交異性橋面板局部荷載疲勞損傷特點,為了減少計算量,可采用主跨跨中長度為18m的梁段,且僅建立其一半鋼箱梁有限元模型來作為疲勞壽命評估的研究對象。

