淺析設備厚度對風誘導共振的影響

張慶超

(中石化廣州工程有限公司,廣東 廣州 510000)

1 共振

共振[1](resonance)是指一物理系統在特定頻率下，比其他頻率以更大的振幅做振動的情形；這些特定頻率稱之為共振頻率。在共振頻率下，因為系統儲存了動能，很小的周期振動便可產生很大的振動。自然界中有很多地方有共振的現象，人類也在其技術中利用或者試圖避免共振現象。

機械共振是指機械系統所受激勵的頻率與該系統的某階固有頻率相近時，系統振幅顯著增大的現象。共振時，激勵輸入機械系統的能量最大，系統出現明顯的振型稱為位移共振。此外還有在不同頻率下發生的速度共振和加速度共振。

在機械共振中，常見的激勵有直接作用的交變力、支撐或地基的振動與旋轉件的不平衡慣性力等。共振時的激勵頻率稱為共振頻率，近似等于機械系統的固有頻率。

在一般情況下共振是有害的，會引起機械和結構很大的變形和動應力，甚至造成破壞性事故。防共振措施有：改進機械的結構或改變激勵，使機械的固有頻率避開激勵頻率；采用減振裝置；機械啟動或停車過程中快速通過共振區。另一方面，共振狀態包含有機械系統的固有頻率、最大響應、阻尼和振型等信息。在振動測試中常人為的再現共振狀態，進行機械試驗和動態分析。此外，利用共振原理的振動機械，可用較小的功率完成某些工藝工程，如共振篩等。

2 石化設備的風誘導共振

早在20世紀的初期，就出現一些鋼制圓筒形的煙囪在較低的風速作用下，以較高的頻率沿著與風力的垂直方向(橫向)產生振動，并導致結構破壞的事故。這種現象引起了人們的廣泛注意，并開始對這種橫向振動進行研究。安裝于石化的化工設備，如塔設備等，在風力的作用下，將產生兩個方向的振動。一種是順風向的振動，即振動的方向沿著風的方向；另一種是橫向振動，即振動方向沿著風垂直的方向，又稱橫向振動或風的誘導振動。風誘導振動比較復雜,國內外也有文獻對其研究進行了報道[2-4]。

2.1 風誘導共振的流體力學原理

當風以一定的速度繞流圓柱形的塔設備時，塔設備周圍的風速是變化的。由于風壓在塔設備周圍的變化，氣流在塔體背風面產生了漩渦，這樣的漩渦稱為卡曼漩渦[5](Karman Vertex)。

產生的漩渦特性與流體的雷諾數有關。當風吹過塔體時，如雷諾數Re<5，則塔體背風面的流線是封閉的，且塔體上、下的流線是對稱的，邊界層未發現分離現象；當5≤Re<40時，塔體背風面出現一對穩定的漩渦；當40≤Re<150時，在塔體背風面的一側先形成一個漩渦，在它從塔體表面脫落而向下游移動時，塔體背面另一側的對稱位置處形成一個旋轉方向相反的漩渦。在這個漩渦脫落時，在塔體背風面的原先的一側又形成一個新的漩渦，這些漩渦在尾流中有規律的交錯排列成兩行，如圖1所示，此現象工程上稱為卡曼渦街[5](Karman Street)。

圖1 卡曼渦街

當300≤Re<3×105范圍內，漩渦以一定的頻率周期性的脫落，該范圍稱為亞臨界區。當3×105≤Re<3×106范圍內，稱為過渡期。這時，尾流變窄，無規律且都變成紊流，無渦街出現。當Re>3×106范圍，稱超臨界區，卡曼渦街重新出現。在出現卡曼渦街時，由于塔體兩側漩渦的交替產生和脫落，在塔體兩側的流體阻力是不相同的，并呈現周期性的變化。在阻力大的一側，即漩渦形成并長大的一側繞流較差，流速下降，靜壓力較高；而阻力小的一側，即漩渦脫落的一側，繞流改善，速度較快，靜壓力較低，因而，阻力較大(靜壓力高)的一側產生一垂直于風向的推力。當一側漩渦脫落后，另一側又產生漩渦。因此在另一側產生垂直于風向，與上述方向相反的推力，從而使塔設備在沿風向的垂直方向產生振動，稱之為風誘導共振，也稱橫風共振。顯然其振動頻率就等于漩渦形成或脫落的頻率。

2.2 塔設備風誘導共振的激振頻率

在塔的一側，卡曼漩渦是以一定的頻率產生并從圓柱體塔體表面脫落的，該頻率即為塔一側橫向力FL作用的頻率或塔體的激振頻率。由研究表明，對于單個圓柱體，其漩渦脫落的頻率與圓柱體的直徑及風速有關，并可寫成下式表示。

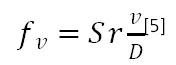
式中：v——風速，m/s;

Sr——斯特勞哈爾數，其值與雷諾數Re大小有關，具體相關性可查相關文獻；

D——塔體的外徑，如塔體有保溫層，則為保溫層外表面的直徑，m。

2.3 臨界風速

作用在塔體上的橫向力FL(也稱升力)是交變的，因為升力的頻率與漩渦脫落的頻率相同，所以當漩渦脫落的頻率與塔的任一振型的固有頻率一致時，塔體就會產生共振。塔體產生共振時的風速稱為臨界風速，若采用Sr=0.2，則由公式：

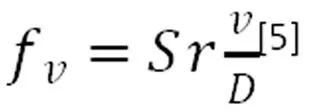
可求得臨界風速。

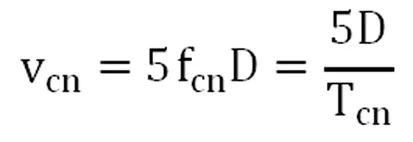
式中：vcn——塔在第n階振型下共振時的臨界風速，m/s；

fcn——塔在第n階振型時的固有頻率，1/s;

Tcn——塔在第n階振型時的固有周期，s;

D——塔的外直徑，m。

3 塔體厚度對共振的影響

如果塔體產生共振，輕則使塔體產生嚴重彎曲、傾斜，塔板效率下降，影響塔體的正常操作，重則使塔體嚴重破壞，造成事故。因此在塔的設計階段就應采取措施以防止共振的發生。

3.1 塔體厚度對臨界風速的影響

降低塔高，增大直徑，可降低塔的高徑比，從而增大塔的固有頻率或提高臨界風速，但這必須在工藝條件許可的情況下進行。而在實際的設計工作中，往往通過調整塔體厚度來緩解塔體的受力強度。本文針對塔體厚度對風誘導共振的影響，做了較為詳細的研究。現在通過一個設計案例，來討論塔體的厚度變化對風誘導共振的影響。

現在通過某項目脫丁烷塔案例，來討論通過調整塔體的厚度對風誘導共振的影響。相關設計參數如下：設計溫度：175℃；設計壓力：0.38MPa；直徑：2000mm；切線長：31700mm；裙座高度：8200mm；基本風壓 ：750；場地土類別 Ⅲ 類； 地面粗糙度 A 。根據設計需要，在塔體其他設計條件都不變的前提下，塔體的厚度分別選定為δ1=16，δ2=18，δ3=20，具體參數分別見表1，表2，表3不同厚度的同標高圓筒彎矩計算結果，分別顯示在對應的表格中。

表1 筒體厚度δ1=16時的設計參數和風載荷數據

表1為塔殼體厚度δ1=16時，圓筒風彎矩的計算數據。從數據可以看出，圓筒發生了一階和二階共振，且共振組合風彎矩明顯大于順風風彎矩。顯然，在設計參數下，筒體將可能發生劇烈的風誘導共振，塔設備也因此面臨很大的安全風險。

表2 筒體厚度δ2=18時的設計參數和風載荷數據

然而從表2中可以看出，塔殼體厚度δ2=18時，從圓筒風彎矩數據可以看出，筒體僅發生了一階共振，且共振組合風彎矩下降明顯，即此條件下，共振對塔體的安全影響較小。對比表1和表2的彎矩數據，發現兩者在共振時的一階振型的順風向風彎矩和橫風向風彎矩較為接近，而兩臺設備的受力差異主要源于二階共振的發生。因此可以看出，一階以上的高階共振對設備的受力影響顯著。

表3 筒體厚度δ3=20時的設計參數和風載荷數據

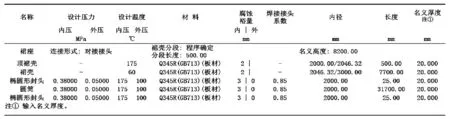
表3為塔殼體厚度δ3=20時，圓筒風彎矩的計算數據。通過對比數據，發現此厚度下的筒體也能避開二階振型共振的發生，所發生的一階振型所引起的共振風彎矩遠小于順風彎矩的影響。

表4 不同筒體厚度下的風載荷數據

為了更明確的觀察筒體厚度的變化對塔體受力的影響，現將不同厚度下的圓筒風彎矩匯總于表4。在表4中看到筒體厚度的變化對順風下的風彎矩并沒有明顯的影響，且一階振型下的共振風彎矩也較為接近，但呈現出有規律的遞增趨勢，而二階共振風彎矩有顯著的改變。綜上所述可以看出，共振振型越高，共振引起的風彎矩對塔體影響越大；同時也看出，隨著塔體厚度的增加，共振振型由二階共振減弱為一階共振。

由NB/T47041-2014標準中，塔式容器高振型計算模型可知，設備出現風誘導共振需滿足結構頂部風速VH>臨界風速Vcr。因此，接下來繼續考察筒體厚度與臨界風速的相關性。表5、表6、表7分別列出了塔體厚度δ1=16，δ2=18，δ3=20下，塔體的共振臨界風速。

表5 筒體厚度δ1=16時風誘導共振臨界風速數據

表6 筒體厚度δ2=18時風誘導共振臨界風速數據

表7 筒體厚度δ3=20時風誘導共振臨界風速數據

由表5、表6、表7可以看出，由于三臺設備的直徑和高度都相同，所以塔頂風速相同；而隨著筒體厚度的增加，看到一階，二階臨界風速都有明顯的遞增趨勢。由于三個塔體一階臨界風速都遠小于塔頂風速，故三個厚度下的塔體都發生了一階共振；同時可以看出，三個厚度下的塔體二階臨界風速也隨著厚度的增加而增加，并且當δ2=18時，二階臨界風速已經大于設備頂部風速，故當δ2=18時，設備已不發生二階共振。由此看來筒體厚度對風誘導共振確實有正的相關性，接下來本文將從數學模型中找出兩者的定量關系。

3.2 塔體厚度與臨界風速數學關系的推導

由于NB/T47041-2014中，僅僅給出里臨界風速和塔體自振周期的數學關系，并沒有明確給出塔體厚度和臨界風速直接的相關性，又因非等徑塔器的自振周期算式較為復雜，本文將模型簡化為：單種材質，等內徑，無外保溫，無外部附件的圓柱形塔體模型。現推導如下：

由臨界風速的計算公式：

(1)

式中：D——塔的外直徑；

Tcn——塔在第n階振型的固定周期；不等壁厚塔器第一振型的自振周期為：

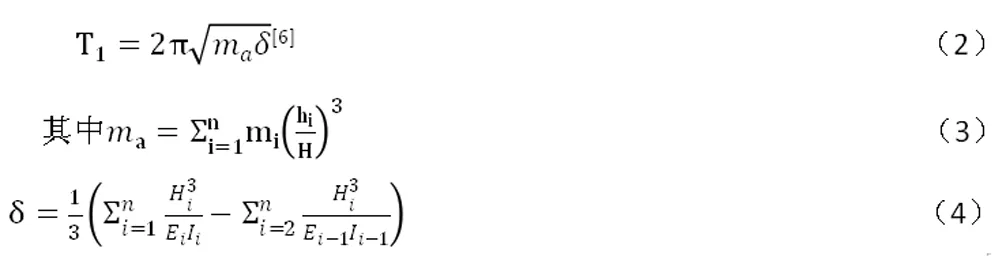
式中：Hi——第i段塔節底部截面到塔頂的距離，m;

Ei——第i段塔節材料在設計溫度下的彈性模量，Pa;

Ii——第i段塔節形心軸的慣性矩，對于圓柱形筒節；

δ——頂端作用單位力時所產生的位移，m/N;

ma——筒體總質量，kg;

hi——第i段筒節的高度，m;

Di——第i段圓筒的外徑，m;

Do——第i段圓筒的內徑，m。

ρi——第i段筒節的密度，kg/m3,則有

D平均——各筒節的加權平均外徑，m；

由于一般工程中Di/D0,可認為:

將公式(5)做同樣的相似替代可得

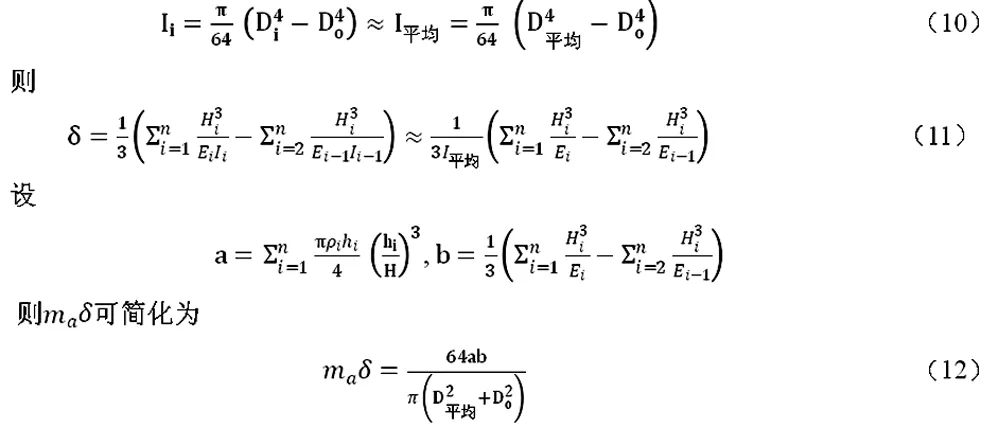
將式(12)代入式(2)可得

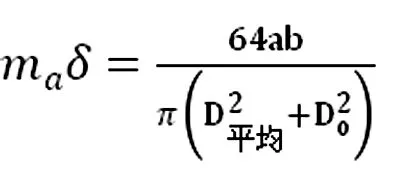
(13)

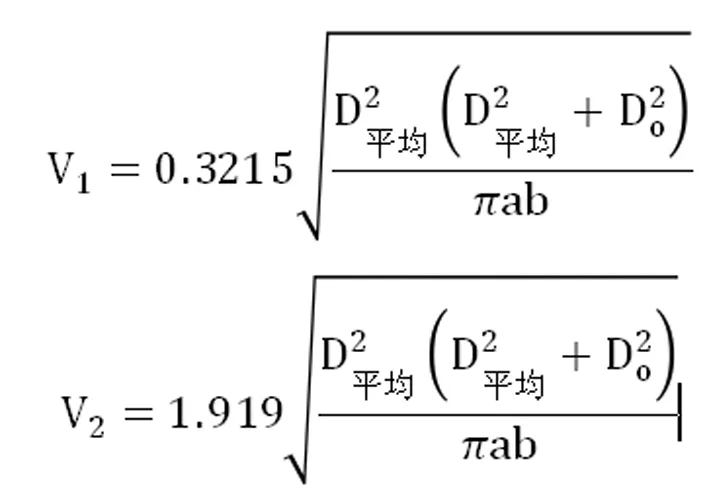
將式(13)代入式(1)，得一階振型的臨界風速的計算公式

(14)

其中:a,b——與塔體筒節i長度相關的量。在本文中僅討論厚度與臨界風速之間的關系，故ab值在此可以看做是與厚度無關的常數。

由推導公式可以看出，一階臨界風速隨著圓筒壁厚的增加而變大，并呈現出嚴格的數學相關性；NB/T47041-2014中，將直徑、厚度相等的塔式容器的第二振型近似的取T2=T1/6。因此可得二階臨界風速V2，

(15)

現將表5、6、7中關于臨界風速的數據匯總于表8。

表8 不同筒體厚度下的風速數據

由表8可以看出，隨著塔體厚度的增加第一臨界風速和第二臨界風速都遞增，且二階臨界風速的增加是一階臨界風速的6倍，這與NB/T47041-2014中T2=T1/6的近似保持一致；同時，發現設備厚度的增加，臨界風速的增加并非線性增加，而是隨著厚度的增大，臨界風速增加減弱，這與所推導公式所具有的開平方形式保持一致。因此，得出結論：對于長徑比>15的高聳設備來說，增加筒體的厚度，可以提高設備的抗震能力；并且本文給出了塔體厚度和臨界風速的數學等式。這對石化設計工作具有重要的指導作用。

4 結論

本文主要討論了在化工設備設計工作中，長徑比>15的高聳塔器在高風速下發生風誘導共振的相關問題。現將本文的研究結論總結如下：

(1)通過分析設計數據，發現筒體厚度的變化對塔體發生風誘導共振有較為明顯的影響，選擇合適的塔器厚度將能明顯改善塔體在高風速下的受力情況。

(2)通過已知的數學模型，推導出筒體厚度與一階，二階共振臨界風速的數學關系式，

(3)得出結論：對于長徑比>15的高聳設備來說，增加筒體的厚度，可以提高設備的抗震能力。