Mathematica在大學數學教學中的應用

蔡浩江 房敏 王婧嘉

【摘要】隨著現代信息技術以及計算機輔助教學的蓬勃發展，最新的信息技術已經在高等院校的日常教學中越來越普及.在大學數學的教學領域中，信息技術的應用，可以使艱深、復雜的數學理論和公式變得簡單直觀.將Mathematica這款非常實用的數學軟件與傳統教學相結合，構建符合學生認知規律的教學模式是提高大學數學教學質量的有效方法.實踐證明這種教學模式的建立對培養學生的數學思維，激發學生的學習主動性，提高教學效果有著非常重要的作用.

【關鍵詞】計算機輔助教學;數學軟件;Mathematica

一、目的與意義

高校的數學教學中，傳統的教學方法強調數學理論的連續與嚴謹，采用以教師為主導的灌輸式的數學教學模式，使原本就比較抽象難懂的數學定義與概念變得難上加難.

信息時代的到來，移動終端的使用，使傳統教學模式受到了強烈沖擊.當前，學生獲取知識的渠道變得更為豐富，各種MOOC、微課學習視頻及其他豐富的網絡教學資源都為學生的課外學習提供了條件.

但是與傳統教學相似，各種網絡教學資源仍注重于學生掌握嚴謹的數學理論和計算能力，忽略了理論知識的推導以及創新思維的培養，淡化了理論推導過程中的猜想、觀察、實驗、歸納、類比、抽象等環節，忽視了學生的主體地位，弱化了學生自主探索的學習過程，不利于培養學生的應用與創新能力.對大多數學生而言，這些資源的利用雖然能夠在一定程度上提高他們的學習效率，但仍然無法將所學的數學知識應用于其他課程及解決實際問題，學生的邏輯思維能力、創新與應用能力并沒有顯著提高.

教學實踐證明，數學軟件與傳統課堂教學的有機結合，是提高學生創新思維和應用能力的一條行之有效的途徑.一方面，數學軟件可以使用圖像展現數學深奧的理論，可以加強學生對抽象知識的理解.另一方面，為了貫徹實施素質教育，教師還可以設計數學課程的實驗教學環節：提出典型實際問題，引發學生思考，培養學生的數學思維;在教師的啟發下分析問題、探索問題，從而提高學生的創新精神和實踐能力;利用數學軟件進行數學實驗，使學生對教學內容有了直觀認識，從而提升學習興趣，提高研究能力.學生在使用數學軟件解決問題的過程中找到了理論與實際的結合點，體驗到了“學”和“用”的和諧統一，獲得了學習帶來的成就感，學習興趣和動力會得到長效的保持.

二、計算機輔助教學的可行性

教學硬件的改善為軟件的使用提供了保障條件.Matlab、Mathematica、Maple并稱為三大數學軟件.Matlab是Math Works公司出品的數學軟件，用于算法開發、數據分析以及數值計算;Mathematica是由美國的Wolfram Research公司開發的數學軟件，其在圖形、數值、代數等方面應用廣泛;Maple是由加拿大Waterloo大學開發的科學計算軟件，擁有優秀的符號計算和數值計算能力.它們各有所長，但就高校計算機輔助教學及實驗教學而言，Mathematica更具優勢，原因有：第一，Mathematica有與數學教材完全相同的基本數學符號輸入界面，見圖1，不需要太多的課堂時間講解，學生即可上手使用;第二，自定義函數的寫法，各類函數的輸入和輸出，更接近語言的表達順序，簡單易懂;第三，繪制的三維圖形可以方便地調整觀察視角，有利于學生對空間圖形的直觀認識;第四，符號運算方便、簡潔，容易掌握.

因此，將Mathematica數學軟件引入數學教學中具有很好的可行性.通過它，可以將復雜抽象的計算問題按照人們習慣的書寫格式輸入和輸出，學生容易掌握，還可將復雜的函數關系用圖形的形式展現出來，便于將抽象的問題具體化、可視化.

本文將以Mathematica的幾個輔助實驗為例說明與傳統教學相結合的教學模式對提高大學數學教學效果的積極作用.

三、Mathematica軟件在輔助教學的應用

（一）在觀察數列變化趨勢中的使用

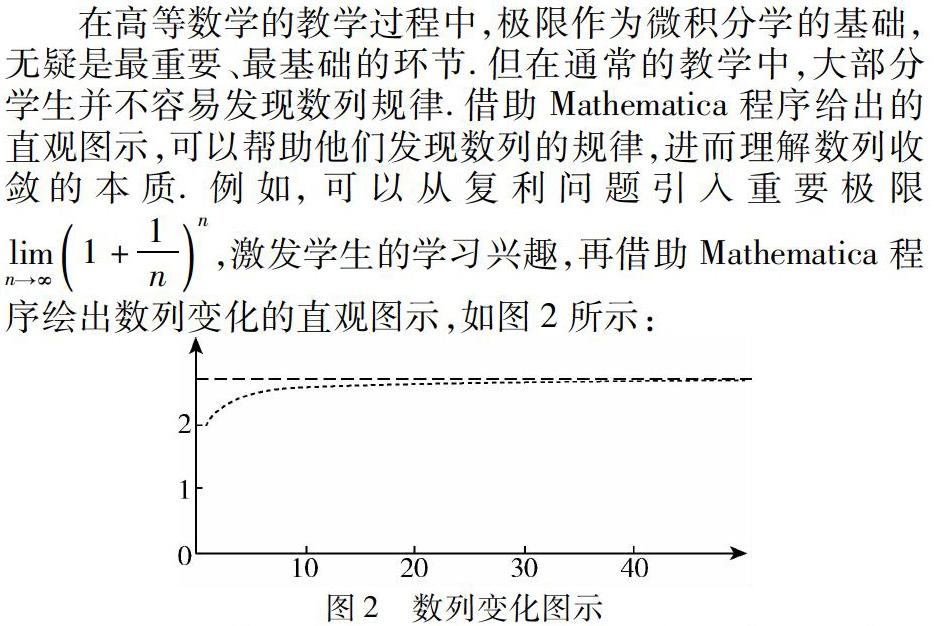
在高等數學的教學過程中，極限作為微積分學的基礎，無疑是最重要、最基礎的環節.但在通常的教學中，大部分學生并不容易發現數列規律.借助Mathematica程序給出的直觀圖示，可以幫助他們發現數列的規律，進而理解數列收斂的本質.例如，可以從復利問題引入重要極限 limn→∞1+1nn，激發學生的學習興趣，再借助Mathematica程序繪出數列變化的直觀圖示，如圖2所示：

學生從圖像中觀察到了數列變化的特點，直觀的感受使學生對公式首先有了感性認識，以此為基礎，再利用二項展開式進行公式的推導和理論證明，從而使學生上升到理性認識.此過程遵循了猜想、觀察、實驗、歸納、類比、抽象的環節，重在思維方式的啟發與培養，引導學生獨立思考并提升了學生學習的積極性和主動性.

（二）在函數繪圖中的使用

在傳統的高數課堂教學中，由于缺乏對復雜函數圖像的描繪等教學環節，對很多學生而言，曲線的直角坐標方程、極坐標方程及參數方程3種表達方式之間相互轉化;不同坐標系下的三重積分的計算;線、面積的計算;隱函數的概念等知識點一直以來是都是難點問題.“數”與“形”之間不能完美的結合，使得部分學生缺乏直觀認知，造成概念混淆，無法深入理解相關知識.但是在計算機輔助教學中，我們就可以借助Mathematica中的繪圖軟件，在教學過程中繪制復雜函數的圖像，“數”與“形”的有機結合，可以使抽象函數具體化，加深學生對函數以及相關知識的理解.使用Plot、PolarPlot、ParametricPlot函數繪制一元函數、極坐標函數、參數方程表示的二維圖形，使用Plot3D、RevolutionPlot3D、SphericalPlot3D、ParametricPlot3D函數繪制二元函數、柱坐標函數、球坐標函數、參數方程表示的三維圖形，使用ContourPlot繪制隱函數圖形.還可以通過CoordinateTransform函數實現直角坐標Cartesian，極坐標Polar，柱坐標Cylindrical，球坐標Spherical之間的相互轉換.如圖3繪制了極坐標方程ρ=cos2θ表示的四葉玫瑰線和方程x3+y3-3xy=0確定的函數曲線.

還可以通過Animate函數繪制動畫，演示擺線、旋轉曲面等圖形的形成過程，如圖4所示，幫助學生更好地理解所學內容并增強學生的學習興趣.

（三）在定積分和二重積分定義中的使用

積分在數學、物理、機械、電子、軍事等方面均有著廣泛應用，但積分的概念對大部分學生而言卻是難以理解的.在教學中，我們一般通過求曲邊梯形面積和曲頂柱體體積的問題引入，需要經過“分割、近似代替、求和、取極限”四個步驟進行.其中“取極限”這一環節，課堂教學僅通過語言描述表達，沒有相關的實驗環節，學生缺乏直觀的感性認知以及從具體到抽象的思維過程，無法深入、透徹地理解相關概念，難以獲得較好的教學效果.通過Mathematica繪制具體例子的圖示，如圖5所示，以圖形直觀的方式呈現，遠勝于教師的口頭講解，有助于學生加深印象并理解概念.

（四）在大數定律中的使用

大數定律是概率統計中的重要定理，揭示了n個相互獨立的隨機變量的算術平均值當n→∞時依概率收斂于其數學期望.為了幫助學生更好地理解大數定律，可以利用Mathematica給出直觀演示.例如，在講授辛欽大數定律時，利用Mathematica的Random和NormalDistribution函數，產生n個相互獨立且服從正態分布N（1，22）的隨機變量X1，X2，…，Xn，考查當隨機變量個數n逐漸增多時，它們的算術平均值的變化情況.圖6分別給出了當n=10，100，1 000，10 000四種情況下，重復試驗50次，n個隨機變量的算術平均值的分布情況.

從圖6可以明顯看出，當n=10時，10個相互獨立的隨機變量的算術平均值與μ=1有很大偏差，但隨著n越來越大，n個相互獨立的隨機變量的算術平均值越來越密集在μ=1這條直線附近.由此可見，傳統教學中復雜、艱深的數學定理，借助于數學軟件的幫助，以直觀易懂的圖形圖像展示給學生，使得復雜抽象的理論知識變得簡單、具體，讓學生印象深刻，從而取得較好的教學效果.

四、計算機輔助教學的優點

（一）有利于學生自主學習

數學課程的教學強調進行交互式教學以及以學生為中心的自主學習，在課前、課中和課后都以學生為主體、教師為主導.數學軟件輔助教學，使得作為主體的學生，對課程知識的獲取和掌握不再完全依賴于任課教師的課堂教學，可以利用更多的課外時間自主學習.

（二）有利于學習成績的提高

在運用計算機輔助的交互教學過程中，將Mathematica軟件引入到數學課堂，使抽象的概念、函數、公式變得直觀形象，學生在數學模型的動態展現中更加深刻地理解理論知識，提高課堂的教學效率，提升學生的學習興趣.學生在學習過程中遇到難題，也可以通過討論，查找資料，編寫程序等多種方式加以解決.

（三）有利于實踐能力的培養

在課程教學中，我們運用Mathematica軟件進行交互教學，讓學生通過自主學習的方式不僅掌握有關定理、公式，而且能夠熟練掌握一門數學軟件.既增強了學生的自學能力，還提高了學生的動手能力，也培養了學生的實踐應用能力.

五、結束語

在數學課程中運用Mathematica軟件進行輔助教學，充分利用數學軟件的計算和繪圖功能，加強了數學教學的簡便性和直觀性，使得“數”與“形”有機結合，“教”與“學”相得益彰，不僅有助于提高課堂教學效果，還有助于培養學生利用數學軟件探究問題的意識.學生在課后利用課外教學資源自主學習、表達和解決實際問題時，也可以方便地使用軟件輔助，既促進了學生學習成績的提高，也培養了學生理論聯系實際的能力.教學實踐證明，在數學教學中充分利用輔助軟件是一種比較科學有效的教學方法，能夠激發學生的學習興趣，活躍課堂氛圍，提高課堂教學效果.

【參考文獻】

[1]同濟大學數學系.高等數學（上冊）：第7版[M].北京：高等教育出版社，2014.

[2]同濟大學數學系.高等數學（下冊）：第7版[M].北京：高等教育出版社，2014.

[3]朱開永，王升瑞，李媛.概率論與數理統計[M].上海：同濟大學出版社，2013.

[4]Wolfram S.Mathematica全書[M].赫孝良，周倉義，譯.西安：西安交通大學出版社，2002.

[5]王紹恒，王藝靜.Mathematica軟件在大學數學課程教學中的應用[J].教育理論與實踐，2013（21）：39-40.

[6]劉雄偉.基于Mathematica的高等數學教學過程研究與實踐[J].大學教育，2016（2）：136-138.