變式例題 引導學生探究
季新兵
摘 要:新課程改革的不斷深化,對學生的評價也隨之發(fā)生了巨變。從注重評價學生知識的掌握到注重培評價學生能力的發(fā)展。《新課程標準》指出:教學中應當有意識有計劃的設計教學活動,引導學生體會數(shù)學之間的聯(lián)系,感受數(shù)學的整體性,不斷豐富解決問題的策略,提高解決問題的能力。
變式例題,是一個非常好的切入點。教師在平時的課堂教學中要讓學生多體驗數(shù)學的探究過程。教師可根據(jù)例題的特點,對例題由特殊到一般,或?qū)⒗}的條件與結(jié)論交換,或者改變例題條件,弱化條件等,引導學生作深入的探究,提高分析問題,解決問題的能力。
課堂實踐與體會
例題1:設sn是等比數(shù)列的{an}的前n項和,若s3,s9,s9成等差數(shù)列,證明a2,a8,a5成等差數(shù)列。
此題的證明比較簡單,學生大都可以獨立完成證明。將此題由特殊到一般進行變化,引導學生探究。
探究1 設sn是等比數(shù)列的{an}的前n項和,若sk,s3k,s2k(k∈N*,k≥2)成等差數(shù)列,證明ak-1,a3k-1,a2k-1成等差數(shù)列。
交換該例題的題設與結(jié)論,引導學生進一步探究
探究2 設sn是等比數(shù)列的{an}的前項和,其公比q≠1,若ak-1,a3k-1,a2k-1(k∈N*,k≥2)成等差數(shù)列,證明sk,s3k,s2k也成等差數(shù)列。
由上述兩題的證明,可引導學生進一步得出結(jié)論:
設sn是等比數(shù)列的{an}的前n項和,其公比q≠1,sk,s3k,s2k(k∈N*,k≥2)成等差數(shù)列的充要條件是ak-1,a3k-1,a2k-1成等差數(shù)列。
這一組例題的設計,先易后難,逐級而上。第一組題起點低,按課堂最低要求設計,適宜整體學生的學習水平的提升。隨著問題的一步步深入,內(nèi)容上由易變難,方法上由死變活。不斷激發(fā)學生的學習欲望,使得一部分高層次學生的知識和能力得到潛移默化的提高。
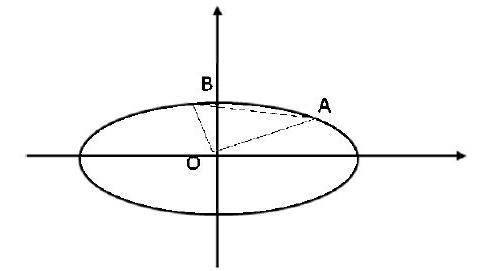
例題2、過橢圓x2/a2+y2/b2=1(a>b>0)的中心O作互相垂直的兩條弦,與橢圓交于點A、B。求證:1/|OA|2+1/|OB|2為定值。
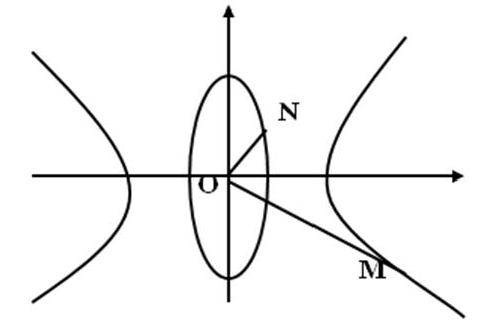
變式1:雙曲線C1:2x2-y2=1與橢圓C2:4x2+y2=1,點M、N分別為C1,C2上的動點,且OM⊥ON(O為原點)。求證:點O到直線MN的距離為定值。
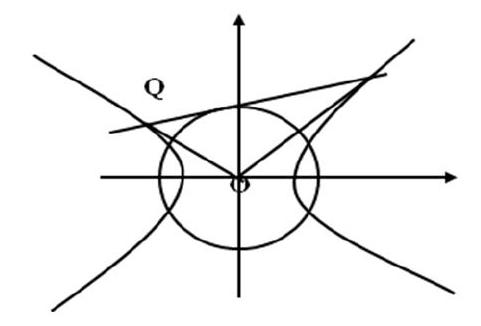
變式2、雙曲線2x2-y2=1,設斜率為k的直線l交雙曲線于P、Q兩點,若直線l與圓x2+y2=1相切,求證:∠POQ為定值。
通過例(2),學生掌握解題規(guī)律、方法,并把它運用到變式1變式2同一類題目的解決過程,使解題方法得到遷移,形成技能技巧。
例題3:已知拋物線y2=2px(p>0),O為坐標原點,過點(2p,0)作直線與拋物線交與A,B兩點,求證:OA⊥OB。
該題學生只要正確設直線方程,證明OA⊥OB即可。屬于基礎(chǔ)題。
探究1:已知拋物線y2=2px(p>0)過其頂點O做兩條弦OA,OB,交拋物線于A,B兩點,使得kOA·kOB=-1,試證明直線AB過定點。
探究2:若將點O改為過拋物線上任一點P(x0,y0),作兩條互相垂直的弦PA,PB,則直線AB是否過定點?
探究3:如果將條件改為過拋物線頂點,作兩條弦OA,OB,使得kOA·kOB=m,m為非零常數(shù),則直線AB是否過定點?
探究4:更一般化,將條件改為過拋物線上任一點P(,)作兩條弦PA,PB,使得kPA·kPB=m,m為非零常數(shù),則直線AB是否過定點。
探究1:過定點(2p,0)? ? ? ? ? 探究2:過定點(2p+x0,-y0)
探究3:過定點(-2p/m,0)? ? 探究4:過定點(-2p/m+x0,-y0)
這一組例題,既有聯(lián)系,又有區(qū)別。學生做完這一組習題后,引導學生反思一下,到底解題關(guān)鍵是什么,自己的障礙和困難在哪里。有哪些收獲。進一步引導學生觀察,比較揭示隱藏在這一組習題中的一般方法,推廣為同一類對象的普遍性質(zhì),揭示解題規(guī)律,提高分析、探索能力和創(chuàng)新能力。
變式例題,加大了課堂容量,提高了課堂效率,使各個層次的學生都有所提高。通過對例題進行多角度、多方面的變式探索研究,有意識的引導學生從“變”的現(xiàn)象中發(fā)現(xiàn)“不變”的本質(zhì),從“不變”的本質(zhì)中探索“變”的規(guī)律,不僅能加深學生對概念的理解,形成完整的知識結(jié)構(gòu),培養(yǎng)學生舉一反三,觸類旁通的變通能力,促進知識的遷移。還能提高學生學習數(shù)學的興趣,激活個人的智慧,鍛煉學生的思維能力和創(chuàng)造能力。
參考文獻:
[1]《一道例題的變式探究》 作者 黃傳峰? ?新課程研究教師教育2013年第4期.

