鐵路運營物資區域聯合儲備中心選址

田 源，楊 瑩，李伊松，施先亮

（1.北京交通大學 經濟管理學院，北京 100044；2.北京交通大學 法學院，北京 100044）

1 引言

區域聯合儲備是基于聯合儲備中心的各參與主體間權利、責任、風險共擔的庫存管理模式。依托參與主體間的地域及資源優勢，實施共性物資的聯合儲備，一方面通過減少重復儲備，有效降低庫存水平，節省倉儲費用；另一方面，通過資源整合，有助于促進整體庫存管理水平的提升。而區域儲備中心選址是聯合儲備管理中的重要戰略決策之一，合理的選址規劃不僅關系到資源統籌、效益最大化等目標的實現，也關系到供應的準時性問題。在鐵路物資管理的背景下，由于鐵路運營物資具有品類多、庫存大的特點，且各鐵路局之間存在地域差異及管理差異等問題，所以在其運營物資聯合儲備中心選址問題中進行合理的區域劃分及儲備中心選址至關重要，成功的選址規劃將會帶來資金、人力、土地等方面資源的節省，有效提升經濟效益。

2 文獻綜述

以下將從物資聯合儲備管理及儲備中心選址兩方面進行綜述。一方面，目前針對聯合儲備管理問題的研究較為豐富，且較多基于企業管理實踐的研究，如崔巍[1]在石化企業采購和儲備管理中引入了區域協同采購、區域聯合儲備及JIT的管理理念。張淼[2]研究指出聯合儲備庫存管理模式可以在保證安全生產的基礎上，優化庫存資源配置，減小庫存資金占有，提高資金周轉率。安莉[3]、陳謙，等[4]分別針對電網企業和核電廠的聯合儲備管理問題進行了研究，并用實例說明聯合儲備所帶來的好處。王科清，等[5]研究指出聯合儲備管理的優勢在于能夠提高突發事件下的電網事故應急處理效率，縮短恢復供電時間，減少停電損失，提高管理水平。另一方面，目前有關儲備中心、配送中心選址的研究已經較為成熟，而聚類思想在選址問題研究中也是一種比較常用的方法。其主要思路是基于相似度的思想將客戶點聚類成客戶群，從而劃分成多個配送區域問題。例如，秦固[6]、Liu[7]等人均是將客戶點進行聚類，從而將多配送中心選址問題簡化為若干個單配送中心選址問題。陳磊，等[8]、孔繼利等[9]則基于模糊聚類的思想構建指標體系，從而實現備選配送中心的劃分，然后將問題轉化為區域內配送中心選址問題。除去上述方法，k-means作為一種經典的聚類方法，也在選址問題研究中得到了廣泛應用。王信波，等[10]、L，等[11]和王云婷，等[12]均采用k-means聚類方法并結合其他選址方法研究配送中心的選址問題。

綜上所述，雖然目前針對儲備中心選址問題的研究較為豐富，但針對鐵路物資管理及聯合儲備中心選址的研究較少，所以本文為實現我國鐵路物資管理資源統籌共享的目標，針對區域聯合儲備中心選址問題，首先基于改進的k-means聚類算法對區域進行劃分，確定配送區域的范圍及成員組成，其次通過多目標選址模型在劃分完成的區域內選擇合適的組織單位負責聯合儲備的物資管理及存儲問題，實現儲備中心的選址。

3 基于k-means的聯合儲備區域劃分

3.1 改進K-means聚類算法

k-means算法是較經典且應用范圍比較廣泛的聚類分析方法，被廣泛的應用于配送網絡中的配送區域劃分分析中，其聚類的目標是盡可能的使各聚類中的末端點相互緊湊，并盡可能使各聚類間相互分開。其優點是可以高效的處理大數據集，且可以得到很好的聚類效果。但考慮到傳統k-means算法對初始聚類中心的選取比較敏感，中心選取不當會大大影響聚類結果，以及算法易受噪聲和孤立點影響的事實，鑒于此，本文將引入密度思想對傳統kmeans算法做如下改進。

3.1.1 引入密度指數。基于密度思想并引入密度指數來確定k個聚類中心，按照從大到小的順序排列，選取前k個數據點作為聚類中心。其中密度指數的確定方法如下：計算每個數據點Xi的密度(其中i代表數據點的個數，i=1，2，…，n)，R為該點鄰域半徑當i取某一數值，j=1,2，…，n，Pi代表Xi的密度指數，表達式如下：

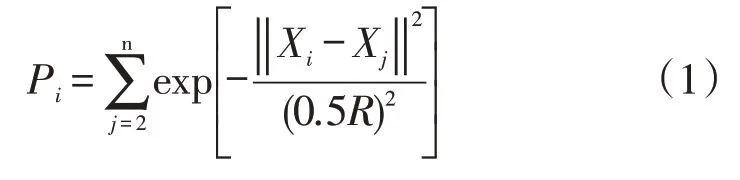
3.1.2 定義相似度。傳統算法中用兩點之間的空間距離來定義兩點相似度的方法，顯然在本文的應用背景下是不可取的，為了更科學的衡量鐵路局在物資管理方面的相似性及進行聯合儲備時距離的可行性，本文借鑒城市經濟引力模型，以聯合采購的物資采購額作為衡量鐵路局的經濟引力因子，交通運輸時間作為衡量物資調撥難易程度的距離因子。則重新定義的距離因子d(Xi-Xj)計算公式如下：

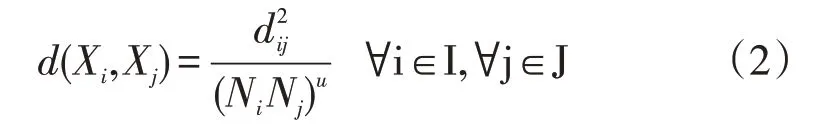
其中Ni,Nj分別代表鐵路局i和鐵路局j的聯合采購物資采購額，由于進行聯合儲備的前提是各鐵路局之間的物資需求量相當，且物資采購需求大的鐵路局說明其綜合實力更強，所以聯采物資總額是衡量鐵路局聯合儲備適應度的重要指標。dij為鐵路局i和鐵路局j的交通距離，本文以車輛在兩座城市之間行駛一趟的交通時間來衡量。u作為調節物流網絡劃分時受聯儲物資需求特性的影響程度。一般來說，u越大，則說明在區域物流網絡劃分時，各鐵路局的聯儲物資需求量的吸引力占主導地位，同時距離因素被一定程度弱化。反之u越小，則距離的影響程度更大，而u=0時，距離即為歐式距離。

3.1.3 確定聚類數目。由于k-means算法的聚類結果受k值的影響較大，所以為提高聚類結果精度，本文采用迭代的方法對k值進行選取。通過計算類別內的組內平方和的評估方法對k值進行篩選，計算公式如下：

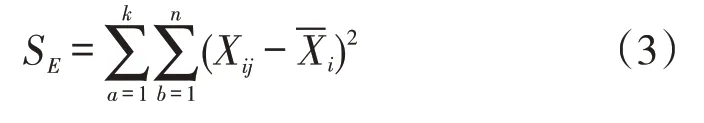
其中式（3）代表組內平方和，即樣本點與各自聚類中心的距離平方之和，值越小則代表總的聚類距離越小，聚類效果越好；反之值越大，聚類距離越大，聚類效果越差。用組內平方和的方法確定最佳聚類個數，以達到更好的聚類效果。

3.2 改進k-means算法計算步驟

改進的k-means算法的實現步驟如下：

（1）首先，對數據進行歸一化處理。

（2）按照式（1）計算密度指數并按從大到小排列。

（3）取前k個候選點作為聚類中心，按照式（2）計算當k取不同值時的相似度。

（4）計算種聚類結果的組內平方和，選取最優k值，確定最佳聚類方案。

4 區域內聯合儲備中心選址

4.1 問題分析

在進行鐵路物資聯合儲備區域劃分的基礎上，現需在各個聯合儲備區域內選擇一個或多個鐵路局進行聯合儲備物資的存儲及管理，所以需要對物資的儲備地點進行選擇。而由于鐵路物資需求特性，該選址問題具有以下特點：首先，聯合儲備中心的地理位置對物資供應的保障程度至關重要，且同時要盡量減少總的物資配送與調撥成本；其次，由于鐵路物資種類繁多，僅僅根據一類物資的最優方案來確定儲備中心位置顯然不合理，所以需要同時考慮多類物資；再者，由于聯儲物資通常具備價值高，體量大，所需存儲空間大，對存儲環境要求較高，需要認真選擇備選點。

4.2 選址原則

（2）適應性原則。鐵路物資聯合儲備中心的選址應與國家以及地方政府的經濟發展規劃、大政方針、經濟政策相適應，與物流資源分布和需求分布相適應，與當地經濟發展和社會發展相適應。

（3）協調性原則。鐵路物資聯合儲備中心選址應將鐵路倉儲網絡作為一個整體進行系統的考慮，使倉庫選址有利于其他資源的利用，共同產生更大的經濟效益。

（4）保證供應原則。儲備中心的最大儲備量應滿足其所服務半徑內所有需求點的需求，正常情況下，區域內供應原則是就近供應，但當面臨就近儲備中心無法滿足需求，或同時出現兩個需求點在同一儲備點服務半徑內需要供應，或發生特別重大事故等特殊情況時，就需要其他儲備中心的聯合供應以及時滿足需求，從而保證鐵路正常運營。

4.3 選址目標

（1）目標1-保障供應。考慮到鐵路行業對物資需求的特殊要求，在進行聯合儲備中心選址時不能以犧牲供應及時性為代價，所以聯儲中心需要在各需求點所期望的時間范圍內將物資送達。

（2）目標2-成本最小。鐵路物資聯合儲備的目的就是通過資源整合與共享，降低整體存儲規模，從而降低各鐵路局及鐵路物資管理總成本并提高資源利用率。

4.4 雙目標選址模型構建

在進行選址原則及目標分析的基礎上，聯合儲備模式下儲備中心選址模型簡述如下：

4.4.1 成本最小目標。聯合儲備中心選址的主要目的是減小物流成本，而運輸成本一方面在物流成本中占絕大比例，另一方面由分散儲備管理模式轉為聯合儲備主要對運輸成本的影響最大，所以除考慮存儲成本及訂貨成本外，運輸成本也作為成本因素的重要考量，總成本計算結果如下：

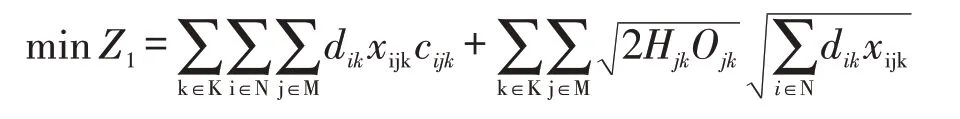
其中N：代表需求點集合，N={1，2，…，n}；M：代表儲備中心備選點集，M={1，2，…，m}；K：代表物資種類集合，K={1，2，…，k}；dik：代表需求點i對物資k的平均需求量(件/天)；cijk：代表第j個儲備中心向第i個需求點供應第k種物資的單位運輸成本(元/件)；Hjk：備選點j對物資k在單位時間內單位物資的存儲費用（元/件天）；Ojk：備選點j對物資k的訂貨費用（元），此費用為常量，在每次訂貨時發生，并與訂貨量無關；xijk為0-1變量，當第j個儲備中心向第i個需求點供應第k種物資時為1，否則為0。

4.4.2 時間滿意度最大目標。鐵路行業與一般的交通運輸企業不同，鐵路運營物資的供應中斷所帶來的風險不可估計，對于時間敏感度較大的物資來說，供應中斷輕則會影響列車的正常運行，重則會產生運行安全問題，所以鐵路行業的第一要務就是保證運營物資供應的及時性，由此看出鐵路運營物資是時間敏感度較高的物資。所以及時保量的供應是鐵路物資儲備中心選址所不可忽略的目標和原則。

六是實施技術引領方略，提高水資源的可用性。開源方面，積極發展海水淡化技術、雨水利用技術及替代性水源開發技術；再利用方面，提升污水處理技術、中水回用技術、生物技術水平；節流方面，加強節水設備研發、規范產業節水管理技術，應用節水評價技術；科技支撐體系方面，建立水沙監測與預測預報體系，完善水資源監控體系，建立水安全預警系統等。

因此需求點對于儲備中心物資供應的遲到要給予一定懲罰，需要結合懲罰函數的思想將時間延遲造成的成本損失定量表達，時間懲罰成本函數有很多表現形式，一般需要結合具體情況進行選取。

（1）時間滿意度函數選取。目前研究中常用的時間滿意度函數主要有以下5種。下面通過分析各類滿意度函數的適用條件(見表1)，從而找出適合本文研究背景的時間滿意度函數。

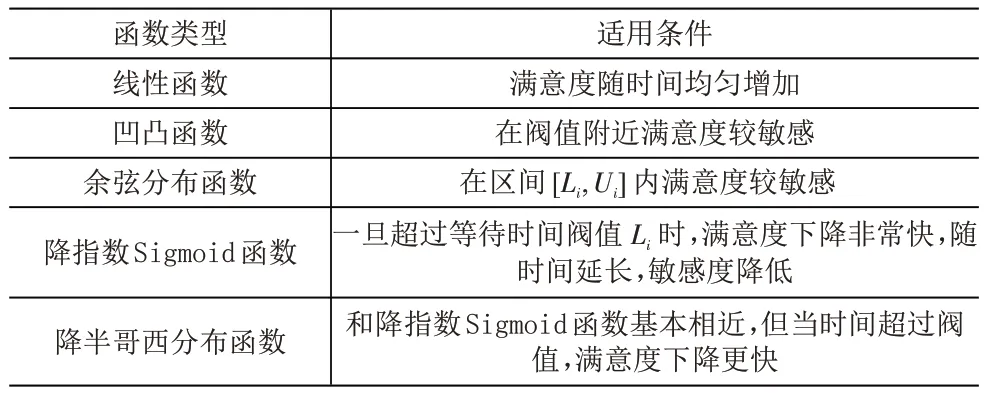
表1 時間滿意度類型及適用條件分析

（2）鐵路物資供應時間懲罰成本。由于鐵路運營物資對于供應及時性要求較高，一旦超過約定時間，短時期內滿意度將會迅速下降產生較高的懲罰成本，所以降半哥西分布時間滿意度函數最適合本文的研究背景，本文將采用此函數來構造時間懲罰成本函數，降半哥西分布時間滿意度函數圖像如圖1所示。

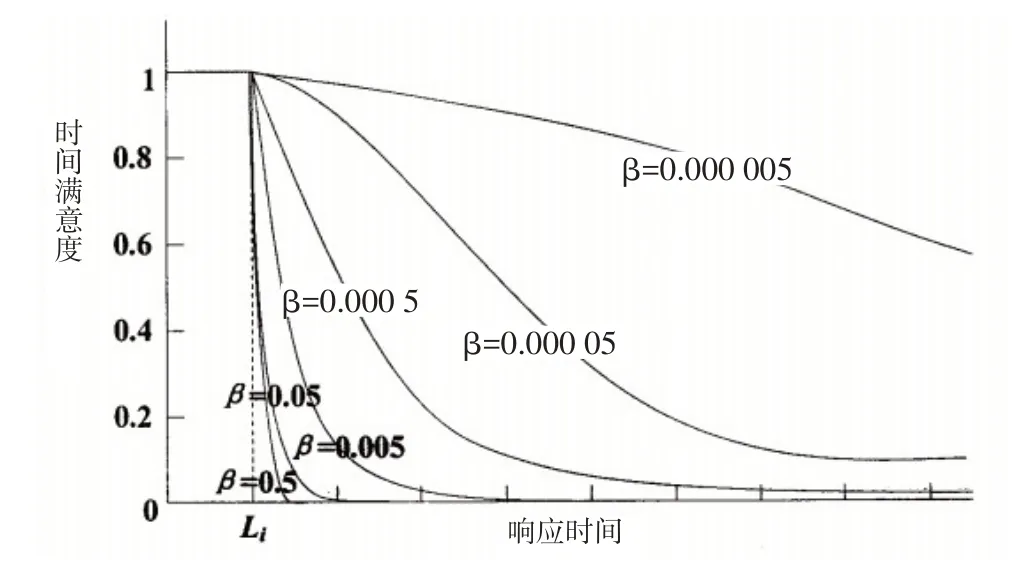
圖1 降半哥西分布時間滿意度函數圖像

可以看出時間滿意度函數中自變量和因變量呈反向變化，等待時間越長需求點的時間滿意度水平越低，而時間懲罰成本與等待時間成同向變化，即等待時間越長，供給點應該付出的懲罰成本越多。用時間滿意度水平的倒數來構造時間懲罰成本函數，通過降半哥西分布時間滿意度函數可得：

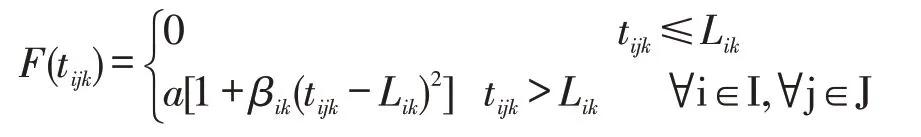
其中，F(tijk)：需求點i向供給點j供給物資k的時間懲罰成本；a：單位時間懲罰成本；βik：需求點i對物資k的時間敏感系數；tijk：需求點i接受供給點j提供物資k的最短等待時間；Lik：需求點i感到滿意度下降的臨界點，即愿意等待的最長時間。

4.4.3 雙目標選址模型

式（4）代表總運輸、儲存及訂貨成本；式（5）代表時間懲罰成本；式（6）表示一個需求點只能由一個儲備中心供應；式（7）表示儲備中心發生供應是其被選擇為前提；式（8）表示選取的儲備中心數量小于閾值；式（9）—式（11）為0-1變量。

5 實證分析

5.1 問題背景及數據獲取

目前，我國鐵路運營物資庫存管理均以鐵路局集團公司為單位開展，物資儲備分散管理會導致各貯存點之間調配難度大，閑置物資比重高，以及為了保障生產供應，每個貯存點的儲備庫存體量通常偏大，導致重復儲備庫存占用資金過高。所以，結合鐵路建設與運營點多、線長、面廣的特點，同一線路固定設備基本相同、配件基本通用的特點，選擇部分共性強且易于調配的物資進行跨鐵路局集團公司聯合儲備，通過區域劃分+區域內儲備中心選址的方法進行聯合儲備實施。

本文通過收集我國18個鐵路局集團公司聯合采購物資采購總額，以及相互之間的交通運輸距離及時間，并對數據進行了歸一化處理消除數據量綱影響。其中，18 個鐵路局分別為北京局、太原局、呼和浩特局、沈陽局、哈爾濱局、上海局、濟南局、南昌局、武漢局、鄭州局、廣州局、成都局、昆明局、南寧局、西安局、蘭州局、烏魯木齊局、青藏局。

5.2 改進方法選址求解

5.2.1 聯合儲備區域劃分

（1）確定聚類中心候選點。首先對18 個鐵路局的密度指數進行計算，選取排名前8的鐵路局作為聚類中心首選，分別為沈陽、北京、武漢、西安、上海、廣州、成都、太原。

（2）確定聚類數目。分別選取聚類數目為3-8，并計算每種聚類結果的組內平方和進行聚類效果評估，組內平方和隨聚類數目變化的曲線圖如圖2所示，從圖中可以明顯看出，當聚類數目k=6 時的組內平方和值最小，所以此時聚類效果最好，實現組內相似性高且組間差異性大的聚類效果。

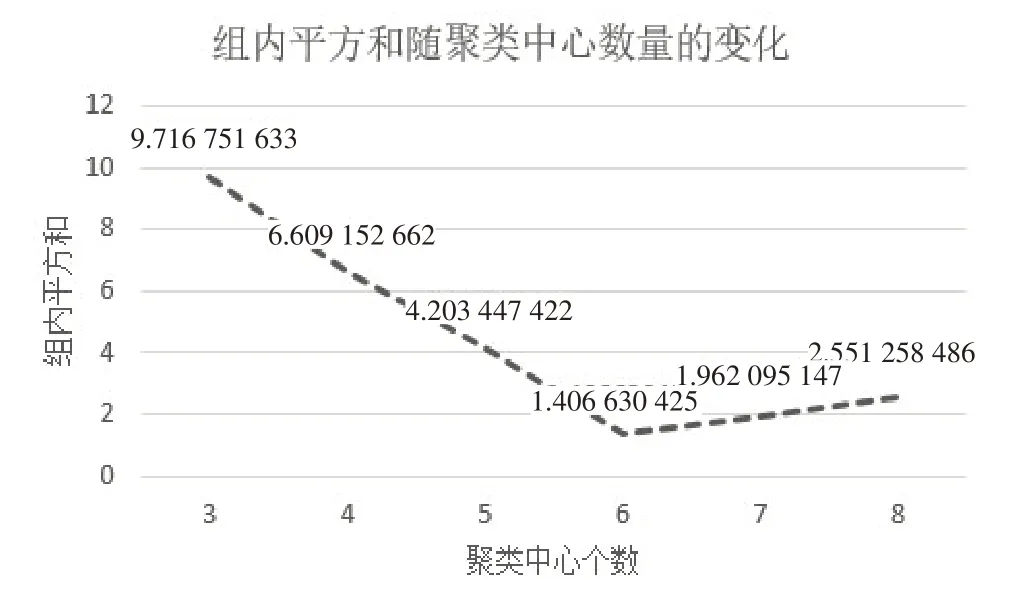
圖2 組內平方和隨聚類中心數量的變化

（3）聚類結果。確定最佳聚類個數后，根據改進的k-means 算法聚類，當k=6 時，聚類結果如圖3所示，具體見表2。

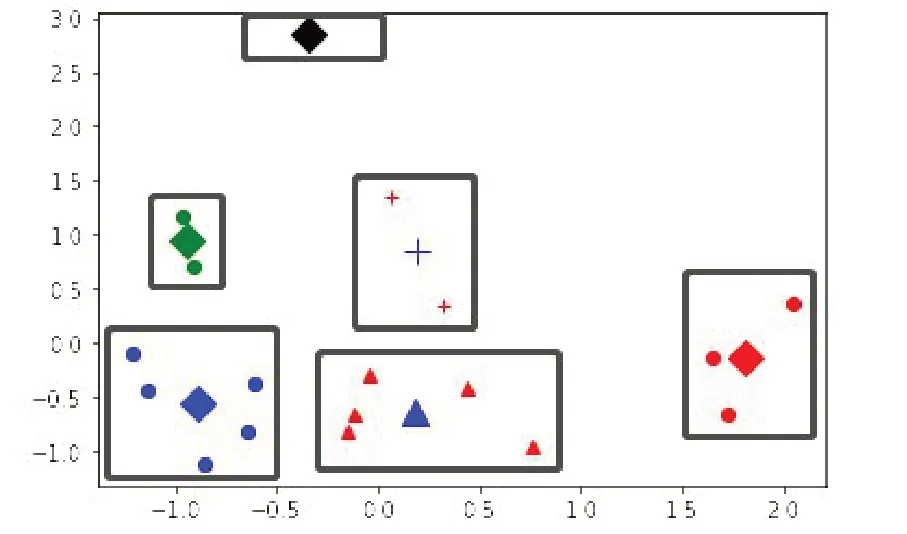
圖3 k=6時聚類結果

表2 k=6時聚類結果

5.2.2 區域內儲備中心選址

（1）參數設置。在得到區域劃分結果的基礎上，將繼續對各區域進行儲備中心選址，本文以機車車輛配件聯儲為例（共分為6 類，見表3，所以k=6）；單位時間懲罰成本a=300，cijk=ck代表運輸物資k 的單位運輸成本。

表3 鐵路機車車輛配件類別

假設所有需求點對同類物資的需求敏感系數相同(見表4)，所能接受的最長等待時間因物資需求計劃提報的差異性而有所不同，每個區域內符合設置儲備中心備選點條件的鐵路局數目見表5。

表4 物資需求敏感系數

表5 聯合儲備區域內儲備中心備選點選擇

（2）選址結果。本文運用matlab 對選址模型進行求解，由于區域1、4、6 符合條件的備選點只有一個，所以可直接得出結論。經過對其他3個區域逐一選址，得到選址計算結果（見表6），其中Z=Z1+Z2代表總成本。

通過對各區域內的計算結果比較，選取總成本最小的備選點作為最終儲備中心的選址位置，則選址結果見表7。通過將選址結果與聚類結果比較可以發現，聚類中心與最終的儲備中心選址結果只在少數區域有所不同，由于聚類分析中參數u=0.1，將物資需求相似性相對于距離因素對最終聚類結果的影響進行弱化，所以結合選址結果可以發現，若在空間分布上處于區域中心位置，并具有物資儲備及管理能力的鐵路局將會被選擇為區域聯合儲備中心的選址地點。

表6 儲備中心選址計算結果

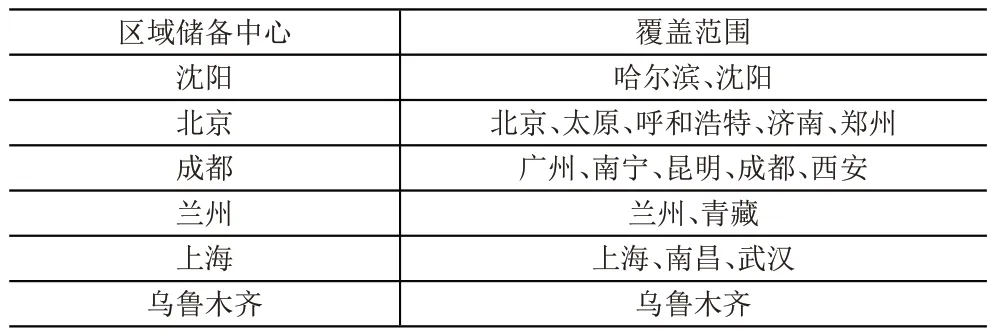
表7 區域儲備中心選址結果

6 結論

通過本文分析得到如下結論：基于問題背景對區域劃分及選址因素進行考慮，更能切實有效的解決問題。本文在鐵路物資聯合儲備管理的背景下，通過將距離因素與聯合采購額指標相結合對聚類方法的相似度進行衡量，對k-means 算法進行了改進。并基于鐵路物資需求需要保證供應的特點，構建了基于成本最小及保證供應的雙目標選址模型，并基于我國18 個鐵路局的實際數據，驗證了模型的有效性并實現了鐵路運營物資聯合儲備區域劃分及儲備中心選址，可為鐵路物資管理決策提供理論借鑒。但本文考慮的實際因素仍然有限，需要在以后的研究中結合實際因素對模型不斷修正，提高模型的精準性與實用性。