真問題·真研究·真收獲

潘智

[摘要]在小學數學教學中，教師依靠問題與學生進行互動和教學。合理的問題能更有效地提升數學教學質量，促進學生思維的發展。從一道易錯題入手，有針對性、有層次性、有啟發性地設計問題，借助結構化問題，引導學生深入探究，使學生達到理解算理、運用算法的學習目的。

[關鍵詞]結構化問題;余數;優化算法

[中圖分類號]G623.5 [文獻標識碼]A [文章編號] 1007—9068（2019）32—0008—03

所謂結構化問題，即在數學課堂教學中，以學生的知識經驗和現有數學能力為基礎，構建的一套有針對性、層次性和系統性的問題組。這里的“結構化”有兩層含義：一是環環相扣、層層遞進，問題之間有關聯性，用以有序激發、指導學生的數學探索活動;二是指問題有深度和廣度，在問題組的設計中，緊緊圍繞核心問題，縱向和橫向均有效發散，最后又回歸核心問題，促進學生構建完整的知識體系，提升學生的思維品質，發展學生的核心素養。本文以蘇教版教材四年級上冊“兩、三位數除以兩位數”的單元檢測中，學生的一道易錯題為例，探討如何在教學中應用結構化問題激起學生的研究熱情，激活學生的研究潛力，激發學生的探索精神。

一、核心問題為起點

數學教學活動必須建立在學生已有的知識經驗和認知發展水平之上，任何問題的提出也要以此為基礎，才能避免成為無源之水、無本之木。有道是“良好的開端就是成功的一半”，好的問題能激發學生的興趣，使學生產生好奇心和求知欲。同樣，好的問題也應抓住知識的本質、觸及知識的核心。因此，無論在何種情境之下，都要讓核心問題成為起點，讓學生站在自己的知識結構之上開展數學活動。

在“兩、三位數除以兩位數”的單元檢測中有一題“108÷28”，此題的本意是讓學生用豎式進行計算，小華同學卻運用簡便計算方法：

108÷28

=108÷4÷7

=27÷7

=3……6

這里利用了一個運算規律：a÷b=a÷c÷d（其中6=c×d）。4×7=28，所以108÷28=108÷4÷7沒錯;因為108÷4=27，所以108÷4÷7=27÷7也沒錯;27÷7=3……6同樣沒問題！但是正確的余數是24，究竟問題出在哪里？小華不解，所有人都覺得不可思議。

這不是教材中的內容，卻是數學學習中的“真問題”。這個問題的核心就是對算理的理解，產生兩種結果的原因就在于它們的算理不同。因此，我向學生提出了本次研究中的第一個也是核心的問題：“這樣的算法合理嗎？小華同學能解釋你做法的合理性嗎？”一石激起千層浪，學生的好奇心、好勝心被“點燃”，他們紛紛說出了自己的觀點和想法：

“我覺得余數是錯的，但是又不知道怎么說明。”

“我認為小華的算法是合理的，可余數為什么是6還是要通過生活中的例子來說明一下。”

“是的，除法就是平均分，我們可以用東西分一分啊！”

“108太多了，到哪里找這么多東西去分呢？”

提出問題后不一定立刻就要有答案，教師應該為學生提供一定的自主思考與探索的時間，使大部分學生都能經歷問題的解決過程，從而真正成為學習的主人。因此，我讓學生課后開展探究，可以與同學或父母進行合作，也可以自己動手試一試。

果不其然，第二天小華自己就有了發現：

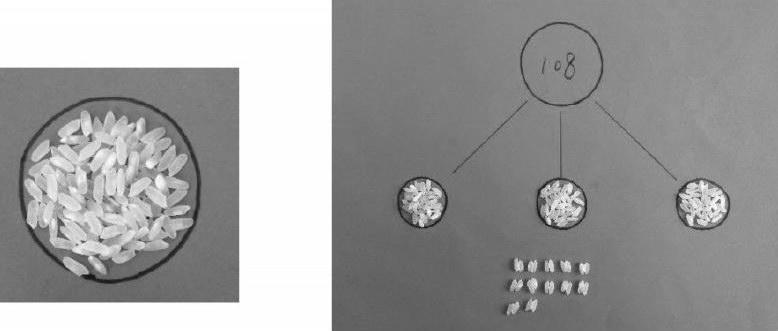
“昨天同學們提醒我，除法就是平均分，可以拿108個物體來分一分，但是這么多數量的東西不好找，所以我就想到了用108粒米來分。”

“我和爸爸首先根據108÷28的平均分意義，每28粒分一份，共分成了3份，還剩24粒，余數確實是24。”

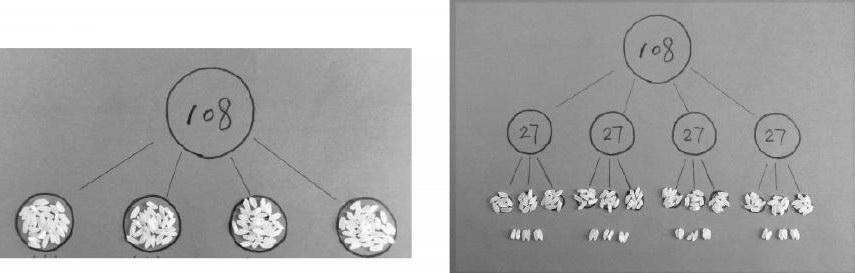
“接著按我的簡便算法來平均分，108÷28=108÷4÷7，先把108粒米平均分成4份，每份是27粒，再根據第二步算式‘27÷7將每7粒米分一堆，這樣每一堆都可以分成3份，剩6粒。”

“將兩次的結果一對比，就很容易發現：其實按照簡便計算的方法，最終剩下的總的余數（不在圓圈里的）也是24，余數6只是其中一份的余數，一共有4份，每份都余6粒米，所以正確的余數就是4×6=24。”

“我寫的6應該叫小余數，24才是大余數啊！”

“小余數”——這個名字真不錯！學生利用數形結合的方式探究核心問題，闡述了自己的算理與算法，提出“小余數”的概念，完成了真研究的起始工作。

二、關聯問題顯維度

提問就像是點亮明燈，能指引學生學習的方向，可探索知識的道路還是需要學生自己去尋找，實踐操作就是他們尋找的工具。在學生探索知識的道路上，這盞明燈所能照到的地方越多，學生的思維就越廣闊，思維品質就越能得到有效的鍛煉。這時，要依靠從核心問題引申出的、有層次性的、有針對性的多維度問題，幫助學生明晰算理、厘清思路、拓展方法。

為了對“小余數”進行“真研究”，我引導學生從以下幾個問題開始探究。

問題一：每一個這樣的計算都會有“小余數”嗎？“小余數”和“大余數”之間有聯系嗎？

“我們列舉出這么多算式，它們兩種計算方法得到的余數確實都不一樣，一個大的，一個小的，真的有‘大余數和‘小余數之分了。”

“‘小余數雖然不是正確的余數，但是分米粒時已經說得很清楚，所有的‘小余數加起來就是‘大余數。我認為遇到有余數的題目完全可以用這樣的簡便方法進行計算，只是最后要把‘小余數乘第一個除數才能得到‘大余數。

108÷28=3……24.

108÷28=108÷4÷7=27÷7=3……6：

252÷32=7……28.

252÷32=252÷4÷8=63÷8=7……7：

570÷35=16………10，

570÷35=570÷5÷7=114÷7=16……2;

999÷12=83……3，

999÷12=999÷3÷4=333÷4=83……1。

如6×4=24、7×4=28、2×5=10、1×3=3等，道理也很簡單，因為‘大余數是按照第一次除法的份數去平均分的，所以第一次的除數是幾，‘小余數就有幾份。”

問題二：有的小組舉例428÷63=428÷7÷9，可是第一步計算428÷7時就有余數，像這樣第一步就產生余數的算式，還能簡便計算嗎？如果能，“小余數”和“大余數”之間又有怎樣的關系？

第一次研究時，有近一半的小組遇到了同樣的困難，只是他們及時更換了數據。新的問題讓他們重新回到深度研究之中。雖然有點難度，但是學生很快還是有了發現，如圖：

“這是根據小華的分米粒想到的辦法，我們小組嘗試畫圖來表示。從圖中可以看出，先算428÷7將428平均分成7份，每份是61，余數為1;接下來應該將7個61都按每9個一份進行平均分，每個61都可以平均分成6份，余7個。因此最終商為6，余數一共有7×7+1=50，這答案與用豎式計算的結果是一樣的。”

“其實就是正常一步步地計算，只不過第二次計算時是用第一次得到的商繼續除，余數先放到一邊，最后還原成‘大余數時，一定要把這個第一次得到的‘小余數加上。”

“我們小組一開始寫的1001÷32也可以簡便計算。我口算了一下，先算1001÷4等于250余1，把‘小余數1放一邊，再算250除以8得到31余2，那么‘小余數2乘4再加1等于9，最終的答案就應該是31……9。”

“老師，我在想，剛才都是把一個除數變成兩個除數，能變成三個、四個除數嗎？”

瞧，水到渠成后，學生代替教師提出了更深層次的問題。

問題三：像375÷24這樣的算式，能變成375÷2÷3÷4加以計算嗎？借助“小余數”能算出正確的“大余數”嗎？

沒多久，更復雜但是又很有條理的算理圖就被學生畫了出來，如圖：

“根據我們研究出的方法，先算375÷2=187……1，‘小余數1放一邊記下;再算187÷3=62……1，這里的1乘2后也記下;接著再算62÷4=15……2，我把這里的2叫作“小小余數”，要用2×2×3=12記下;最后用三次得到的1+2+12=15，得出375÷24=15……15。”

學習數學知識不僅要理解其核心問題，更重要的是要理解各知識點之間的關聯，以便于形成立體式的知識結構。三次探討“小余數”和“大余數”關系的過程，是層層遞進提問、步步剖析算理的過程。這幾個問題循序漸進，指引學生思維不斷發展。學生通過動腦、動手和動口，探究算法，經歷了知識的形成過程，積累了活動經驗。

三、優化問題有收獲

比較是促進思維發展的重要手段，對比可以幫助學生找出知識之間的差異與聯系，提高學生的觀察能力、思維能力、運算能力等。盡管學生在操作中掌握了算理，但是算法的對比和優化不能忽略，這將是提高學生運算能力的有力保障。

“這樣的計算方法與豎式計算相比，你更喜歡哪一種呢？為什么？”這個問題讓學生開始了新的討論，他們交流各自答案并說明理由，有的學生仍喜歡豎式計算，有的學生覺得小華的方法更簡單，可以直接口算，也有的學生表示都喜歡，要合理使用。這時，可安排學生共同出題，并分別用兩種方法進行計算比賽。通過計算比賽，學生感受并驗證每種方法的優勢與不足，達到優化算法、提高運算能力的效果。

算理是本次研究的核心問題，是問題的開始，也應該是問題的延續。根據學生的掌握情況，我又提出了新的要求：“既然這兩種方法都合理，那么它們的結果怎樣才能表示成同樣的形式？”這個問題直指算理本質，目的是進一步拓展學生的思維深度：有的說直接寫3……24，有的說可以用3……6×4表示，還有的想到了小數。經過討論，大家一致同意用小數表示更合理，且嘗試用計算器計算了108÷28和108÷4÷7=27÷7的最終答案，發現顯示的結果都是相同的。于是大家又計算了其他算式加以驗證，并在此基礎上進一步明確：進行平均分時，剩下的余數還可以不斷地分下去，就產生了小數，只不過小數計算還沒學到，但是可以用計算器證明無論是豎式計算還是簡便計算，如果一直平均分下去，最終的結果都是一樣的，所以這兩種方法都是正確的。

學生在數學學習中會產生許多疑問，正如小華的錯解帶來的疑惑，這時教師就可以開展數學活動，引導學生借助生活經驗去嘗試、去發現。每一次活動都應該從問題開始，同時產生新的問題，并不斷探索下去，最終找出問題的本質，獲得真理。一道常規的豎式計算題，卻因為一位學生的簡便計算而讓知識間產生了交集，其中的錯與對使學生對知識有了新的感受，產生了真問題;師生帶著問題進行思考與探索，在經歷數學活動的過程中，創造出了“小余數”這個聞所未聞的新概念;層層遞進的結構化問題讓學生的思想發生碰撞，分與合的雙向思維成功提高了學生的運算能力;同時，問題火花的飛濺使得內容不斷豐富、問題意識不斷延伸、智慧研學不斷開花結果。面對學生認知的新問題，教師要有效設計問題，舍得花時間、愿意給空間，讓學生開展真研究，去觸摸知識的本源、探尋思維的路徑、提升學習的品質，實現真收獲！

（責編 金鈴）