借助直觀教學，促進“數與代數”的深度學習

閆雯雯

[摘要]直觀教學是指借助圖形直觀、實物直觀或符號直觀描述幾何或者其他數學問題，探索解決問題的思路，可以把復雜的數學問題變得簡明、形象，適應小學生的思維水平。在“數與代數”中借助直觀教學，不僅能讓學生對于概念的理解更為清晰，對于算理的理解更為深刻，還能強化規律記憶，不斷發展學生的高階思維，促進學生深度學習。

[關鍵詞]直觀教學;數與代數;深度學習

[中圖分類號]G623.5 [文獻標識碼]A [文章編號]1007—9068（2019）32—0037—02

如今的教育領域，“深度學習”逐漸成為熱門且時髦的話題。“深度學習”是指學習者先根據自己的興趣和需求，在完全認識和充分理解的基礎上，主動地、批判性地學習，并能夠運用多樣化的學習策略來深度加工知識，聯系前知、思考后知，建立完整的知識體系，再綜合運用、有效遷移，從而解決一些學科上或是生活中的復雜問題的學習。簡而言之，深度學習就是一種主動的、探究式的、理解性的學習方式，要求學習者進行理解性的學習、深層次的信息加工、批判性的高階思維、主動的知識建構和知識轉化、有效的知識遷移及真實問題的解決。

“幾何直觀”是課程標準中新增加的核心概念，是眾多教育者關注的問題。數學本身是抽象的，而借助直觀教學，能夠使復雜的數學問題變得形象直觀，更容易啟發學生，促進學生數學思維的不斷發展。直觀教學能幫助學生更好地理解數學本質和促進學生思維的發展，通過圖形、實物、符號等直觀形象，幫助學生把復雜、抽象的數學問題變得簡明、形象，從而促使學生能夠主動地發現和探索問題，批判性地思考和解決問題，最終促進學生深度學習。

小學數學共分為四大領域：數與代數、圖形與幾何、統計與概率、實踐與綜合應用。“數與代數”是其中比重最大的部分。“數與代數”的學習于學生而言既枯燥乏味，也難以理解的，所以如果在“數與代數”的教學中能夠借助幾何圖形，學生學習的效率一定會有很大程度的提高，學生的深度學習也能得到促進和發展。下面筆者以“數與代數”的教學為例，從圖形直觀、實物直觀和符號直觀三個方面展開論述。

一、借助圖形直觀，清晰概念認識

在“數與代數”這一板塊中，概念教學占了很大比例。德國哲學家康德認為：“缺乏概念的直觀是空虛的，缺乏直觀的概念是盲目的。”學生對于概念的學習和理解是淺層次的，這可能跟學生的思維水平和能力有關，他們的形象思維占主導地位，對知識的理解需要建立在豐富的直觀表象之上。運用幾何直觀，可以把教材中抽象的、空泛的、靜止的數學概念動態化、形象化地呈現出來，這樣更有助于學生深入地理解所學習的內容。把文字語言轉化為圖形語言，不僅降低了學生認識的難度，也促使學生對概念的理解更清晰、更全面、更深入。

如在“數的認識”中，分數的認識是比較抽象、難以理解的內容，是學生認識整數之后，第一次數域的擴充。在學習蘇教版教材三年級上冊第七單元“分數的初步認識”時，學生之前認識的只是萬以內的整數，他們對于分數這種由三部分組成的數，在思維上是有認知障礙的。因此不妨借助幾何直觀，再加上學生已有的平均分的學習經驗，把靜態的分數表示轉化成動態的平均分的過程，充分展現分數的三部分表示的含義，幫助學生突破學習障礙，清晰對概念的認識和理解。

教學片段1：分數的初步認識（一）

認識二分之一：在情境中認識一個蛋糕的二分之一之后，教師提出：“同學們，你們已經認識了二分之一，現在讓我們來創造一個二分之一好嗎？請拿出一張長方形紙，折一折，用彩筆給它的二分之一涂上顏色。”不同的折法（如圖1）讓學生感受到，無論怎樣折，只要把這個長方形紙平均分成2份，每份都是它的二分之一。借助圖形直觀，把二分之一這個分數的分子、分母和分數線表示的具體含義展示出來，很好地幫助學生去理解二分之一。

認識幾分之一：充分認識二分之一之后，教師繼續激趣：“你還想認識幾分之一呢？請拿出另一張老師給你們準備的紙折一折，并取其中一份涂色表示你創造的分數。”在展示中學生發現：不管是正方形還是圓形，只要把這張紙平均分成4份，每份就是它的四分之一……不管什么圖形，只要把它平均分成幾份，每份就是它的幾分之一。學生通過直觀圖形深刻理解了分數就是“平均分后占總份數中的一份”。

分數的概念本身是抽象的，但又是學生在認數過程中必須要學習的非常重要的一類數。之后學習分數的計算、小數的認識、百分數的認識等，都是基于分數的認識的延展。因此，在教學中，教師應積極借助圖形直觀來動態演示，幫助學生突破認知障礙，清晰學生對分數的認識。只有具有理解性、探究性、創造性的學習，才能促進學生的深度學習。

二、借助實物直觀，深刻算理理解

計算是小學生需要熟練掌握和運用的一項技能。很多時候，教師會設置強化技能訓練，通過持續性地、高強度地計算練習，希望學生能夠形成一定的技能。其實計算課的教學更應關注學生對算理的理解：“為什么這樣算？”“這樣算表示什么含義？”學生只有在充分理解算理的基礎上才能夠自然運用，熟練掌握，也才能夠避免機械性地做題。在計算教學中，同樣可以借助實物直觀，把抽象的、難以理解的算理巧妙地借助實物（如小棒、計數器、算盤等）表現出來，讓學生溝通算理與算法之間的內在聯系，深刻理解算理，逐步內化算法，真正形成自己的技能。

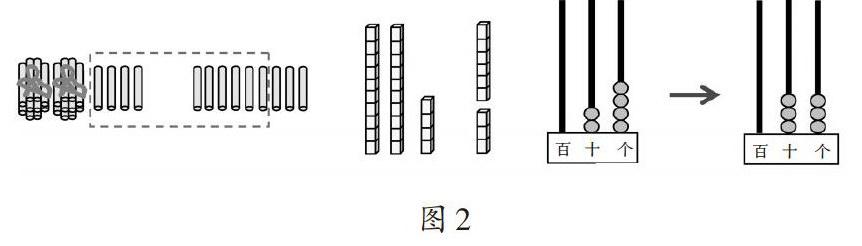
教學片段2：兩位數加一位數（進位）

教學時教師先根據問題列出算式“24+9”，再拋出問題：“這道算式可以怎樣計算呢？請同學們借助學具自主探究。”教師提供小棒、小方塊、計數器、算盤等這些常用的學具，輔助學生探究算法。學生通過匯報、演示（如圖2）發現，不管是小棒、小方塊還是計數器，24加9，滿十都要向前一位進1，這樣就溝通了算理和算法之間的內在聯系。

這部分是蘇教版教材一年級下冊第六單元第一課時的教學內容，為接下來學生學習多位數的加法，特別是需要進位的加法打下了堅實的基礎。而學生在遇到需要進位的計算時往往容易出錯，這在很大程度上歸咎于對之前的“滿十進一”的算理沒有充分的理解。因此，借助不同的實物，把算法直觀地展示出來，可幫助學生厘清算理，同時讓學生主動地進行知識的建構，促進深度學習。

三、借助符號直觀，強化規律記憶

規律的探索和運用是小學數學教學的必經之路，而運算律（加法交換律、加法結合律、乘法交換律、乘法結合律、乘法分配律）就是運算中常用的規律。

蘇教版教材四年級下冊將運算律作為一個獨立單元，旨在突出運算律在數與代數領域的重要性，要求學生能夠充分理解運算律并能靈活運用這些規律解決問題。這也是在為學生學習五年級的小數和分數的簡便計算打下基礎。然而，學生對于乘法和加法的運算律的理解和記憶存在一定的困難：理解和記憶不深刻，運用也就不靈活。為此，教師要把運算律和一些符號、圖形結合起來，幫助學生強化理解和記憶運算律。

教學片段3：運算律的整理與練習

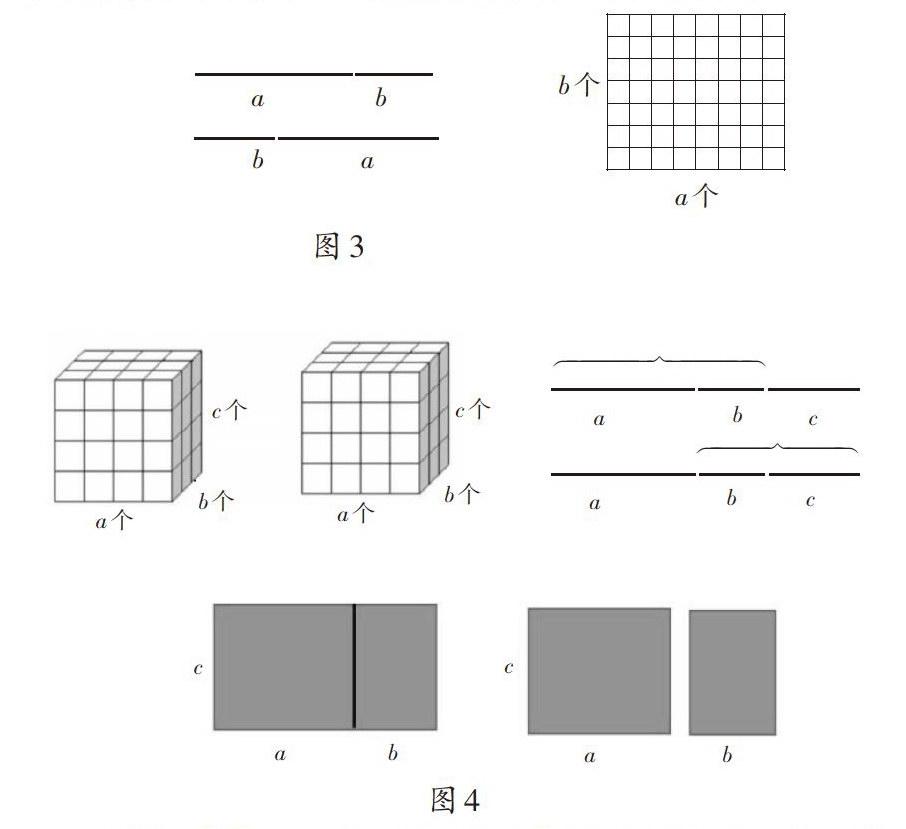
在整理運算律相關公式之后，教師提問：“還能用什么表示運算律？你能想到什么運算律？”并出示圖3，指出：兩張圖分別對應加法交換律和乘法交換律。接著讓學生小組合作探究“還能用哪些圖表示其他的運算律”。小組匯報畫圖結果和對應的運算律如圖4所示：

小結：線段可以表示加法交換律和結合律，平面圖形可以表示乘法交換律和分配律，立體圖形可以表示乘法結合律。

最后借助圖形，拓展知識內容。教師提問：“這里還有兩張圖（如圖5），你能發現其中的運算律嗎？”從而引出減法的性質。

教師把加法的運算律和線段的加減相結合，把乘法的運算律和長方形的面積、長方體的體積計算相關聯，不僅幫助學生深刻理解和記憶這些規律，也潛移默化地促進了學生對知識的遷移和深度學習。

“數與代數”領域的知識抽象度高，邏輯性強，對于適合在具體活動和實際摸索中思考問題的學生來說，直觀教學可以化解代數知識的抽象性，便于他們理解、掌握和應用，促進他們的深度學習。

（責編 羅艷）