融入數學建模思想的線性代數案例教學研究

劉敬剛 郭燕

摘 要：針對線性代數課程傳統教學方法中存在的不足，提出將數學建模思想融入線性代數案例教學過程的新思路.通過具體例子表明，在案例教學中貫穿數學建模思想，可以使抽象的線性代數理論、方法變得具體、形象、直觀，加深學生對所學內容的理解，同時培養學生分析問題和解決問題的能力，提高學生的綜合素質和創新能力，激發學生的學習興趣，保證教學質量.

關鍵詞：數學建模;線性代數;教學方法;案例教學

中圖分類號：G642.0? 文獻標識碼：A? 文章編號：1673-260X（2020）01-0015-03

1 前言

線性代數作為理工科大學生的一門必修數學基礎課，它在數學、物理、工程技術等方面具有廣泛應用[1].隨著計算機技術的日益普及和廣泛應用，現代工程問題的解決最終都轉化為線性代數方程組的求解問題，因此線性代數的理論和方法在大學生走上工作崗位后，有著十分廣泛的應用.線性代數的核心內容是以矩陣為工具研究向量、向量空間、線性變換和線性方程組，這些內容比較抽象且理論性強，對于剛跨進大學校門的學生而言學習難度較大[2].同時由于線性代數課程設立之初，以介紹理論為主，教學實踐中偏重自身理論體系的完備，強調定義、定理、性質等理論內容，而對線性代數的方法和具體應用不夠重視，很少涉及具體應用實例，增加了大學生理解線性代數理論方法的難度.隨著廣大教育工作者通過線性代數課程的教學研究和教學改革，人們逐步認識到線性代數理論方法和實際應用相結合的重要性，但是在課堂教學中普遍存在以教師為主導的案例講解僅僅說明線性代數有用，并沒有讓抽象的理論內容變得直觀[3-5].當前“新工科”理念要求，課堂教學既能發揮教師的主導作用，又能充分體現學生的主體地位，實現課堂教學的“去中心化”[6].針對這種現狀，本文提出將數學建模思想融入線性代數應用案例教學過程中，通過“教師引導、學生主導”重現問題分析、問題簡化、建立模型、求解模型、結果解釋和驗證整個過程，讓學生看到線性代數理論方法“有用”，同時培養學生應用所學知識分析、解決問題的能力，也為理解線性代數的抽象概念和方法提供有效途徑.

2 數學建模思想融入案例教學的方法

面向實際問題，融合數學建模思想，依據線性代數有關理論建立數學模型，并應用線性代數方法進行求解，使原本抽象的理論、方法變得生動有趣，可以有效激發學生的求知欲，提高學習的積極性和學習效率.眾所周知，數學建模的基本步驟為：分析問題、模型假設、符號說明、建立模型、求解模型、結果分析、模型檢驗等，下面以飲料配制問題為例介紹數學建模思想融入線性代數案例教學的設計方法.

例：飲料配制問題

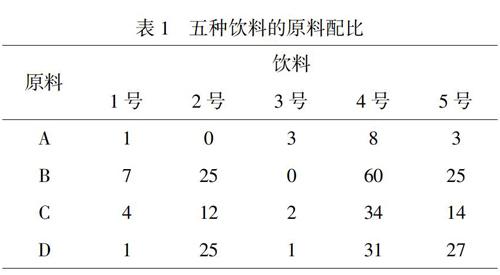
某飲料廠用原料A、B、C、D，按不同配比制成五種飲料（編號為1-5），具體原料配比見表1.某日，飲料廠第4號和第5號飲料售罄.問題：能否用其他飲料配制出這兩種脫銷的飲料？若可以，應該如何配制？

對于這樣一個實際問題，一定會引起同學們的興趣，可以極大地調動同學們對問題的探知欲望.依托數學建模思想，將數學建模基本步驟和線性代數理論方法有機結合在一起，具體分為七個步驟實現對問題的有效解決.為了敘述方便，首先考慮4號飲料的配制問題，5號飲料類似進行討論.

1.問題分析

要配制出4號飲料，只需要討論1、2、3號飲料，能否按某種比例混合后，滿足4號飲料對四種原料的配比要求.

2.數據處理并提出具體問題

根據表1的數據，首先求出五種飲料在配比表中的列和，如表2所示.從而可以提出如下具體問題：假設要配制133單位的4號飲料，能否由1、2、3號飲料混合達到4號飲料的配比要求，如果能求出混合比例.

3.模型假設

假設原料可分.

4.符號說明

規定五種飲料在表2中的原料配比列和所示容量為一份飲料.設配制1份即133單位的4號飲料，需要飲料1、2、3分別為x1份、x2份、x3份.

5.模型建立

由已知信息建立如下數學模型

x1+3x3=87x1+25x2=604x1+12x2+2x3=34x1+25x2+x3=31? （1）

從而將4號飲料能否配制的問題，轉化為非齊次線性方程組（1）是否有解的問題.

6.模型求解

由線性代數關于線性方程組解的存在性判定有關方法和結論，首先利用矩陣的初等行變換將線性方程組的增廣矩陣化為行階梯形矩陣，

因為R（A）=R（A，b）=3，所以有唯一解，即4號飲料可以由1、2、3號飲料配制且配制方法唯一.

進一步，用初等行變換將增廣矩陣化為行最簡形，

解得x1=5，x2=1，x3=1.

7.結果解釋

要配制133單位的4號飲料，分別需要1、2、3號飲料5份、1份、1份，即5份13單位的1號飲料、1份62單位的2號飲料、1份6單位的3號飲料混合可得133單位的4號飲料.

8.應用

綜上，可知配制1單位的4號飲料，1、2、3號飲料分別需要，從而得1、2、3號飲料的混合比例為65：62：6.

以上過程針對4號飲料的配制問題，在數學建模思想指導下完成了對問題的求解.同理，假設要配制出一份即69單位的5號飲料，需要飲料1、2、3分別為y1份、y2份、y3份，建立如下數學模型

x1+3y3=37y1+25y2=254y1+12y2+2y3=14y1+25y2+y3=27? （4）

用矩陣初等行變換化增廣矩陣為行階梯形，可得

因為R（A）

飲料配制問題的求解過程中，教師用數學建模思想方法引導學生，應用線性方程組有關理論和方法分析問題、解決問題，突出了學生的主體地位.整個過程類似中學解應用題，大學一年級同學接受起來比較容易，但是其中蘊含著豐富的數學建模思想，具體有以下幾個方面：

1.對問題進行分析，由已知數據信息求表1中原料配比的列和，豐富完善數據信息;

2.對問題進行必要的合理假設，即假設配料可分，該假設既符合實際又方便求解;

3.為了建模直觀、方便起見，假設需要配制的飲料總量為1份，即表2所示飲料在原料配比表中的列和，從而得到簡化的具體問題;

4.數學模型就是由賦予特定含義的數學符號，給出的數學表達式.

5.結果解釋中，準確解釋了的求解結果的具體含義，并且為了配制方便，將配比轉化為在同一度量單位下飲料的混合比例.

依托數學建模思想方法，搭建了連接線性代數和實際問題的橋梁，將學和用自然結合、相輔相成，學為用作必要準備，用體現學的價值，充分調動了學生學習線性代數的積極性和主動性，提高了對線性代數理論方法的學習熱情.

3 教學案例賦予抽象概念直觀解釋

線性代數中的向量、向量的線性表示、向量組的線性相關性和向量空間等概念比較抽象，當向量維數較高時沒有相應的幾何解釋，給學習和理解有關定義、結論和方法造成了很大困擾.注意到飲料配制問題中五種飲料的配比都是有序數組，因此可以用向量來表示，記為

由（6）式可以看出，4號飲料能否由1、2、3號飲料配制的問題，就轉化為向量？琢4能否由向量組？琢1，？琢2，？琢3線性表示的問題.換言之，就是？琢4是否屬于？琢1，？琢2，？琢3生成的向量空間

又由于R（？琢1，？琢2，？琢3）=R（A）=3，所以向量組？琢1，？琢2，？琢3線性無關，是向量空間L（？琢1，？琢2，？琢3）的一組基.由問題（1）的求解結果可知？琢4可由向量組？琢1，？琢2，？琢3線性表，即？琢4∈L（？琢1，？琢2，？琢3），或者說？琢1，？琢2，？琢3，？琢4線性相關.同理分析可得，？琢5不能由向量組？琢1，？琢2，？琢3線性表，即？琢5？埸L（？琢1，？琢2，？琢3），或者說？琢1，？琢2，？琢3，？琢5線性無關.

總之，通過將飲料配制問題的數學模型寫成向量形式，賦予向量、線性表示、線性相關性和向量空間等抽象概念具體的實際含義，對于抽象內容的學習和理解提供了幫助.

4 結論

在線性代數課程教學中開展融入數學建模思想的案例教學，有利于將線性代數理論方法和實際應用有機結合起來，有利于將線性代數知識的“學”和“用”有機結合起來，有利于將專業基礎知識教育和學生綜合素質、創新實踐能力培養有機結合起來.通過案例教學，使線性代數理論方法在數學建模思想方法指導下成為解決實際問題的有效工具，不僅加強了學生對線性代數知識點的理解和掌握，更教給學生一種解決實際問題的方法，使學生養成良好的分析問題、解決問題習慣，掌握開啟成功大門的鑰匙.

參考文獻：

〔1〕朱琳，蔣啟芬.國外線性代數的教學研究述評[J].數學教育學報，2018，27（01）：79-84.

〔2〕文軍，屈龍江，易東云.線性代數課程教學案例建設研究[J].大學數學，2016，32（06）：46-52.

〔3〕付傳秀，周建新.線性代數教學改革中融入數學建模思想的探討[J].教育教學論壇，2019（21）：110-111.

〔4〕李清華.數學建模思想有效融入線性代數教學的探析[J].教育現代化，2018，5（39）：77-79.

〔5〕段勇，黃廷祝.將數學建模思想融入線性代數課程教學[J].中國大學教學，2009（03）：43-44.

〔6〕謝加良，朱榮坤，賓紅華.新工科理念下線性代數課程教學設計探索[J].長春師范大學學報，2018， 37（04）：131-133+138.