基于層次分析數(shù)學模型的高職教學質(zhì)量評估的研究與實現(xiàn)

曾龍英

摘? 要：層次分析法是系統(tǒng)分析的重要工具，其基本思想是把問題層次化、數(shù)量化，并用數(shù)學方法求解，為分析、決策、預報或控制提供定量依據(jù)。層次分析主要通過數(shù)學的方式定量地分析難以量化，又相互關(guān)聯(lián)、相互制約的眾多因素構(gòu)成的復雜問題。本文通過研究教學質(zhì)量的評估，建立層次分析的數(shù)學模型，以教學評估量化為目標。建立層次結(jié)構(gòu)及數(shù)量化，系統(tǒng)地分析教學質(zhì)量評估方法，科學嚴謹?shù)孬@得定量的決策數(shù)據(jù)。

關(guān)鍵詞：層次分析? 數(shù)學模型? 教學質(zhì)量? 評估方法

中圖分類號：G64? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ?文章編號：1674-098X（2020）09（b）-0193-03

Abstract： Analytic hierarchy process（AHP） is an important tool of system analysis. The basic idea is to level and quantify problems， and to solve the problems by mathematical method. It provides quantitative basis for analysis， decision-making， prediction or control. The analytic hierarchy process （AHP） mainly uses mathematical methods to analyze replication problems quantitatively which are difficult to quantify， interrelated and constrained. In this paper， by researching the evaluation of teaching quality， the mathematical model of AHP is established to quantitative teaching evaluation. In order to systematically evaluate and analyze teaching quality， the AHP is established to get the quantitative decision data scientifically and rigorously.

Key Words： Analytic hierarchy process; Mathematical model; Teaching quality; Methods of evaluation

在高職院校的教學管理工作中，教學質(zhì)量的評估是院校建設(shè)重要的組成部分，也是院校決策的重要依據(jù)。教學質(zhì)量的評估不但包括教師的綜合素質(zhì)，同時也包括學生層次和院校教學的硬件條件。通過教學質(zhì)量的評估，不但可以知道院校工作的成績，還是找差距定方向的重要依據(jù)，可以調(diào)整和優(yōu)化教學質(zhì)量方案，從而提高院校的人才培養(yǎng)能力。而在傳統(tǒng)的教學管理中，由于缺少對教學信息的系統(tǒng)分析，往往只是采用調(diào)查問卷的方式來獲取教師教學評價信息，不能定量、嚴謹?shù)胤治鰯?shù)據(jù)。

高職教育的核心是培養(yǎng)高級藍領(lǐng)技能型人才的搖籃，教學質(zhì)量比院校的科研能力更重要，直接決定了院校建設(shè)的質(zhì)量，決定了畢業(yè)學生的綜合質(zhì)量。因此為保障高效的教學質(zhì)量，通過數(shù)學建模，采用科學嚴謹?shù)募夹g(shù)手段，建設(shè)教學質(zhì)量評估系統(tǒng)，能有效地對教師教學質(zhì)量進行把控，為提升高職院校教學整體實力提供數(shù)據(jù)支撐，提供可靠的決策依據(jù)。通過對教學質(zhì)量評估數(shù)學模型的建立，可以為提升高職院校的教學管理提供更加合理的建議，從而對教學管理工作進行改善優(yōu)化。

1? 層次分析法的基本步驟

層次分析法（Analytic Hicrachy Proccss 簡寫為AHP），它是將半定性、半定量的問題轉(zhuǎn)化為定量計算的一種行之有效的方法。把復雜的決策系統(tǒng)層次化，通過逐層比較各種關(guān)聯(lián)因素的重要性組建模型，為分析和決策提供定量的依據(jù)。層次分析法是將決策問題按總目標、各層子目標、評價準則等方案的順序分解為不同的層次結(jié)構(gòu)，然后用求解判斷矩陣特征向量的辦法，它特別適用哪些難于完全用定量進行分析的復雜問題。

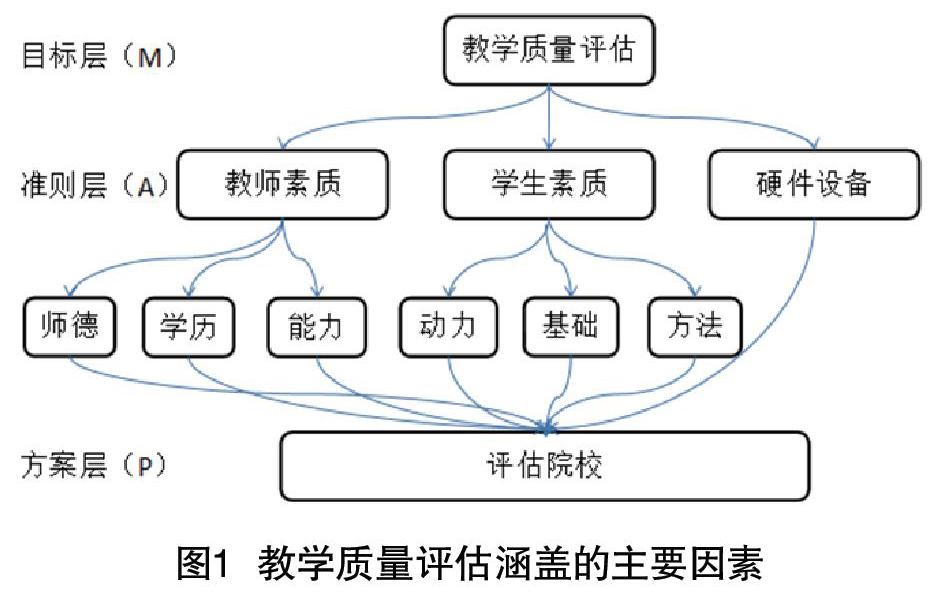
（1）分析系統(tǒng)中各個元素之間的關(guān)系，建立系統(tǒng)的遞階層次結(jié)構(gòu)，在系統(tǒng)分析方法中通常將問題分成三個層次：第一層是最高層，這一層描述的是分析問題的預定目標或理想結(jié)果，也稱目標層;第二層是中間層，它是為實現(xiàn)目標所涉及的主要因素、策略和準則，組成了問題分析的不同方向，是最高層的進一步分析，也稱準則層;第三層是最底層，這一層實現(xiàn)目標所涉及的各種條件、決定的因素和措施方案等，也稱方案層。

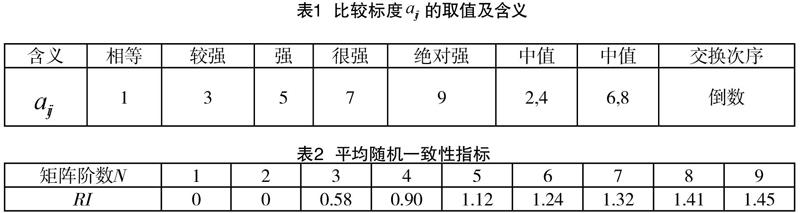
（2）構(gòu)造兩兩成對比較的判斷矩陣，成對比較可以提高諸因素比較的準確程度。假設(shè)有個元素對目標有影響，從而確定各因素在對的影響中所占的相對重要性。每次取兩個因素和，用表示與對目標的程度之比，按1～9的比例標度（1～9標度方法是美國運籌學家Saaty通過事實和科學依據(jù)證明是可行的，并能較好地將思維判斷數(shù)量化，見表1來度量，個元素彼此比較，便構(gòu)成了一個兩兩比較的判斷矩陣模型，判斷矩陣具有的性質(zhì)，具有上述性質(zhì)的矩陣為正互反矩陣。如果矩陣滿足，則稱為一致性的判斷矩陣。

（3）層次單排序及其一致性檢驗，為了更好地獲得模型的正確的結(jié)果，需要檢驗判斷矩陣的一致性。假設(shè)一個要研究的目標是一個由不同的小目標（）一步步實現(xiàn)的大目標，的價值由各個小目標價值的實現(xiàn)決定。每個小目標的價值是，每個小目標價值所占的比重，價值與所占比重的比為，這樣得到判斷矩陣

根據(jù)正互反矩陣的性質(zhì)，有特征根，其余的特征根為零對應的特征向量為，則。定義衡量矩陣不一致性的指標和平均隨機一致性指標RI，如表2所示（表2是Saaty通過500個隨機樣本矩陣計算得到平均隨機一致性指標RI）。

令，定義CR為一致性比率，當CR<0.1時，判斷矩陣具有滿意的一致性，否則就需要調(diào)整判斷矩陣，使之具有滿意的一致性。

2? 教學質(zhì)量評估數(shù)學模型的建立與實現(xiàn)

（1）建立數(shù)學模型，為了解決教學質(zhì)量評估的方法，首先構(gòu)建符合層次分析方法的模型，分析問題組成的元素。高職教育質(zhì)量的優(yōu)略有很多因素組成，本案例主要分析組成教學質(zhì)量的教師素質(zhì)、學生素質(zhì)和教學設(shè)備條件，三個方面進行分析和計算。按照層分析的方法構(gòu)造層關(guān)系，如圖1所示。

（2）采用層次分析數(shù)學模型計算。先進行層次單排序及其一致性檢驗，然后是層次總排序的一致性檢驗和計算組合權(quán)重。

①建立準則層對目標層的成對比較判斷矩陣，并求最大特征根、特征向量和一致性指標。

通過方根法近似計算得特征向量，

計算最大特征根，計算一致性指標，查表2得到相應的隨機一致性指標RI=0.58（），計算一致性比率，小于0.1，判斷矩陣具有滿意的一致性。

②建立方案層對準則層的成對比較判斷矩陣，并求最大特征根、特征向量和一致性指標。

CR均小于0.1，判斷矩陣具有滿意的一致性。

③進行層次總排序的一致性檢驗和計算組合權(quán)重。計算一致性比率：

因為小于0.1，判斷矩陣具有滿意的一致性。

于是通過層次分析法得出了各具體評價指標的權(quán)重。

最后需要再將各個具體的評價指標劃分為若干個數(shù)量等級，如A、B、C、D級，分別對應100、80、60、40分，等級的高低決定了在最終分數(shù)中所占的比重。最后加權(quán)的綜合評估值（N）可以用如下公式計算：

其中分別為教師素質(zhì)和學生素質(zhì)所對應的數(shù)量評價等級，為教學設(shè)備的數(shù)量評價，分別是相對應的組合權(quán)重，為教學設(shè)備的權(quán)重。

3? 結(jié)語

教學質(zhì)量的評估，影響因素涉及多個方面，甚至在不同的專業(yè)，不同的院校影響因素、權(quán)重都有所不同，在做評估時，有些因素的重要性，影響力，或者優(yōu)先程度往往難以標準地量化，人的主觀選擇會起到一定的作用。但隨著系統(tǒng)工程的觀念越來越被理解和接受，客觀、定量的數(shù)據(jù)分析成為各個領(lǐng)域的主流，傳統(tǒng)的教學質(zhì)量的評估難于完全定量地分析。層次分析法把不能定量的問題抽象描述、簡化，形成數(shù)學模型，通過與決策目標有關(guān)的元素分解成目標、準則、方案等層次，在此基礎(chǔ)之上進行定性和定量的分析，獲得最優(yōu)的決策方法。本文通過分析教學質(zhì)量評估，引入了層次分析的方法，描述了該方法對問題的計算過程，其可以廣泛應用在資源分配、優(yōu)選排序、政策分析及決策預報等領(lǐng)域。

參考文獻

[1] 紀曉韻.大數(shù)據(jù)分析在高職教學質(zhì)量評估中的應用[J].科技創(chuàng)新導報，2019，16（13）：205-207，209.

[2] 姚兆，樸慧京，高飛.任職教育院校教學評估思考[J].科技資訊，2016，14（33）：105，107.

[3] 張俊婷.新時代高等院校教學質(zhì)量評價的創(chuàng)新探索[J].創(chuàng)新創(chuàng)業(yè)理論研究與實踐，2019，2（12）：37-38.

[4] 董國玉，祁迎春.層次分析法在高校課堂教學質(zhì)量評估中的應用研究[J].中國成人教育，2017（9）：53-56.

[5] 任雅楠.高職教學質(zhì)量評估系統(tǒng)的設(shè)計與實現(xiàn)[D].西安：西安電子科技大學，2017.

[6] 林光彬，洪煜.學生評教的行政化與學術(shù)化論析[J].教育研究，2016，37（8）：40-46.

[7] 胡昌送，高月勤，杜瑞軍.我國高校教師教學質(zhì)量評價的問題與對策[J].中國職業(yè)技術(shù)教育，2018（18）：80-84.

[8] 付沙，周航軍，肖葉枝，等.高校教師教學發(fā)展與評價體系探究[J].教育探索，2019（4）：92-95.