“函數(shù)單調(diào)性”概念建構(gòu)過程的教學(xué)反思與重構(gòu)

蔣智東　戈晨曦

[摘要]函數(shù)的性質(zhì)是函數(shù)知識的一個(gè)重要內(nèi)容.所有函數(shù)性質(zhì)學(xué)習(xí)活動(dòng)本質(zhì)是相同的，都是用抽象的代數(shù)式去刻畫函數(shù)圖像的幾何特征函數(shù)單調(diào)性”是函數(shù)的核心概念，在教學(xué)中具有引領(lǐng)作用，教師應(yīng)引起重視.

[關(guān)鍵詞]函數(shù)單調(diào)性;教學(xué);反思;重構(gòu)

[中圖分類號]G633.6? [文獻(xiàn)標(biāo)識碼]A? [文章編號]1674-6058（2020）02-0001-03

函數(shù)的性質(zhì)是函數(shù)知識的一個(gè)重要內(nèi)容.在高中階段，主要研究函數(shù)的單調(diào)性、奇偶性和周期性.所有函數(shù)性質(zhì)的學(xué)習(xí)活動(dòng)本質(zhì)是相同的，都是用抽象的代數(shù)式去刻畫函數(shù)圖像的幾何特征函數(shù)單調(diào)性”是蘇教版教材中代數(shù)模塊的一個(gè)核心概念，是函數(shù)性質(zhì)中第一個(gè)引人的概念，在教學(xué)中具有引領(lǐng)作用.

一、教學(xué)現(xiàn)狀與反思

在日常教學(xué)中，仍有許多教師為追求教學(xué)進(jìn)度和所謂的課堂容量，在進(jìn)行函數(shù)單調(diào)性教學(xué)時(shí)，快速引人函數(shù)單調(diào)性的概念，匆忙進(jìn)入函數(shù)單調(diào)性的判斷，并將學(xué)習(xí)的重點(diǎn)放在怎樣判斷函數(shù)在給定區(qū)間上的單調(diào)性上，然后基于若干個(gè)具體例子提煉函數(shù)單調(diào)性的判斷步驟，最后用精練的語言進(jìn)行概括，以方便學(xué)生記憶和運(yùn)用.

也有相當(dāng)一部分教師重視數(shù)學(xué)概念教學(xué)，重視概念教學(xué)中學(xué)生的概括、抽象等數(shù)學(xué)素養(yǎng)的培養(yǎng).但是，由于對數(shù)學(xué)概念教學(xué)和“函數(shù)單調(diào)性”概念理解上的差異，使得概念教學(xué)還存在許多值得改進(jìn)的地方.

其一，在“函數(shù)單調(diào)性”概念建構(gòu)的初始階段，學(xué)生需要通過實(shí)例來感悟函數(shù)圖像的“上升”和“下降”，提取函數(shù)的圖像特征.有的教師直接利用了教材上的“氣溫變化圖”，難免有片面性.因?yàn)椋瘮?shù)圖像的幾何形態(tài)是多樣的，在定義域上有上升的，有下降的，或在其定義域的某個(gè)區(qū)間上是上升的，在另一個(gè)區(qū)間上是下降的，等等.氣溫變化圖中只是其中一種情形，由于來自具體實(shí)際，又顯得過于復(fù)雜，這樣會(huì)阻礙甚至不能幫助學(xué)生從幾何直觀的角度形成對函數(shù)單調(diào)性的比較全面的認(rèn)識.這種缺失，會(huì)直接影響學(xué)生對函數(shù)單調(diào)區(qū)間的局域性以及單調(diào)區(qū)間與函數(shù)定義域之間的關(guān)系的認(rèn)識和正確理解.

其二，有的教師直接由“氣溫變化圖”出發(fā)引領(lǐng)學(xué)生經(jīng)歷函數(shù)單調(diào)性定義的形式化的形成過程，不符合學(xué)生的“認(rèn)知規(guī)律氣溫變化圖”實(shí)際上只是起到引入的作用.一是時(shí)間變化氣溫就變化，它是一個(gè)函數(shù);二是這個(gè)函數(shù)圖像有比較明顯的升高或下降的趨勢變化，便于學(xué)生觀察并體會(huì)到這個(gè)特征.由于氣溫變化圖與學(xué)生初中熟悉的函數(shù)圖像相比，明顯復(fù)雜得多，再加上缺少函數(shù)解析式，這種情況下，直接作為引例來探究函數(shù)單調(diào)性定義，可能會(huì)影響或弱化學(xué)生的探究意識和探究能力的培養(yǎng).

其三，學(xué)生在初中階段對函數(shù)單調(diào)性已經(jīng)有了初步的認(rèn)識，有的教師對高中階段函數(shù)單調(diào)性為什么要從研究圖像過渡到研究函數(shù)解析式，研究的必要性沒有做出交代，缺少一個(gè)邏輯上的銜接.

其四，引導(dǎo)學(xué)生經(jīng)歷一個(gè)掙脫“無限”桎梏的過程是“函數(shù)單調(diào)性”概念建構(gòu)的難點(diǎn).許多教師仍是心有余而力不足.由于設(shè)計(jì)不恰當(dāng)和引導(dǎo)不到位，對“增大”“隨”“任意”等關(guān)鍵字、詞還是做了正面的講解與引導(dǎo)，給出了函數(shù)單調(diào)性符號化的描述，探究合作的成分不多.

二、在實(shí)踐中重構(gòu)教學(xué)

數(shù)學(xué)概念有其發(fā)生、發(fā)展、形成和應(yīng)用的過程.在初中數(shù)學(xué)知識的基礎(chǔ)上，學(xué)生對函數(shù)單調(diào)性的認(rèn)識應(yīng)有三個(gè)階段.首先，借助函數(shù)圖像的幾何特征，從語言上對函數(shù)的單調(diào)性加以描述;其次，從圖像過渡到解析式，由感性認(rèn)識上升到理性認(rèn)識;最后，完成歸納，抽象出函數(shù)單調(diào)性的符號化定義.

為使學(xué)生充分感受數(shù)學(xué)概念的發(fā)生與發(fā)展過程，經(jīng)歷觀察、歸納、抽象的探究過程，加深對函數(shù)單調(diào)性的本質(zhì)的認(rèn)識，可以設(shè)計(jì)三個(gè)環(huán)節(jié)，引導(dǎo)學(xué)生分別完成對函數(shù)單調(diào)性定義的三次認(rèn)識（本文重點(diǎn)談前兩次認(rèn)識）.

[教學(xué)設(shè)計(jì)]

在情境教學(xué)階段，出示我市某天24小時(shí)內(nèi)的氣溫變化圖，引導(dǎo)學(xué)生識圖，捕捉信息，啟發(fā)學(xué)生思考.通過活動(dòng)，讓學(xué)生體會(huì)到函數(shù)值隨自變量的變化而變化.

引言：對于自變量變化時(shí)，函數(shù)值是變大還是變小，是函數(shù)的重要性質(zhì)，稱為函數(shù)的單調(diào)性.同學(xué)們在初中對函數(shù)的這種性質(zhì)就有了一定的認(rèn)識，但是沒有嚴(yán)格的定義.今天我們的首要任務(wù)就是建立函數(shù)單調(diào)性的嚴(yán)格定義.

1.借助圖像，直觀感知

本環(huán)節(jié)的教學(xué)主要是從學(xué)生的已有認(rèn)知出發(fā)，即從學(xué)生熟悉的常見的函數(shù)圖像出發(fā)，直觀感知函數(shù)的單調(diào)性，完成對函數(shù)單調(diào)性定義的第一次認(rèn)識.

問題1：分別作出函數(shù)y=x+2，y=-x+2，y=x²以及y=1/x的圖像，并且觀察自變量變化時(shí)，函數(shù)值有什么變化規(guī)律？

在學(xué)生畫圖的基礎(chǔ)上，引導(dǎo)學(xué)生觀察圖像，獲得信息：第一個(gè)圖像從左向右逐漸上升，y隨x的增大而增大;第二個(gè)圖像從左向右逐漸下降，y隨x的增大而減小.然后讓學(xué)生明確，自變量變化時(shí)，函數(shù)值具有這兩種變化規(guī)律的函數(shù)，我們分別稱為增函數(shù)和減函數(shù).

對兩個(gè)函數(shù)圖像的上升與下降要分段說明.通過討論，使學(xué)生明確函數(shù)的單調(diào)性是對定義域內(nèi)某個(gè)區(qū)間而言的，是函數(shù)的局部性質(zhì).

對于概念教學(xué)，若學(xué)生能用自己的語言來表述概念的相關(guān)屬性，則能更好地理解和掌握概念.

問題2：能否根據(jù)自己的理解說說什么是增函數(shù)，什么是減函數(shù).

引導(dǎo)學(xué)生進(jìn)行分類描述（增函數(shù)、減函數(shù)），并用自己的語言描述增函數(shù)的定義：

如果函數(shù)f（x）在某個(gè)區(qū)間上的圖像從左向右逐漸上升，或者如果函數(shù)f（x）在某個(gè)區(qū)間上隨自變量x的增大，y也越來越大，我們就說函數(shù)f（x）在該區(qū)間上為

增函數(shù).

然后讓學(xué)生類比描述減函數(shù)的定義.至此，學(xué)生對函數(shù)單調(diào)性就有了一個(gè)直觀、描述性的認(rèn)識.

2.探究規(guī)律，理性認(rèn)識

在此環(huán)節(jié)中，可以設(shè)計(jì)兩個(gè)問題，通過對兩個(gè)問題的研究、交流、討論，將函數(shù)的單調(diào)性研究從研究函數(shù)圖像過渡到研究函數(shù)的解析式，使學(xué)生對單調(diào)性的認(rèn)識由感性認(rèn)識上升到理性認(rèn)識，完成對概念的第二次認(rèn)識.

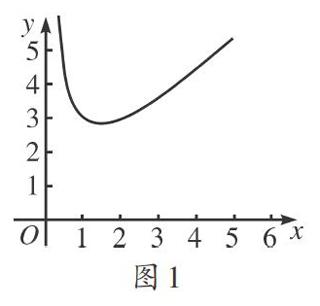
問題3：圖1是函數(shù)y=x+（2/x）（x>0）的圖像，能說出這個(gè)函數(shù)分別在哪個(gè)區(qū)間為增函數(shù)和減函數(shù)嗎？

學(xué)生解決問題所遇到的困難是難以確定分界點(diǎn)的確切位置.通過討論，使學(xué)生感受到用函數(shù)圖像判斷函數(shù)單調(diào)性雖然比較直觀，但有時(shí)不夠精確，需要結(jié)合解析式進(jìn)行嚴(yán)密化、精確化的研究;使學(xué)生體會(huì)到用數(shù)量大小關(guān)系嚴(yán)格表述函數(shù)單調(diào)性的必要性，從而將函數(shù)的單調(diào)性研究從研究函數(shù)圖像過渡到研究函數(shù)的解析式.

問題4：如何從解析式的角度說明f（x）=x²在[0，+∞）上為增函數(shù)？

在前面問題的鋪墊下，問題4是形成函數(shù)單調(diào)性概念的關(guān)鍵.在教學(xué)中，教師可組織學(xué)生先分組探究，然后全班交流，相互補(bǔ)充，并及時(shí)對學(xué)生的發(fā)言進(jìn)行反饋、評價(jià)，對于普遍出現(xiàn)的問題組織學(xué)生討論，使學(xué)生在辨析中達(dá)成共識.

[課堂實(shí)錄]

生1：只需用數(shù)學(xué)式子來描述：“在區(qū)間[0，+∞）上，當(dāng)自變量x增大時(shí)，函數(shù)值f（x）隨之增大.”

生2：“增大”意味著比較，需要建立兩個(gè)量的大小關(guān)系.

師：好！那應(yīng)該怎樣表示呢？

生3：在區(qū)間[0，+∞）內(nèi)取兩個(gè)數(shù)，比如2和3，因?yàn)?<3，且f（2）=42