初三數(shù)學復習課中的分層走班教學實踐探究

盛秀芬

(浙江嘉興海鹽縣濱海中學 浙江嘉興 314300)

傳統(tǒng)的班級上課制度有效率高、規(guī)模化的特點，但無法滿足不同水平、不同能力的學生的需求。這樣的現(xiàn)象在初中數(shù)學復習階段尤為明顯。而分層走班教學的出現(xiàn)，正好為解決這一問題提供了方法。

一、用愛心、耐心和細心感化學生，重樹他們學習的信心

“學困生”共同的弱點就是自卑感強，自我評價較低。因此，教師首先在思想上應重視他們，用耐心和細心幫助他們總結學習失敗的原因，消除其數(shù)學學習的畏懼心理。

二、復習中注重基本知識和規(guī)律

“學困生”對所學的知識點不能轉化成解題能力，不是因為對知識一點也不懂，而是理解得不夠全面，不夠透徹。因此，教師可以先通過練習了解學生對知識點的掌握情況，對學生學習中出現(xiàn)的錯誤和缺陷加以糾正并不斷訓練強化，對個別學生進行跟蹤輔導，在復習中補充適當?shù)木毩暎姑恳徊糠值膹土暥寄苓_到“知識點測試→信息反饋→矯正強化”這樣一個良性循環(huán)[1]。

三、復習中精講細練，由淺入深，循序漸進

“學困生”上課時注意力不太集中，特別是在上課的后半段時間容易走思。因此，教師在課前要精心設計復習內容，合理安排復習進度。課堂復習盡可能在前三十分鐘內解決重要內容，授課時言簡意賅、突出重點、分散難點、降低起點、減小坡度、避免要求過高。對于難點內容，要適當分解，多臺階、小步走，必要時應適當重復使其易被“學困生”接受，這樣有助于他們克服畏懼心理。

四、復習中創(chuàng)造學習氛圍，體驗成功，激發(fā)學習興趣

“學困生”一般學習興趣不濃， 學習信心不足。教師在復習中應充分考慮學生的實際，準確選好起點。在教學中創(chuàng)設各種環(huán)境，幫助他們克服困難，使他們能夠“跳起來摘蘋果”，從而獲得學習成功的快樂，從而樹立他們學習的信心。例如，上課中，教師的語氣應是輕松愉悅的；練習應該是基礎性較強的，可以選擇中考真題中較基礎的題目，適當增加一點點的挑戰(zhàn)性題目；有難度的題目，分步設疑，減小坡度；同時多多鼓勵，多多表揚。

五、復習中瞄準中考，強化雙基訓練，過好最后一關

一份嘉興中考數(shù)學試卷滿分為120分，基礎題占總分值的80%左右，即96分左右，這個分值對于“學困生”來說是可望而不可及，但若教師能有計劃、有目的、有針對性不斷強化雙基訓練，也是能達成的。針對上述情況，可采取如下措施：

第一，在單元知識復習中，平時多收集中考中常見知識點及相關的基礎題，強化訓練，熟悉中考。

第二，單元復習后，對中考基礎題型進行專題歸類，如倒數(shù)、相反數(shù)、絕對值的類型，分解因式的類型，自變量取值范圍的類型，求二次函數(shù)的頂點坐標的類型等，使他們對基礎題穩(wěn)操勝券。

第三，每個星期做一份中考綜合卷，使他們適應綜合性試卷。

通過這樣的設計，使他們感悟到中考題對他們來說并不是“洪水猛獸”。

在進行初三總復習“二次根式”的過程中，對于A班的學生，由于其自主學習能力強，有關分式知識的梳理回顧，放在課前的知識任務單中。在課堂教學中，將直接運用題目來回憶知識應用知識，深化知識。

如對于二次根式概念和性質知識這一部分知識點，可以如下設計：

對于B班學生，由于其自主性差，基礎薄弱，可由教師帶著學生運用題目回顧二次根式的相關知識點，并強化知識點的應用。如在二次根式的概念與性質的回顧中，可進行如下設計：

（讓學生理解掌握二次根式被開方數(shù)的非負性）

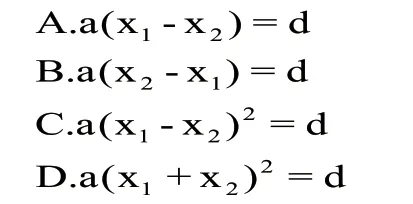
還是以獨立思考和組內合作討論為主要教學形式，同時關注解題速度，注重解題思想的運用，解題方法的多樣性。

對于B班學生，基于基礎薄弱、積極性較差的劣勢，以及課程標準的要求，在這一部分的復習中，重點是回顧一元二次方程的解法，可先出示以下方程：

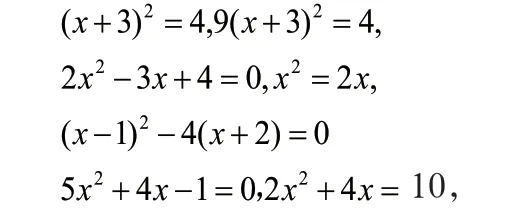
學生獨立完成，教師巡視，并作個別指導，解題后，用投影在全班展示解題優(yōu)秀的學生，關注解題方法的選擇，目的是先通過練習來了解學生對一元二次方程各種解法的掌握情況，并機動性地對學生不熟練的方法進行反復練習，并再次用中考真題中的一元二次方程題讓學生求解，成功后表揚學生。同時加大解方程難度，出示系數(shù)較為復雜的一元二次方程進行求解，中考中常常會出現(xiàn)系數(shù)復雜，但有技巧的解答方式的二次方程，因此方程的求解主要關注方法的選擇，對于方程求解非常困難的學生，選擇求根公式法較為合適。

函數(shù)是中學數(shù)學階段最難的，也是最為重要的知識。對于這部分內容的復習，需要一個循序漸進的過程。以二次函數(shù)解析式的求解為例。

A班的學生基礎相對扎實，對于函數(shù)的認識相對透徹。可以出示以下題目：

1.經(jīng)過A（4，0），B（-2，0），C（0，3）三點的拋物線表達式_______。

2.已知二次函數(shù)y=ax2+bx+c，自變量x與函數(shù)y的對應值如表：

?

求解二次函數(shù)表達式______________。

3.在體育測試時，初三的一名高個子男同學推鉛球，已知鉛球所經(jīng)過的路線是某個二次函數(shù)圖像的一部分，如圖所示，如果這個男同學的出手處A點的坐標為(0，2)，鉛球路線的最高處B點坐標為(6，5)(6，5)，求這個二次函數(shù)的解析式____________。

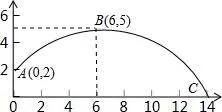
4.建立適當?shù)钠矫嬷苯亲鴺讼到鉀Q實際問題。

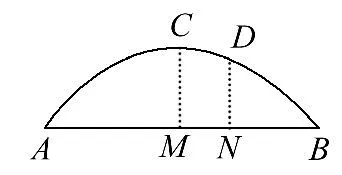
如圖，一石拱橋呈拋物線狀，已知石拱跨度AB為40m，拱高CM為16m，把橋拱看作一個二次函數(shù)的圖像，建立適當?shù)钠矫嬷苯亲鴺讼担蠖魏瘮?shù)的表達式__________。

對于B班的學生，函數(shù)的復習，應該耐心細致，肯花時間，循序漸進。從函數(shù)概念開始重新梳理一遍函數(shù)的知識，結合相關題目，讓學生對函數(shù)的認識能相比以往更加深入，多結合直觀的圖像解決抽象的函數(shù)問題，對函數(shù)解析式的求解也盡量以圖像為起點逐步擴散到文字型求解解析式。

特殊三角形相關知識的掌握對解決基礎幾何問題至關重要。以等腰三角形中考復習為例。除了要A班學生通過題目回憶等腰三角形相關概念，將著重發(fā)展與等腰三角形問題解決有關的分類討論能力以及計算相關邊角能力等。可以讓學生解決以下幾個題目：

1.等腰三角形的周長為22cm，其中一邊的長是8cm，則其余兩邊長分別為_________。

2.在直角坐標系中，O點為坐標原點，A(2，-4)，動點B在坐標軸上。則滿足△OAB為等腰三角形的有B點共有________個。

對于B班學生，要求其掌握最基本的等腰三角形的概念，以及最基本的分類討論即可。同時，在分類討論中，注意強調前提是三角形三邊關系，三角關系的符合。

六、分層走班的實施原則

（一）走班的時機

分層走班可以是初三復習的開始，也可以進行一輪基礎復習后再分班。

（二）走班的發(fā)展性

經(jīng)過第一個學期的一個月或者期中考試，期末考試，學生可自主選擇留在哪個教學班級，教師也需要作好充分的引導。

從長時間的實踐來看，分層走班對全面提高教學質量，提高學生數(shù)學成績有顯著的幫助，雖然在實踐過程中遇到了一些困難，做得也有不到位的地方，但相信在未來，分層走班將是教學的一種發(fā)展趨勢。