超聲波電動機二輸入Hammerstein非線性建模

黃文文，宋 璐，史敬灼

(河南科技大學 電氣工程學院，洛陽 471023)

0 引 言

適合于控制應用的超聲波電動機數學模型，是超聲波電動機伺服控制系統設計與分析的必要基礎。為滿足不斷提高的控制性能要求，需要更好表述超聲波電動機運行特征的數學模型作為支撐。超聲波電動機內部機電能量轉換過程所具有的本質非線性，采用適當形式的非線性模型進行超聲波電動機系統建模，有可能得到更高精度的模型。

Hammerstein模型是眾多非線性模型形式中較為常用的一種。文獻[1-7]嘗試建立超聲波電動機Hammerstein模型，表明這種非線性模型形式適用于表述超聲波電動機系統的運行過程。文獻[1-5]直接將模型中的動態線性環節設定為一階慣性環節，這顯然不足以表述超聲波電動機的動態運行過程。文獻[6-7]采用不同的優化算法進行辨識建模，分別建立了用于轉速、位置控制的超聲波電動機Hammerstein模型，所建模型的非線性環節均采用傳統的多項式形式，受限于多項式的項數及具體建模方法，可能降低模型對電動機非線性特性的表述精度。

本文以電動機驅動電壓的幅值(峰峰值)和頻率為輸入變量，轉速為輸出變量，基于實測數據，采用改進差分進化算法建立超聲波電動機Hammerstein非線性模型。模型計算數據與實測數據的對比表明，所建模型精度較高。

1 實驗數據測試與預處理

為進行辨識建模，首先需要測取能夠反映超聲波電動機驅動電壓幅值、頻率與轉速之間特性關系的實驗數據。實驗用超聲波電動機為Shinsei USR60型超聲波電動機，驅動主電路為H橋結構，采用相移PWM控制方式和PI轉速控制器，同時包含兩相驅動電壓幅值的閉環控制以使其為期望值，并設定兩相驅動電壓之間的相位差為固定的90°。

分別設定驅動電壓幅值(峰峰值)給定值為240 V，260 V，280 V，300 V，320 V，在電動機允許的調速范圍0～120 r/min內，間隔10 r/min設定轉速階躍給定值，測取不同驅動電壓情況下的轉速階躍響應實驗數據。通過上述實驗，得到51組實測階躍響應數據用于辨識建模。另外，在轉速階躍給定值分別為30 r/min，60 r/min，90 r/min，120 r/min的情況下，各設置兩組不同于前述實驗的PI控制參數取值，進行階躍響應實驗，得到8組階躍響應數據用于模型校驗。

提取每組階躍響應實驗數據中的動態響應數據，用于Hammerstein模型動態線性環節的建模。同時，求取各組剩余的穩態數據的頻率、轉速平均值，如圖1中方形點所示。

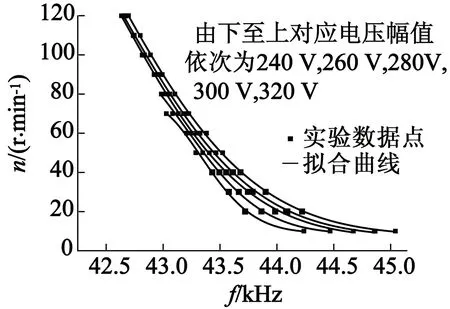
圖1 穩定實驗數據的擬合

2 模型靜態非線性環節表達式的確定

圖1給出了對應不同驅動電壓值的穩態頻率-轉速實驗數據，這些數據反映了超聲波電動機驅動電壓幅值、頻率與轉速之間非線性關系的主要方面，可用作建立Hammerstein模型靜態非線性環節的主要依據。下面嘗試分別對各個驅動電壓值情況下的“頻率-轉速”關系數據進行一輸入一輸出的函數擬合，研究不同驅動電壓值的擬合函數之間的相似性與差異，探究以驅動電壓幅值和頻率為輸入的“二輸入一輸出”非線性函數的恰當形式。

對不同擬合函數形式的嘗試表明，采用Gauss函數，不同電壓幅值的數據均能實現良好擬合，擬合曲線如圖1所示。所得擬合表達式分別如下：

240 V：x=9.050 9+65.077e-2.318 7(u-42.864)2(1)

260 V：x=8.462 6+88.651e-1.124 6(u-42.537)2(2)

280 V：x=6.435 9+185.79e-0.429 58(u-41.561)2(3)

300 V：x=7.077 8+188.34e-0.395 91(u-41.514)2(4)

320 V：x=7.582 5+216.46e-0.326 71(u-41.279)2(5)

式中:x為圖1穩態轉速值，此處亦為模型靜態非線性環節的輸出變量；u為電動機的驅動頻率，是模型靜態非線性環節的一個輸入變量。

為得到適用于不同驅動電壓情況的統一表達式，將上述擬合函數式(1)～式(5)寫為一般形式：

x=r1+r2er3(u-r4)2

(6)

式中：r1，r2，r3，r4為系數。

對比式(1)～(5)可知，不同驅動電壓情況下的r1，r2，r3，r4值各不相同。下面以驅動電壓值為自變量，分別對式(1)～式(5)中的r1，r2，r3，r4值進行擬合，得各系數擬合表達式：

(7)

(8)

(9)

(10)

至此，得到以驅動電壓幅值、頻率為自變量的Hammerstein模型靜態非線性環節為式(6)，式中系數采用式(7)～式(10)計算。

3 確定優化算法參數

采用改進的差分進化算法，對模型動態線性環節式(11)中的未知參數a1,a2,…,ana,b1,b2,…,bnb進行辨識，得到使目標函數值最小的模型參數值，即完成了建模。

(11)

式中：a1,a2,…,ana,b0,b1,…,bnb為待定系數，由辨識確定；na和nb為模型階次。

取如下均方差函數為表征模型與實驗數據之間差異大小的目標函數：

(12)

式中：m為建模數據的組數；h為每組建模數據的數據點數；y為模型計算值；ye為實測值。

模型辨識所用改進差分進化算法與標準差分進化算法的區別在于，改進變異操作如式(13)，并引入自適應變異算子F和F2，使優化進程中側重于全局搜索還是局部搜索變為可控可調。

Vi(t+1)=Xi(t)+F[Xbest(t)-Xi(t)]+

F2[Xr1(t)-Xr2(t)]

(13)

式中：r1,r2∈{1,2,3,…,Np}為隨機選取的互不相同的數，且均與i不同；Np為初始種群個體數量；Xi(t)為第t代種群中的目標個體矢量；Vi(t+1)為目標矢量所對應的變異個體矢量；Xbest(t)為第t代種群中的最優個體矢量。

優化算法參數的取值是否合適，直接決定了能否得到準確的辨識結果。在差分進化算法中，需要確定的算法參數包括Np、變異算子F和F2、交叉算子CR、模型參數初始值上下限maxbound及minbound、最大迭代次數Gm等。其中，最大迭代次數用作優化計算的終止條件。算法參數選擇過程中，為避免隨機產生的不同初始種群影響算法參數對比結果，不同算法參數值的辨識過程都采用同一初始種群。以“na=4,nb=1”為例，通過嘗試不同參數值進行優化辨識，以最優目標值小、迭代用時少為依據，確定適合于本文建模問題的優化算法參數值：Np=50，maxbound=1，minbound=-1，Gm=100，CR=0.95，F2=0.55，并設置變異算子F：

(14)

4 確定模型階次

在合理范圍內，設定不同的模型階次，利用改進差分進化算法進行模型參數辨識，并采用校驗數據對辨識所得模型進行校驗。經模型參數辨識，得到優化建模與校驗結果如表1所示。 優化所得最優目標函數值和校驗目標函數值分別除以各自數據組數并求和，得到表1所示綜合誤差，以此作為確定模型階次的依據。考慮電動機實測階躍響應曲線的表征及控制性能要求，在3到4階之間選擇模型階次。

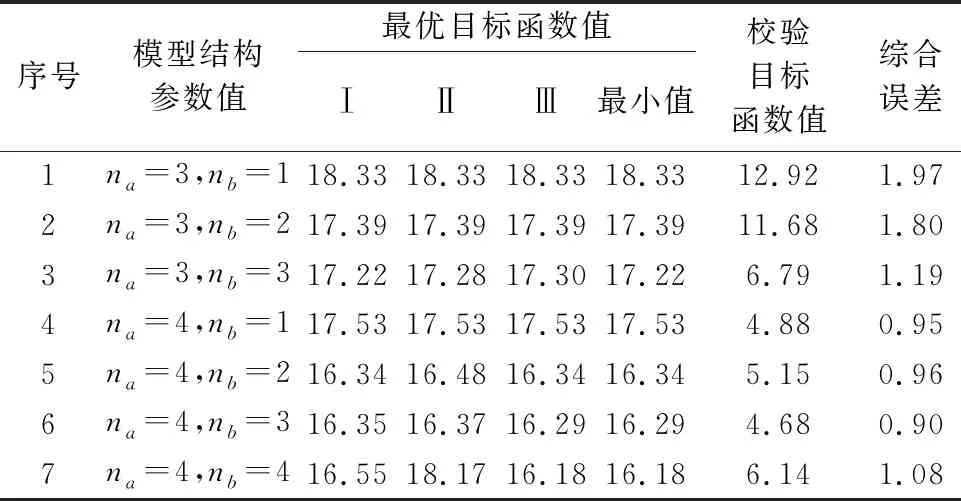
表1 不同模型階次情況下的優化結果和校驗結果對比

對比表1數據可知，第6組模型階次所得綜合誤差值最小，但第6組三次優化進程所得最優目標函數值存在明顯差異，優化進程表現不夠穩健。前述優化算法參數的確定過程，是在設定模型階次為na=4，nb=1的情況下進行的。表1中，第1、2和4組三次所得最優目標函數值都相同，而其它組三次所得最優目標函數值都存在差異，因為這些組需辨識的模型參數個數均大于na=4，nb=1的情況，優化問題的復雜度增加了。由此可知，在問題復雜度增加的情況下，需調整優化參數值，以保證算法的穩健性。

模型階次越高，所需辨識的模型參數個數越多，可行解空間維數越高，復雜度越高。對于差分進化算法而言，可按照下列原則來調整參數以保證找到最優解，一是調整變異算子值，加強全局搜索；二是增大初始種群數量，借助算法的隨機性質，可擴大搜索范圍；三是增大迭代次數。這是因為，在其它參數不變的情況下，問題復雜度增加，則最優目標函數值下降速度將減慢，算法需更多次迭代才能達到最優解。增大迭代次數將增加優化時間，同時可能因變異算子值不合適而得不到全局最優解，故應首先考慮加強全局搜索和增大初始種群數量。

表1數據表明，模型階次為na=4，nb=3時，綜合誤差值較小，更適合于本文所述超聲波電動機，故設定na=4，nb=3，調整變異算子值。加強全局搜索，可通過增大F2值或減小F值來實現。不同算法參數值嘗試過程表明問題復雜度增加，可通過加強全局搜索和初始種群數量來提高優化算法的穩健性，確定將初始種群數量和變異算子值調整為Np=100，F2=0.55，并減小變異算子F：

(15)

采用調整后的參數值，嘗試不同的模型階次，得到優化辨識結果如表2所示。觀察表2數據可知，調整參數值后，不同模型階次情況下，三次優化結果都各自相同，且三次辨識所得模型參數值相同，算法穩健性提高。根據表2的綜合誤差值，選定超聲波電動機Hammerstein模型動態線性環節的模型階次為na=4，nb=3，表達式：

(16)

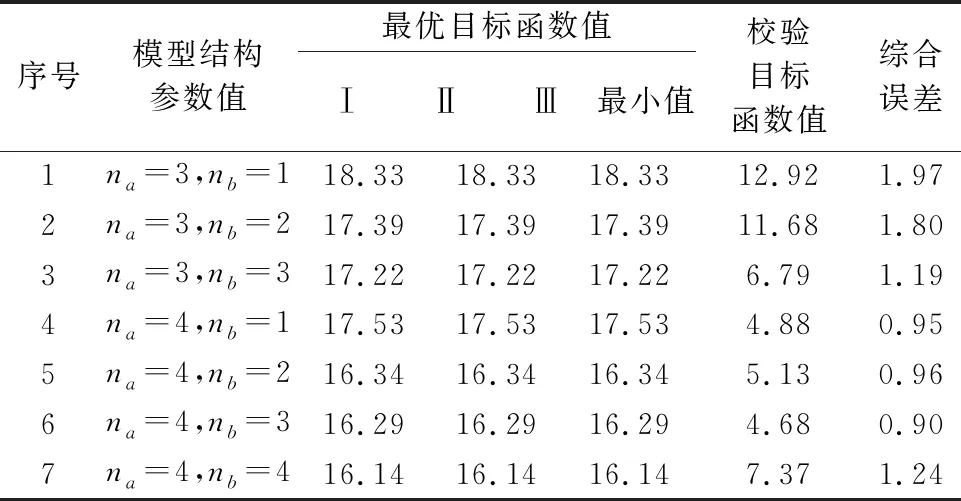
表2 不同模型結構下的優化結果對比

為驗證所建模型的準確度，將本文模型與文獻[6]所建超聲波電動機二輸入一輸出Hammerstein非線性模型進行對比。圖2、圖3給出了兩種模型的模型計算數據與實測電動機階躍響應數據的對比圖，可以看出，本文模型計算數據更接近實驗數據。對于51組建模數據，使用式(12)計算得到本文模型的計算輸出與實驗數據之間的總均方差值為16.29；采用8組校驗數據進行比對，對應的總均方差值為4.68。而文獻[6]模型的上述兩個總均方差值依次為574.86和109.76，可見本文所建模型精度明顯高于文獻[6]模型。

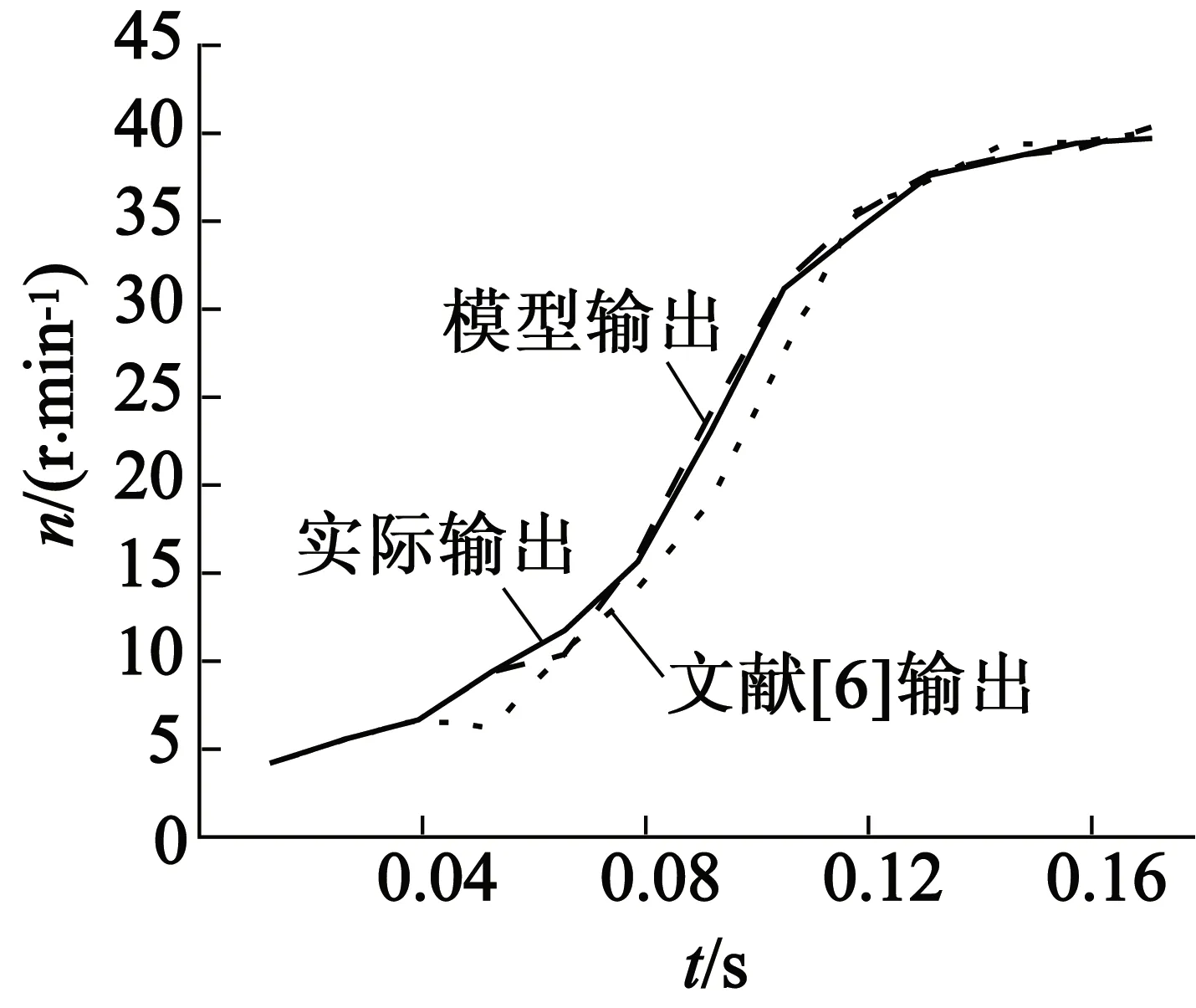
(a) U=240 V

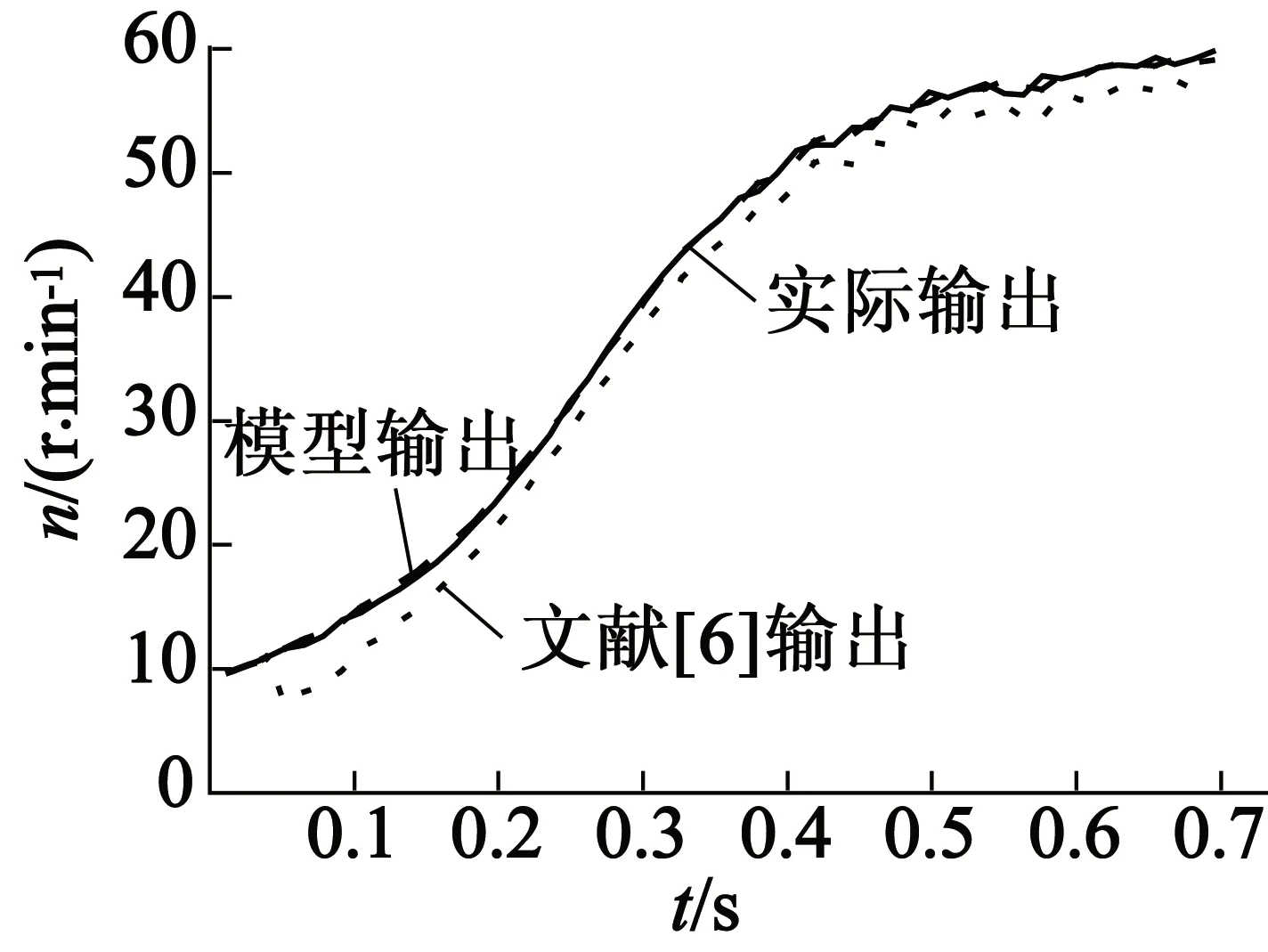
(b) U=300 V

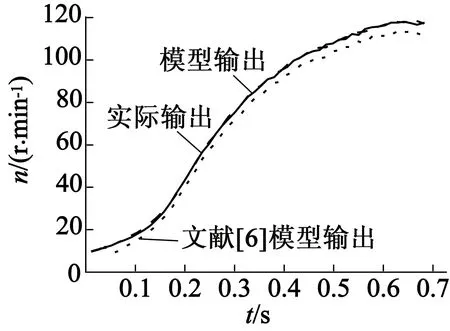
圖3 轉速階躍響應的校驗數據對比(120 r/min)

5 結 語

為給超聲波電動機控制系統的設計與分析提供必要基礎，采用改進差分進化算法進行辨識建模，建立以驅動電壓幅值(峰峰值)和頻率為輸入變量、電動機轉速為輸出變量的超聲波電動機二輸入一輸出Hammerstein非線性模型。基于實驗數據分析，模型靜態非線性環節設計為Gauss函數，函數中各系數為關于驅動電壓幅值的多項式，以求更準確地表述超聲波電動機的實際非線性特性。模型計算結果與實驗數據的對比表明，所建模型精度較高，建模方法有效。同時，給出了改進差分進化算法參數的調整原則，以提高優化算法的穩健性，保證建模過程的有效性并提高建模效率。

非線性模型建模方法與優化算法參數調整原則，不僅適用于超聲波電動機，也適用于其它種類電動機的建模。