基于MRAS的異步電機無速度傳感器應用研究

包廣清，祁武剛

(蘭州理工大學 電氣工程與信息工程學院，蘭州 730050)

0 引 言

在自動化裝配領域中，工業機械臂是最常見的形式。異步電機無速度傳感器矢量控制技術由于成本低、可靠性高的特點,被廣泛應用于機器人的關節驅動控制系統中。目前，已經有多種方法實現了對異步電機的速度辨識，如擴展Kalman[1-2]、線性矩陣不等法[3]、滑模觀測器[4]、全階觀測器[5]和模型參考自適應法[6]等。

模型參考自適應(以下簡稱MRAS)由于算法簡單、穩態精度較高已被廣泛應用于電機的控制，但仍存在一定的缺陷。

基于轉子磁鏈模型的MRAS觀測器，在低速時檢測精度差，且存在積分誤差和誤差積累的問題[7]；文獻[8]將無功功率與MRAS相結合，收斂速度較快，魯棒性也有所提高，但未考慮電機參數變化時的轉速辨識問題；文獻[9]利用反電動勢的MRAS轉速觀測器，成功地避開了純積分的問題，但是此方法在低速時估計值誤差值較大；文獻[10]將滑模控制策略作為MRAS結構中的自適應機制，但電壓參考模型中依然存在純積分的問題；文獻[11]采用一種可以同時進行轉速和定子電阻辨識的雙參數的MRAS模型，此方法對電機的定子電阻辨識度較高，卻增加了系統的復雜性；文獻[13]提出以模糊邏輯作為MRAS結構中的PI自適應率，此方法改善了傳統PI參數不能在線更新的問題，卻忽略了電壓參考模型中的積分問題。

本文在基于轉子磁鏈模型的MRAS速度觀測器的基礎上，采用一階慣性環節代替電壓模型中的純積分環節，以消除積分直流偏置的問題，同時設計了一種自適應線性(以下簡稱ADALINE)神經元PID控制器，ADALINE可以根據電機磁鏈、轉速的變化情況對自身的參數進行在線權值修正，該控制器改善了傳統的PI控制器不能根據電機的實際情況進行在線參數修正的問題，提高了速度觀測的精度。仿真結果驗證了該算法的可行性。

1 異步電機數學模型

三相異步電機在兩相靜止坐標系α，β下的電壓方程：

(1)

式中：usα，usβ為定子繞組電壓在α，β軸分量；urα，urβ為轉子繞組電壓在α，β軸分量；isα，isβ為定子繞組電流在α，β軸分量；irα，irβ為轉子繞組電流在α，β軸分量；ψsα，ψsβ為定子繞組磁鏈在α，β軸分量；ψrα，ψrβ為轉子繞組磁鏈在α，β軸分量；Rs,Rr為定、轉子單相繞組電阻；ω為轉子角速度。

磁鏈方程：

(2)

式中：Ls,Lr為α,β坐標系上定、轉子繞組自感；Lm為α,β坐標系上同軸定、轉子繞組間的互感。

轉矩方程：

Te=pLm(isβirβ-isαirβ)

(3)

式中：Te為電磁轉矩；p為異步電動機的極對數。

運動方程：

(4)

式中：J為機組的轉動慣量；TL為包括摩擦阻轉矩的負載轉矩。

2 無速度傳感器的速度觀測模型

2.1 MRAS速度觀測器的原理

轉子磁鏈觀測器有兩種不同的模型：電壓模型和電流模型。

電壓模型：

(5)

電流模型：

(6)

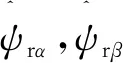
由式(5)和式(6)可知，ω是待辨識的參數。如圖1所示的速度辨識系統中，可調模型和參考模型分別為轉子磁鏈的電流模型和電壓模型。

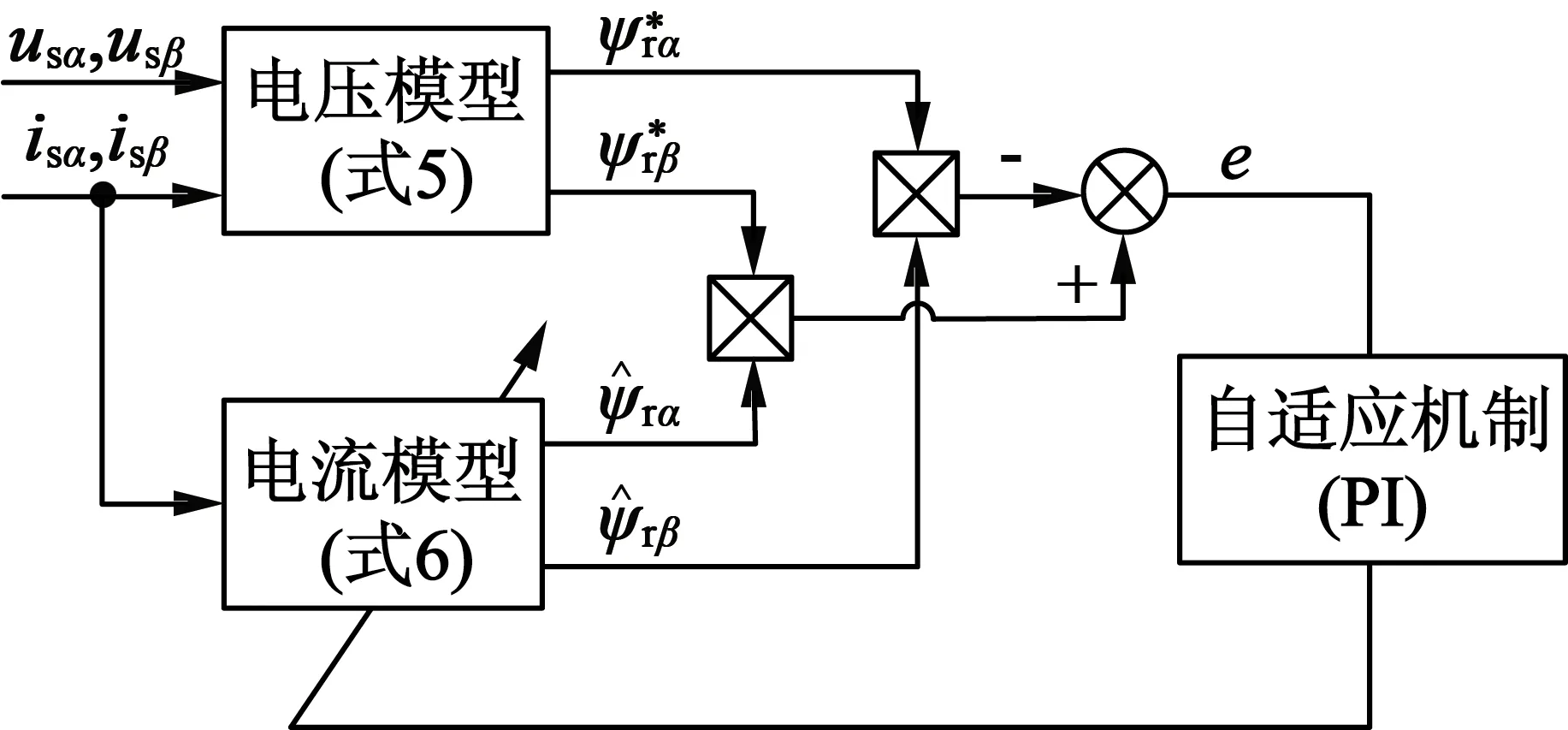
圖1 MRAS速度辨識框圖

根據Popov超穩性定律，該MRAS系統是漸進穩定的。在圖1中取廣義誤差e作為MRAS自適應律的輸入值,定義廣義誤差e：

(7)

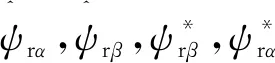
以PI為MRAS自適應率，計算電動機轉速ωr：

(8)

式中：KP為比例系數；KI為積分系數。

2.2 改進的MRAS轉速估算方法

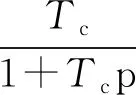
轉子的反電動勢：

(9)

轉子磁鏈估計的動態方程：

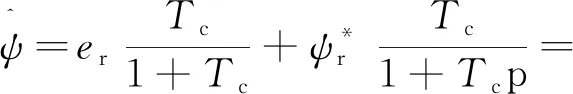
(10)

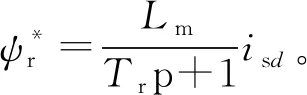
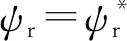
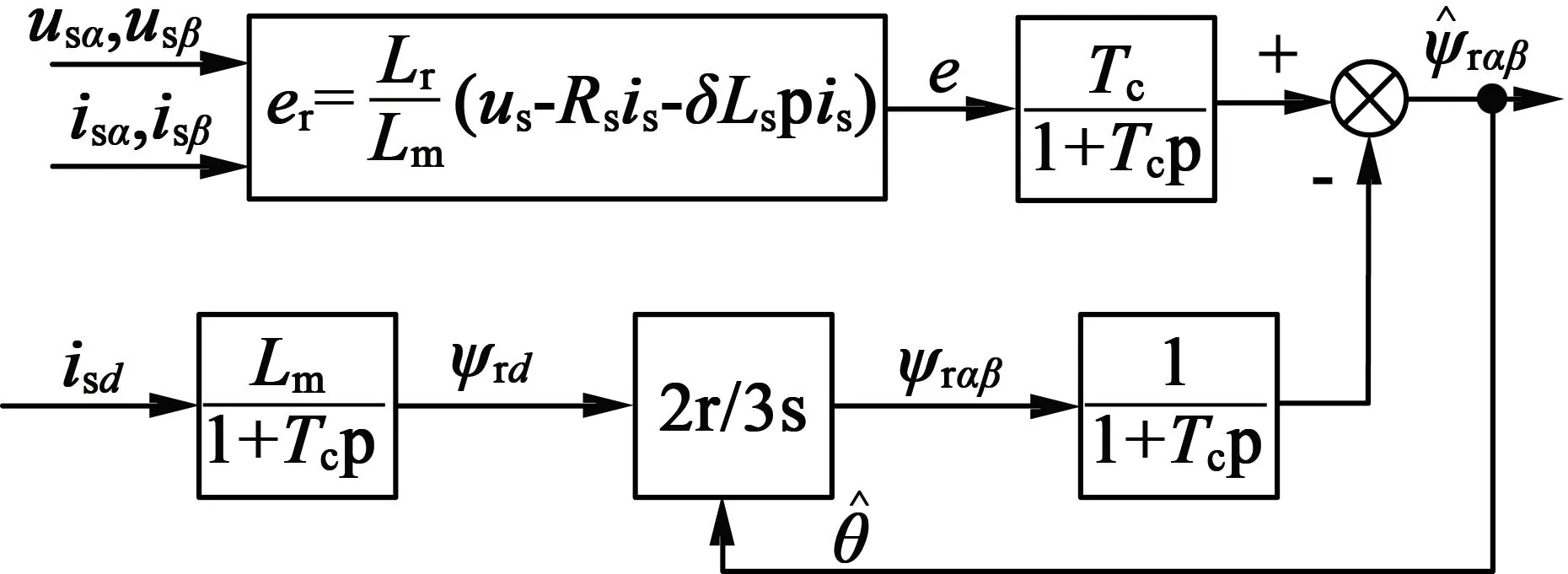
圖2 改進后的電壓模型原理圖

2.3 基于ADALINE的并聯雙模型速度辨識

傳統的基于轉子磁鏈的MRAS轉速辨識方法中，PI調節器不能根據電機磁鏈、轉速的變化進行在線修正，因此其誤差較大。本文將ADALINE作為MRAS的自適應機構，其權重參數在線修正，所以使得速度觀測更加準確。

由式(7)，采用PI調節器對磁鏈的廣義誤差進行處理，但PI參數的選取受制于異步電機的數學模型，事先選取適合的PI參數存在一定的困難。而ADALINE可根據外界的輸入和期望響應，其權值進行動態的調整，因此采用ADALINE代替傳統MRAS中的PI自適應率。ADALINE模型如圖3所示。

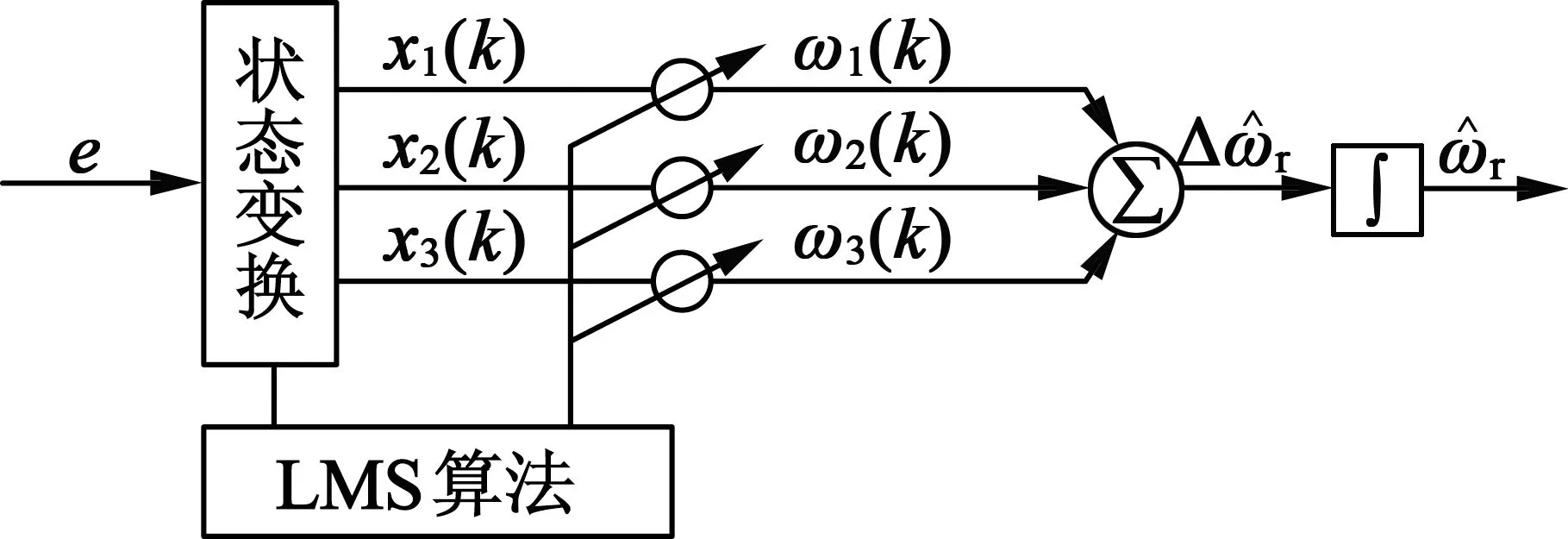
圖3 ADALINE結構模型

圖3中：x1(k),x2(k)和x3(k)為輸入信號；ω1(k),ω2(k),ω3(k)輸入信號的權重。根據轉子的廣義誤差e，定義狀態變量：

(11)

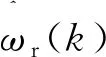
(12)

為了保證系統的收斂性，采用最小均方誤差算法(以下簡稱LMS)來修正ADALINE的加權系數。定義目標函數：

(13)

LMS算法是一種特殊的梯度估計算法，其權重系數采用反梯度向量進行反復迭代更新。根據梯度法，其權值系數的修正公式如下:

(14)

將式(12)和式(13)代入求偏導，可得：

(15)

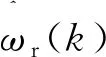
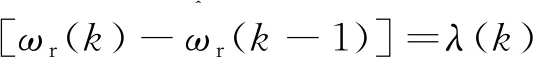
(16)

結合式(11)、式(14)、式(15)、式(16)，得到速度觀測器中權值自學習的差分表達式：

(17)

根據每次轉子磁鏈估計誤差計算此時的狀態變量，由式(17)進行權值更新，由式(11)得到電機的轉速估計。

3 仿真與結果分析

改進后的MRAS速度觀測器的控制系統如圖4所示，并在MATLAB/Simulink環境下對此控制模型進行仿真分析。

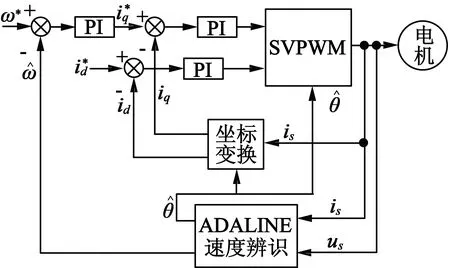
圖4 基于改進的MRAS速度觀測器控制框圖

電機的仿真參數如表1所示。

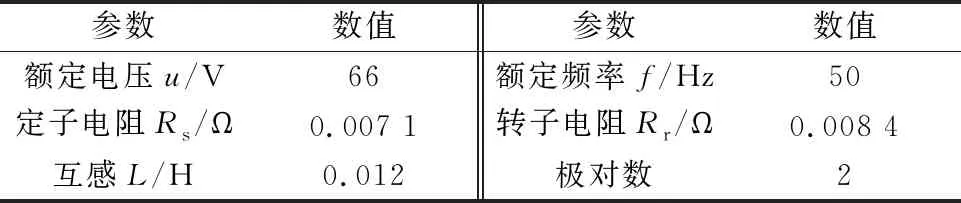
表1 電機的參數

電機給定轉速為1 000 r/min,空載起動，0.08 s時轉速上升至2 200 r/min，仿真結果如圖5所示。圖5(a)為電機定子間的線電壓;圖5(b)為轉速辨識與電機實測轉速的仿真圖，從圖5(b)中可知，辨識轉速的波動較小，較好地跟隨電機的實際轉速；圖5(c)為轉速的誤差圖，由圖5(c)可知，電機的在穩態時誤差很小，響應速度快；圖5(d)為電機的輸出轉矩；圖5(e)為定子電流；圖5(f)為轉子磁鏈運行軌跡圖。

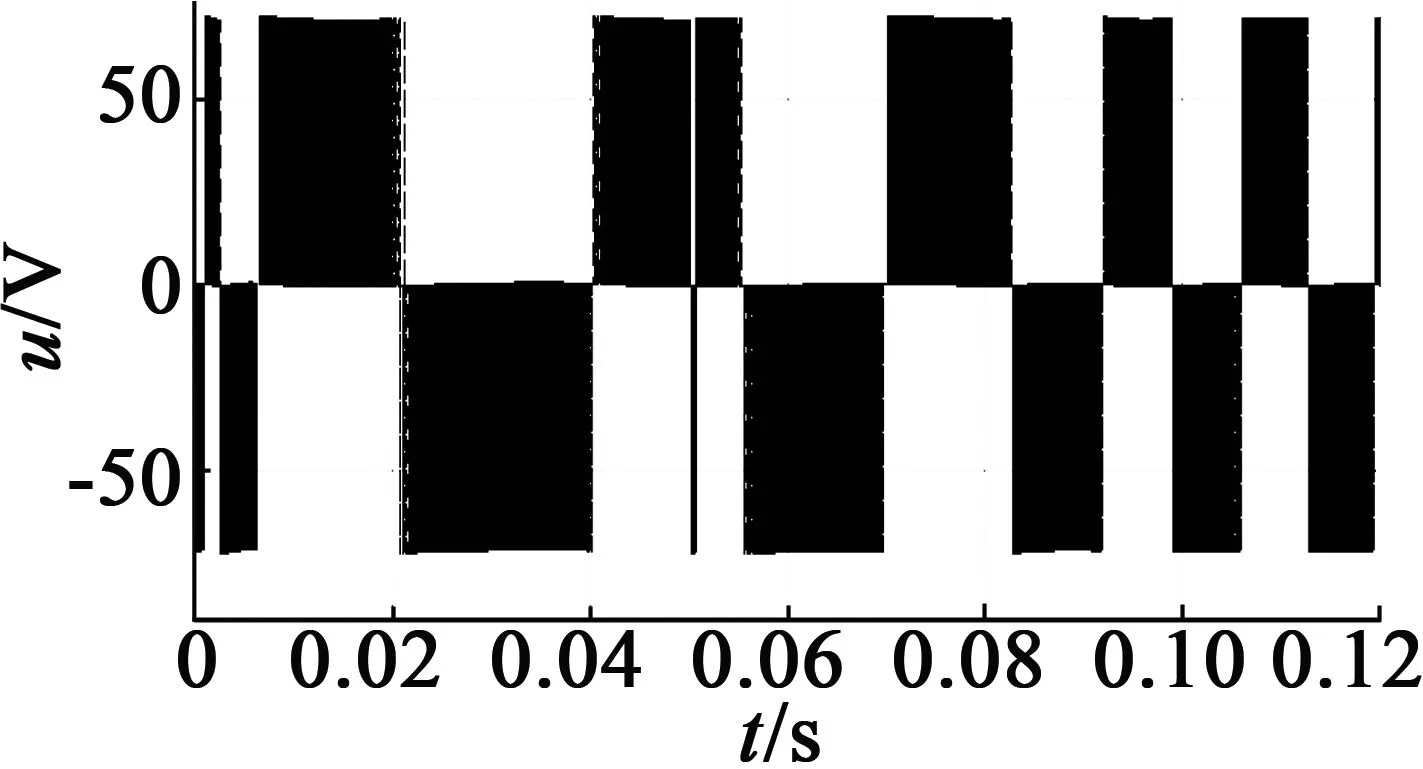
(a) 定子線電壓

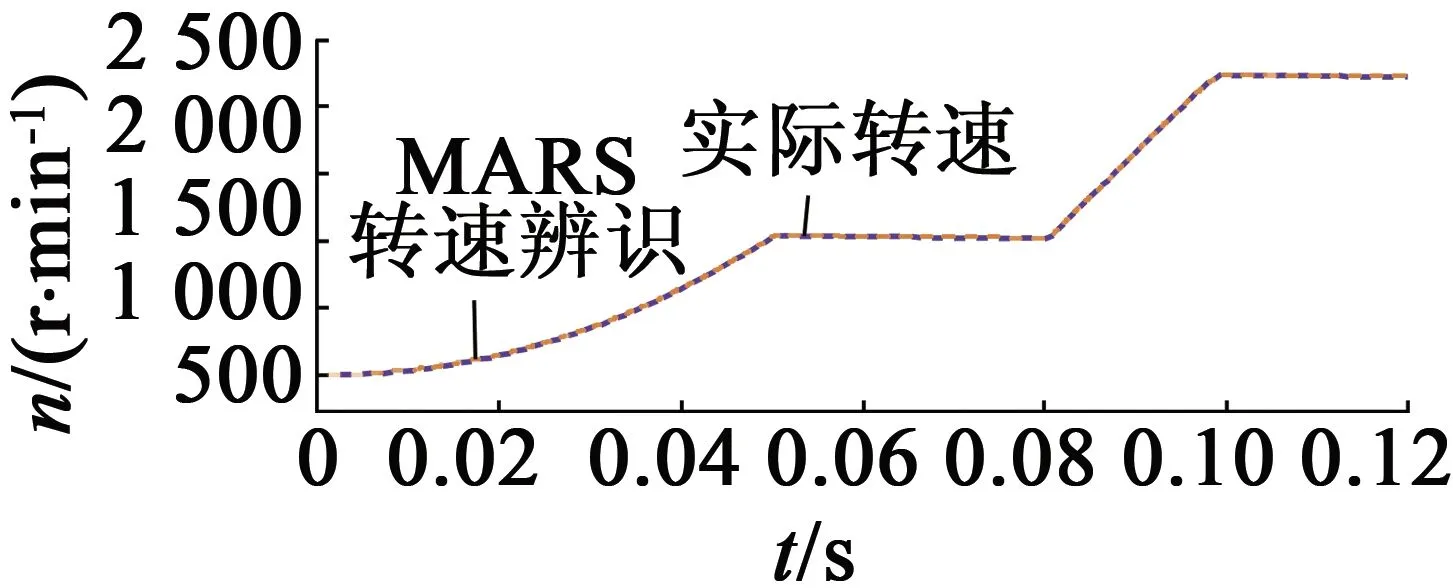
(b) 轉速響應

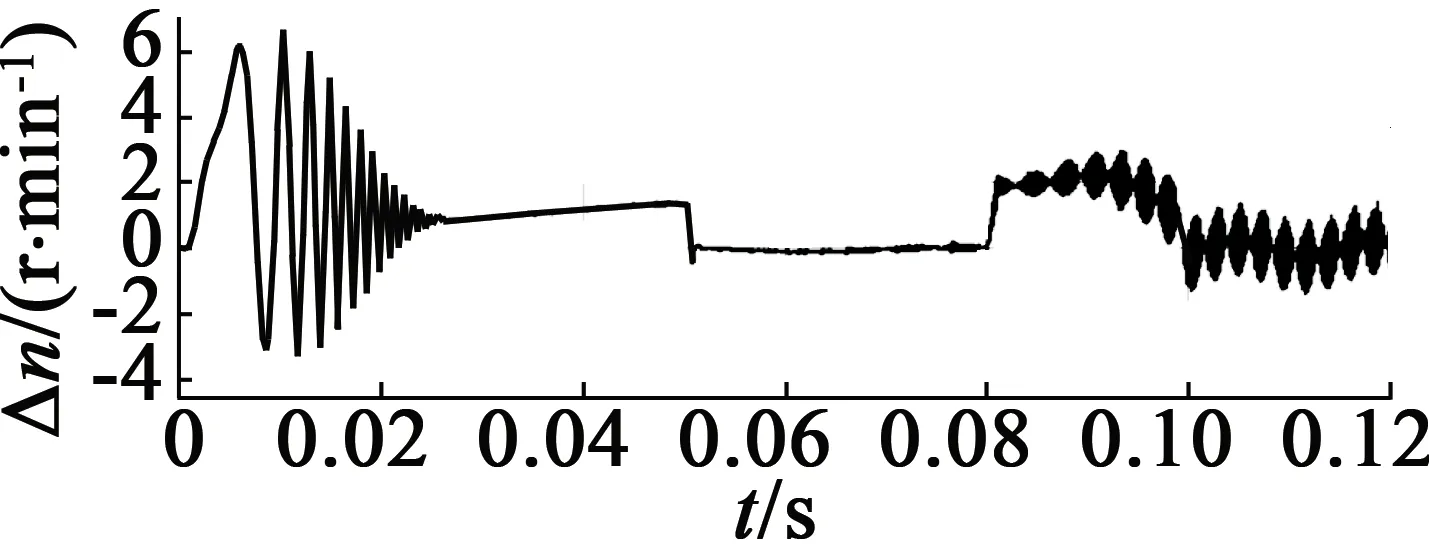
(c) 轉速誤差

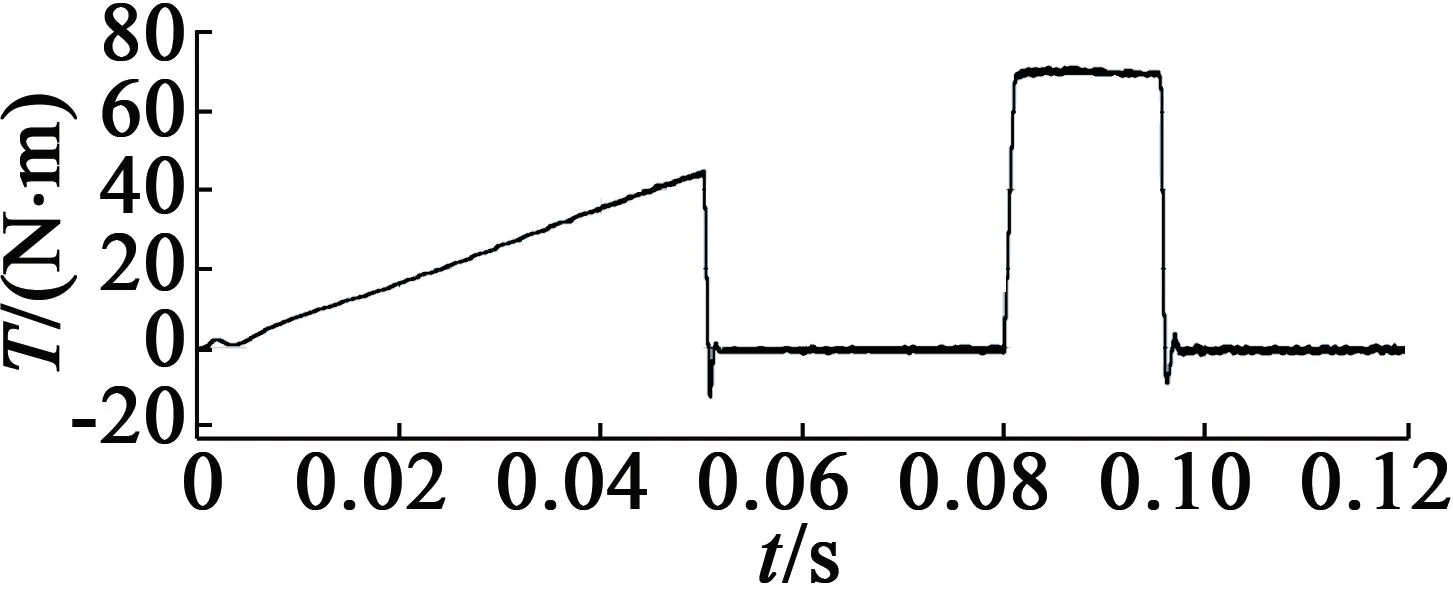
(d) 電磁轉矩

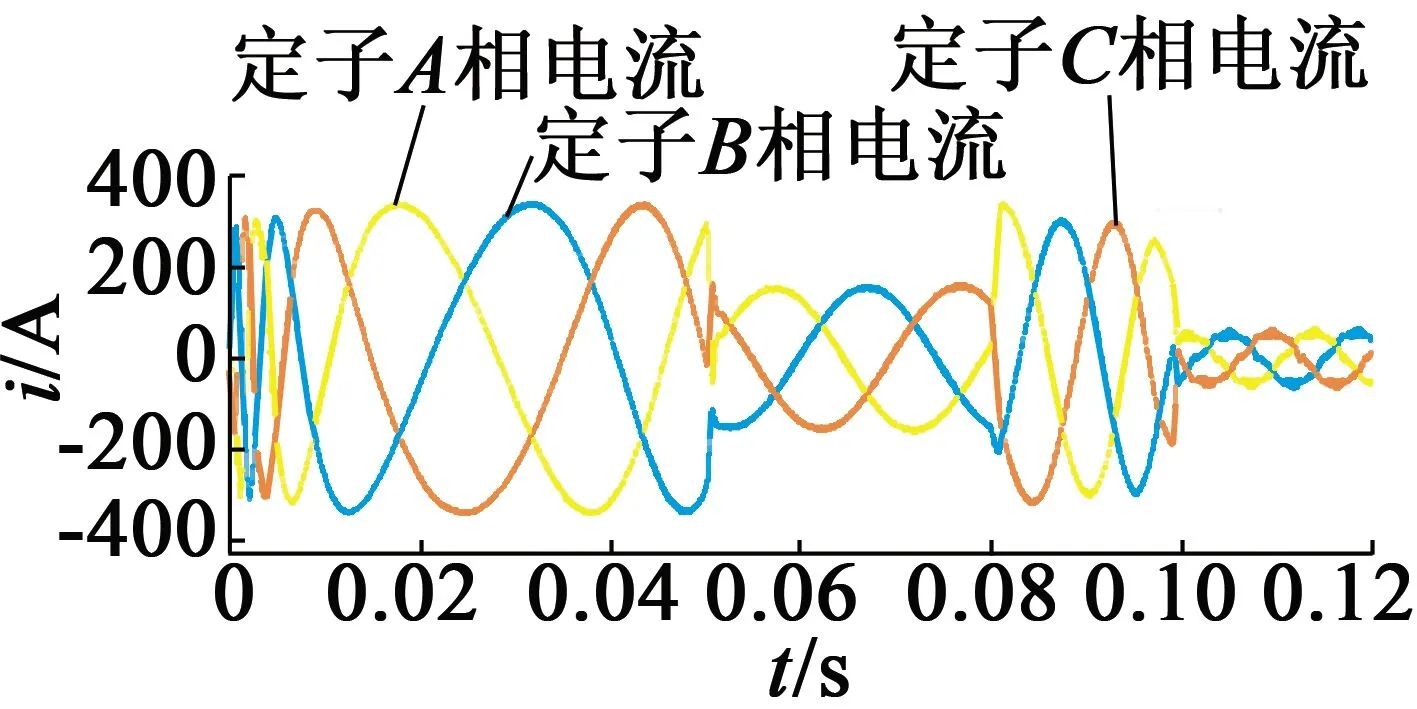
(e) 定子電流

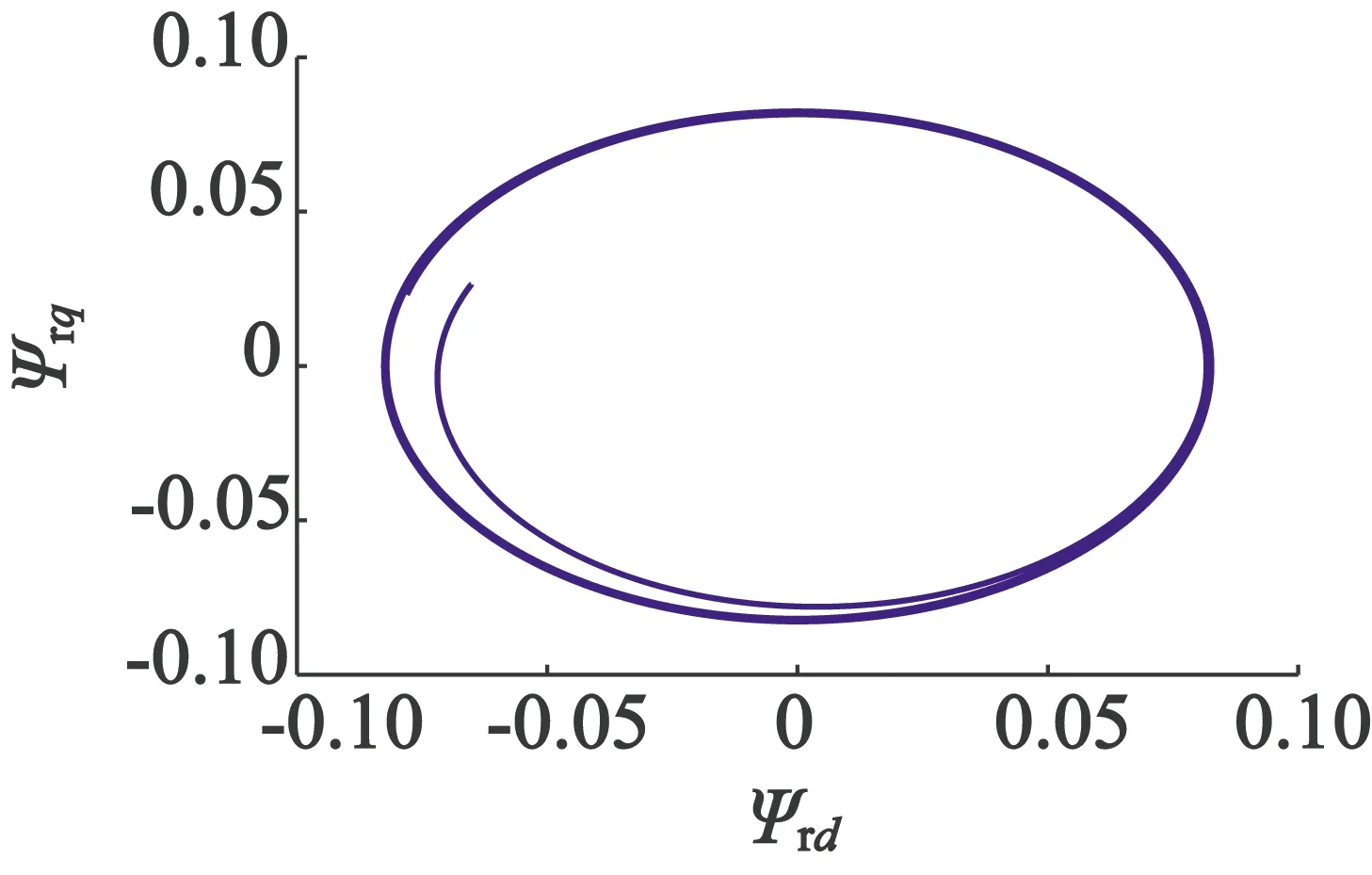
(f) 轉子磁鏈

圖6給定電機轉速為1 000 r/min,在0.06 s突加負載20 N·m，0.08 s時負載減至10 N·m的仿真結果。從圖6中可知,突加負載后轉速略有下降，但立即恢復。

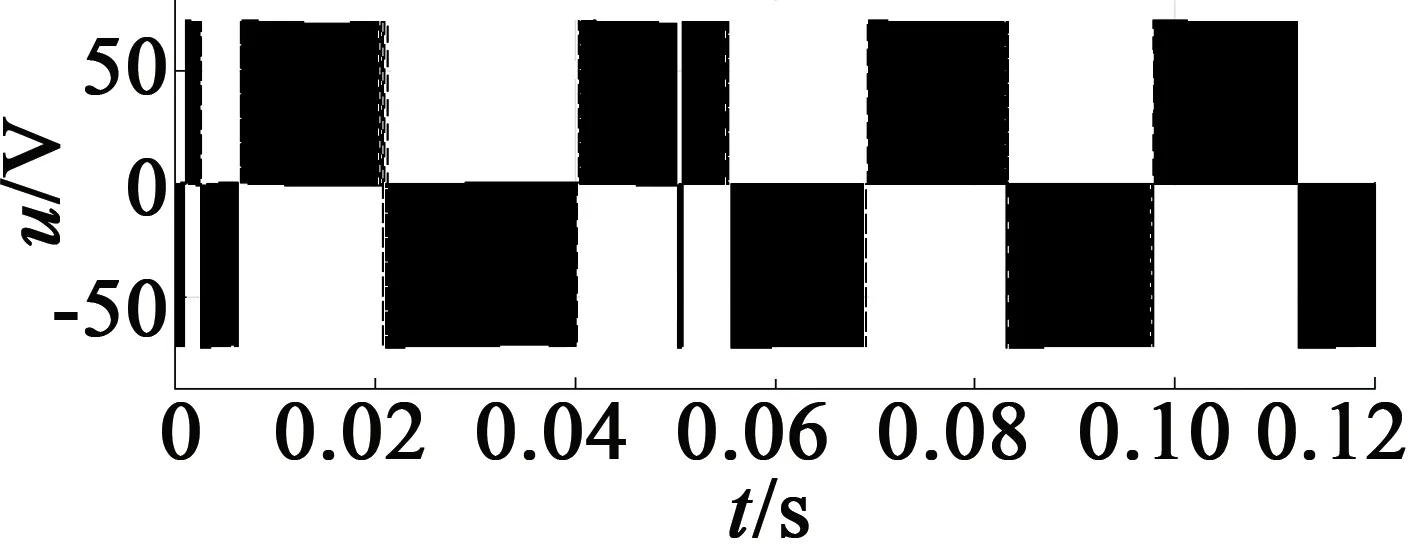
(a) 定子線電壓

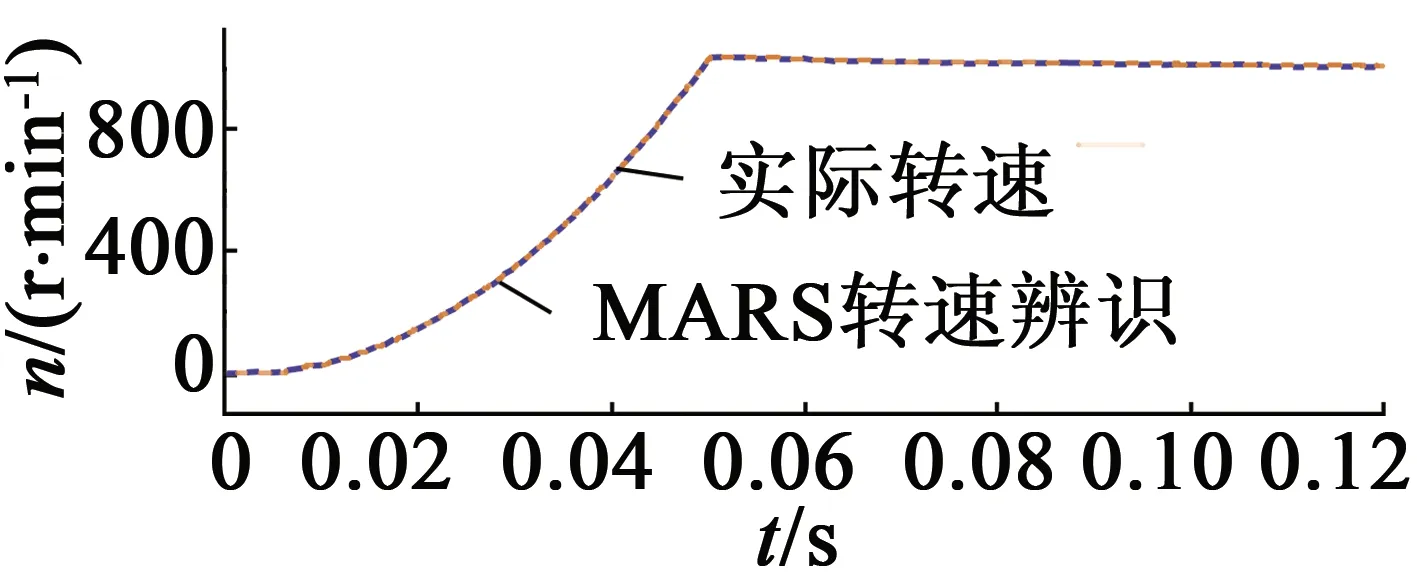
(b) 轉速響應

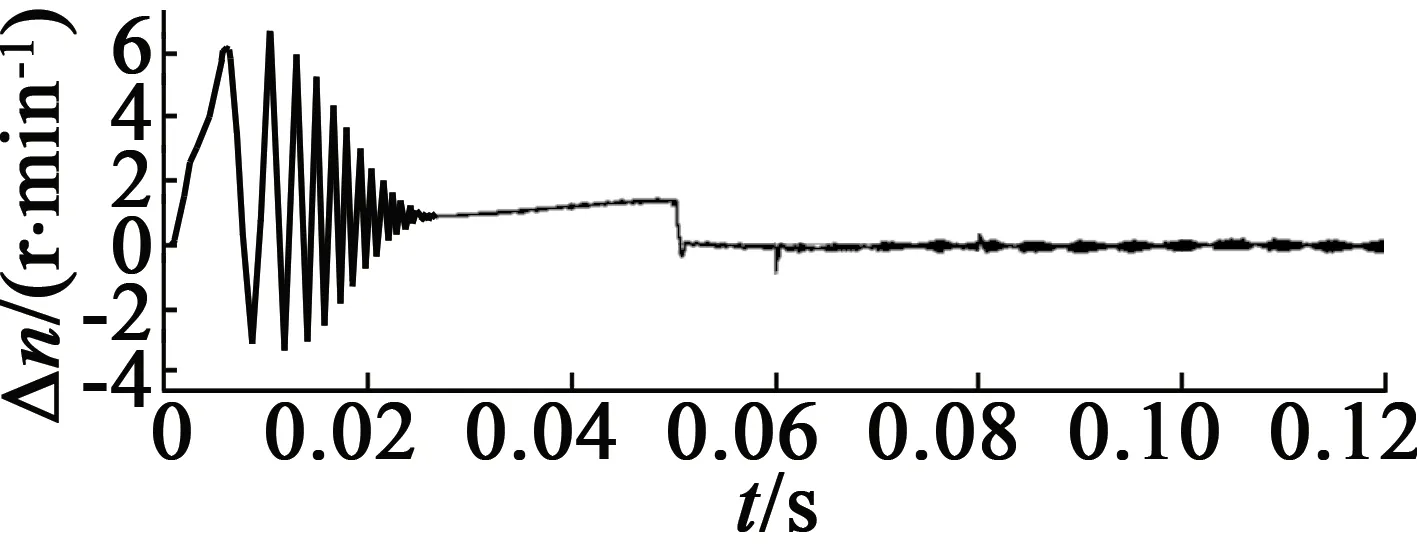
(c) 轉速誤差

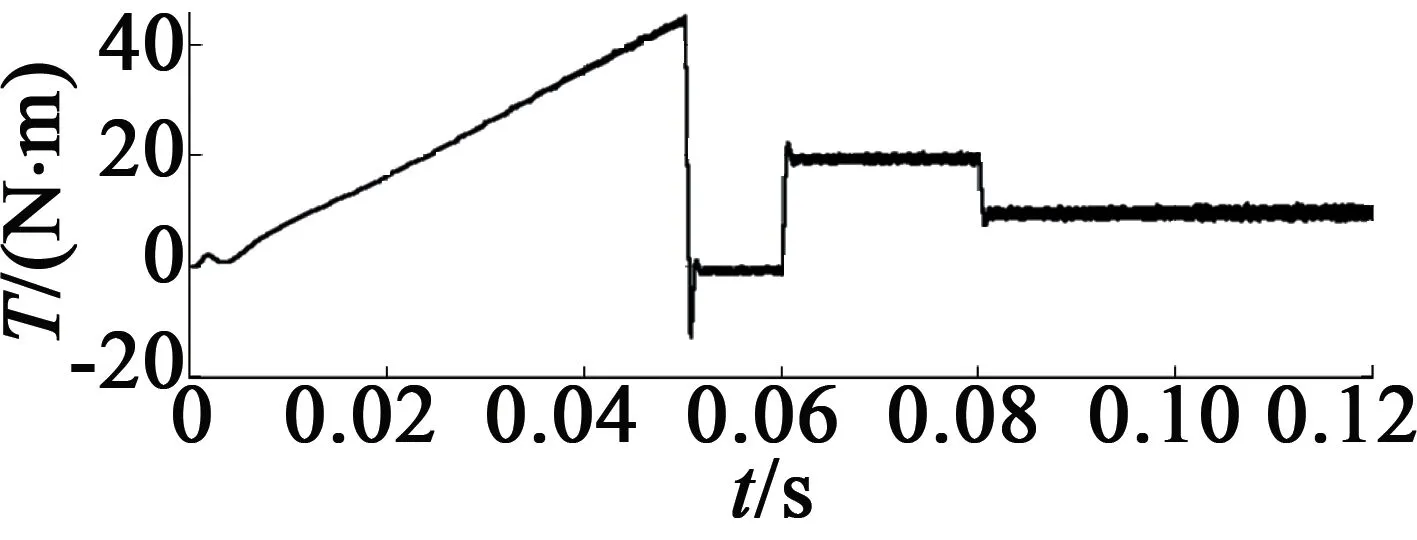
(d) 電磁轉矩

(e) 定子電流

4 結 語

本文以轉子磁鏈的電壓模型和電流模型作為MRAS速度觀測器的參考模型和可調模型，采用了一階慣性濾波環節消除電壓模型中的純積分問題，利用ADALINE在線權值修正的特點，設計了一種自適應神經元PID控制器，并將此控制器作為MRAS結構中的自適應機制。最后在轉速為1 000 r/min和2 200 r/min的情況下進行了仿真驗證，其結果表明，電機速度辨識精度較高，動態性能也得到了改善。