淺談高等數(shù)學(xué)中的思想方法及其教學(xué)建議

■張芙敏

（浙江東方職業(yè)技術(shù)學(xué)院）

數(shù)學(xué)是一門非常重要的學(xué)科，它與人類的生活和發(fā)展密不可分，社會主義現(xiàn)代化建設(shè)的各行各業(yè)都需要數(shù)學(xué)。認(rèn)識數(shù)學(xué)、研究數(shù)學(xué)、應(yīng)用數(shù)學(xué)到什么程度，主要看人們對數(shù)學(xué)思想方法掌握得怎么樣。[1]數(shù)學(xué)的顯性知識點如概念、定理、公式等可能會隨著時間的推移被淡忘，但基于顯性知識的數(shù)學(xué)思想方法它將化為內(nèi)生知識可隨時隨地發(fā)生作用。數(shù)學(xué)思想方法對人的能力的培養(yǎng)及素質(zhì)的提高都具有非常重要的作用。因此在高職高等數(shù)學(xué)教學(xué)中，我們應(yīng)加強滲透數(shù)學(xué)思想方法的教學(xué)。

1 高等數(shù)學(xué)中數(shù)學(xué)思想方法的主要內(nèi)容

所謂“思想”是：客觀存在反映在人的意識中經(jīng)過思維活動而產(chǎn)生的結(jié)果。而“方法”是：關(guān)于解決思想、說法、行動等問題的門路、程序等。

數(shù)學(xué)思想方法是人們對數(shù)學(xué)內(nèi)容本質(zhì)的認(rèn)識，是對數(shù)學(xué)知識的抽象與概括，屬于對數(shù)學(xué)規(guī)律的理性認(rèn)識的范疇[2]。

高職《高等數(shù)學(xué)》教學(xué)內(nèi)容主要包含函數(shù)與極限，導(dǎo)數(shù)與微分，導(dǎo)數(shù)的應(yīng)用，不定積分、定積分、定積分的應(yīng)用等。其中的數(shù)學(xué)思想方法可分為三類：一是思想觀點類。如：函數(shù)思想，極限思想，轉(zhuǎn)化思想，方程思想，數(shù)形結(jié)合思想等。二是思維方法類。如：猜想，歸納（從特殊到一般），分析與綜合，抽象與概括，觀察，類比，演繹與證明等等。三是技能技巧類。如：換元法，配方法，待定系數(shù)法，有理化，坐標(biāo)法等等。

2 高等數(shù)學(xué)教學(xué)過程中滲透數(shù)學(xué)思想方法教學(xué)的建議

在高等數(shù)學(xué)教學(xué)過程中數(shù)學(xué)思想方法教學(xué)是一項長期且需不斷挖掘的工作，需要教師們不斷總結(jié)、學(xué)習(xí)、分享。如何在高數(shù)教學(xué)過程中滲透數(shù)學(xué)思想方法，筆者認(rèn)為應(yīng)做到以下幾點。

2.1 教師在思想上應(yīng)重視數(shù)學(xué)思想方法教學(xué)

只有思想重視，才有行動支持。數(shù)學(xué)知識，如概念、定理、公式，都明顯地寫在教科書上，大綱有要求，肯定不會被忽視，而數(shù)學(xué)思想方法是隱于知識教學(xué)過程中，教學(xué)大綱考綱都不會被呈現(xiàn)，容易被忽視甚至忽略。所以教師只有在思想上重視數(shù)學(xué)思想方法教學(xué)，才會在教學(xué)過程中滲透數(shù)學(xué)思想方法教學(xué)。

教師在備課時可注意該知識點相關(guān)的數(shù)學(xué)思想方法，并從教材中不斷挖掘、提煉，并將該知識點涉及的數(shù)學(xué)思想方法與該知識點一同納入教學(xué)目標(biāo)中，這樣在做教學(xué)設(shè)計時必會設(shè)計好滲透數(shù)學(xué)思想方法的教學(xué)。

如在講導(dǎo)數(shù)的概念時，教師不僅要解決函數(shù)在某一點的導(dǎo)數(shù)“是什么”的問題，更要解決的是“是怎樣想到的”問題及在概念形成過程中所體現(xiàn)的極限思想。如導(dǎo)數(shù)定義引例中一例子。

已知自由落體運動的路程s與所經(jīng)過的時間t的關(guān)系是：

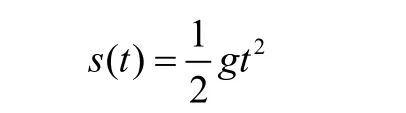
求：（1）3秒到3+Δt秒的平均速度；

（2）3秒時的瞬時速度。

在解該題時，教師不能只滿足解出題目結(jié)果，而應(yīng)將它的3秒時的瞬時速度如何實現(xiàn)等于3秒到3+Δt 秒的平均速度的這個思維過程傳給學(xué)生，也就是其中涉及的極限思想得讓學(xué)生感受到。

2.2 教師在教學(xué)中應(yīng)注意數(shù)學(xué)思想方法教學(xué)的反復(fù)性

數(shù)學(xué)思想方法尤其是思想觀點類的，它具有高度的抽象性，沒有固定的形式，有時只是一種思想意識，它需要教師反復(fù)滲透，不斷讓學(xué)生體會，才能逐漸被學(xué)生掌握。因此，教師在教學(xué)過程中，當(dāng)遇到類似數(shù)學(xué)思想方法時，應(yīng)不失時機地告訴學(xué)生，讓學(xué)生不斷體會，領(lǐng)悟，深化，才能達到有意地，自覺地應(yīng)用此思想方法。

例如前面提到的極限思想，當(dāng)講到定積分的概念時，又會涉及。教師應(yīng)抓住時機，讓學(xué)生再次體會、領(lǐng)悟。如：

【例2】 求曲邊梯形的面積。

解題主要過程：（1）分割——分曲邊梯形為n個小曲邊梯形

（2）近似代替——用小矩形的面積代替小曲邊梯形的面積

（3）求和——求n個小矩形面積之和

（4）取極限——由近似值過渡到精確值

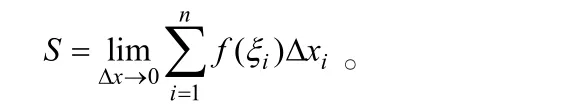
其第四步就涉及極限思想，在講到該點時，要注意讓學(xué)生體會、領(lǐng)悟極限思想。當(dāng)然，此時已是第二次講到該思想方法，教師在教案設(shè)計時要注意以引導(dǎo)為主，讓學(xué)生自己想到此思想方法，培養(yǎng)學(xué)生潛意識里會應(yīng)用此思想方法的能力。

2.3 教師在教學(xué)中應(yīng)注意數(shù)學(xué)思想方法教學(xué)的系統(tǒng)性

數(shù)學(xué)思想方法教學(xué)的系統(tǒng)性需從縱橫兩個方面去把握：縱向是這一數(shù)學(xué)思想方法在教學(xué)過程中可以借助哪些知識點來滲透；橫向是這一數(shù)學(xué)知識點可以進行哪些數(shù)學(xué)思想方法的滲透。教師在教學(xué)中應(yīng)注意從縱橫兩個方面對數(shù)學(xué)思想方法教學(xué)進行系統(tǒng)研究，從而能循序漸有的放矢的讓學(xué)生掌握相應(yīng)的數(shù)學(xué)思想方法。下面以縱向為例。比如構(gòu)造函數(shù)思想，它是一種重要的數(shù)學(xué)思想方法，在高等數(shù)學(xué)解題中經(jīng)常用到。高等數(shù)學(xué)教學(xué)中涉及該思想方法的有以下幾個知識點：

（1）零值定理。

如：【例3】證明方程x5-3x+1=0在區(qū)間（0，1）內(nèi)至少有一個根。

證明：令f(x)=x5-3x+1，則f(x)在[0,1]上連續(xù)。

又f (0) =1,f (1) =-1，

根據(jù)零值定理，有ξ∈(0,1)使f(ξ)= 0。

即 方程x5-3x+1 = 0在區(qū)間（0，1）內(nèi)至少有一個根ξ。

（2）最值問題——最小成本最大利潤問題。

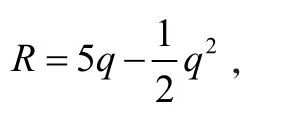
教師只有清晰課程中數(shù)學(xué)思想方法的系統(tǒng)內(nèi)容，才能在教學(xué)過程中更加自如地滲透數(shù)學(xué)思想方法的教學(xué)。

總之，數(shù)學(xué)思想方法是以數(shù)學(xué)知識點為基礎(chǔ)又高于數(shù)學(xué)知識點的一類隱性的數(shù)學(xué)知識。數(shù)學(xué)思想方法教學(xué)的重要性也已被越來越多的教學(xué)工作者們所重視。如何在教學(xué)中滲透數(shù)學(xué)思想方法仍是一個任重道遠的重要課題，需要廣大教學(xué)工作者們投入更多的時間和精力去共同探討和研究。