比例邊界計算機有限元算法理論及研究發展分析

余芝軒

(黃岡職業技術學院，湖北 黃岡 438002)

1 引言

隨著社會的發展與進步，新技術、新材料、新方法不斷出現，人類在社會生產活動中所面臨的工程日益復雜，越來越多的數值計算方法正在被人們所提出、接受以及研究。對于每一種數值計算方法，計算精度、計算效率以及適用范圍往往都是研究的重點。

計算機結合比例邊界有限元法是由John.P.Wolf 和Chongmin Song提出的一種結合了邊界元和有限元諸多優點的數值計算方法[1]。目前已有學者對此種方法進行了較為深入的研究，在工程領域進行了應用，并且和傳統的數值計算方法進行了對比。結果表明，對于某些工程實際問題，相比較于邊界元和有限元，此種方法可以顯著地減少計算時間，提高計算精度[2-3]。

2 比例邊界有限元法的理論基礎

對于二維彈性靜力學來說，應力{σ(x,y)}和體積力{p(x,y)}在域內任一點應滿足如下關系：

[L]T{σ(x,y)}={p(x,y)}

(1)

這里[L]是線性微分算子。

應變{ε(x,y)}和位移{u(x,y)}的表達式如下：

{ε(x,y)}=[L]{u(x,y)}

(2)

而應力與應變的關系表達式如下：

{σ(x,y)}=[D]{ε(x,y)}

(3)

其中[D]是彈性矩陣。

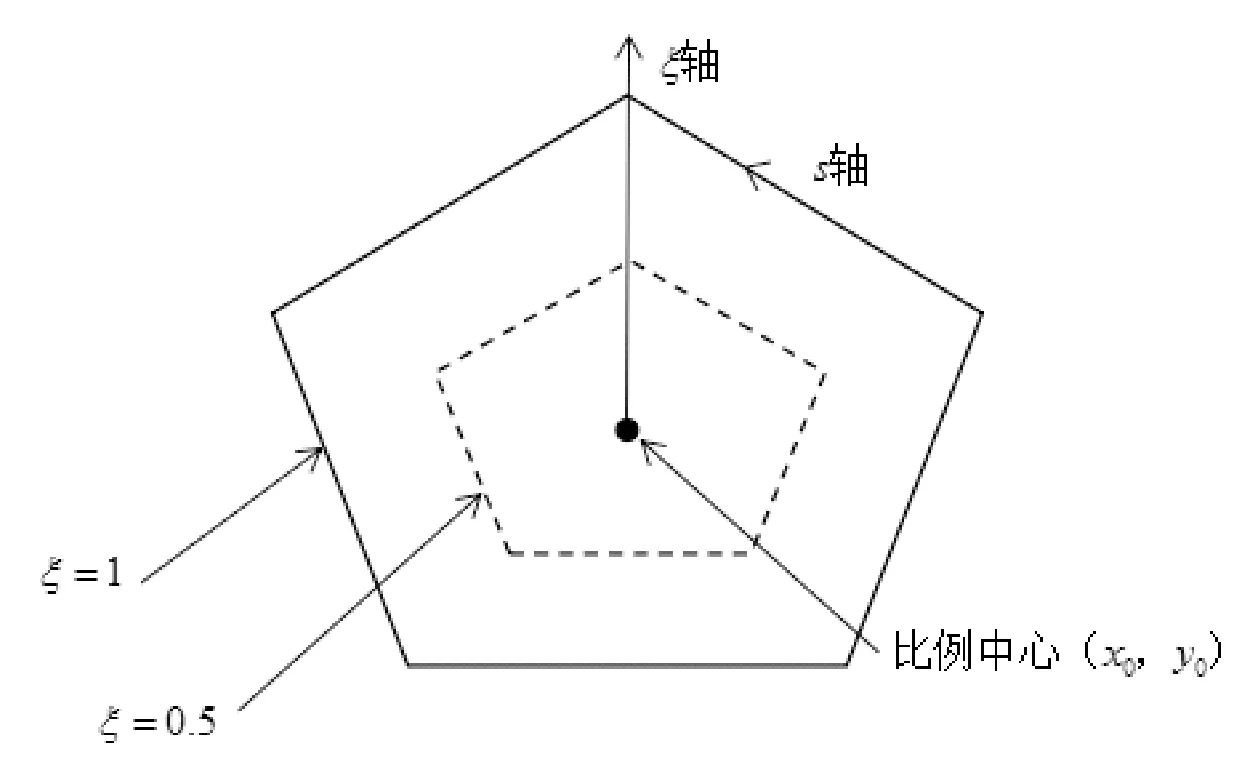
圖1 比例邊界有限元坐標系統

在推導比例邊界有限元方程時，需在比例中心(x0,y0)建立相應的坐標系。比例中心可以在對所有邊界可見的前提下放在域內任意位置[4]。比例邊界元的坐標系統包括徑向坐標ξ和環向坐標s。徑向坐標規定，在比例中心處ξ=0，在邊界上ξ=1，域內其他地方取0<ξ<1；環向坐標指沿著邊界逆時針方向的距離。

笛卡爾坐標下的點(x,y)可以由ξ和s表示為：

x=x0+ξxs(s)=x0+ξ[N(s)]{x}y=y0+ξys(s)=y0+ξ[N(s)]{y}

(4)

運用雅克比矩陣變化，可得：

(5)

其中，雅克比矩陣

(6)

在ξ=1的邊界上，式(6)的[J(ξ,s)]將變成[J(s)]，且[J(s)]只與邊界上的節點坐標有關，矩陣形式為：

(7)

即

[J(s)]=x(s)y(s)s-y(s)x(s)s

(8)

結合式(5)和(6)，可得：

(9)

其中，

|J(ξ,s)|=x(s)ξy(s)s-y(s)ξx(s)s=ξ[x(s)y(s)s-y(s)x(s)s]=ξ|J(s)|

(10)

將式(10)帶入式(9)，可得：

(11)

對于二維的線彈性問題，

(12)

將式(11)代入(12)，可得：

(13)

其中，令

(14)

(15)

將式(14)和(15)代入(13)，可得：

(16)

同時，令

[B1(s)]=[b1(s)][N(s)],[B2(s)]=[b2(s)][N(s)]s

(17)

采用如下的虛功原理表達式進行相應的變化和推導：

(18)

對式(17)進行相應的積分和運算，可得到比例邊界有限元下關于{uh(ξ)}ξξ、{uh(ξ)}ξ、{uh(ξ)}以及系數[E0]、[E1]、[E2]的Euler-Cauchy位移平衡微分方程，并可得到相應解為

{uh(ξ)}=c1ξ-λ1{φ1}+c2ξ-λ2{φ2}+…+ciξ-λi{φi}

(19)

其中，ci代表的是每一種獨立的位移模式對于方程解的加權系數，-λi則表示了對于徑向坐標的比例因子。

通過對方程自由度數的翻倍，可構建一個關于不同模態下的位移以及節點力的特征方程并進行求解。

對于式(19)中的ci，一般通過在邊界上(ξ=1)的方程{c}=[Φ1]-1{uh}來求得。并最終可以得到位移和應力的表達式分別為：

(20)

(21)

3 比例邊界有限元法研究進展

比例邊界有限元法(SBFEM)是一種基于計算機有限元方法，并且結合了有限元和邊界元諸多優點的較為新型的數值方法。相比較于邊界元，比例邊界有限元同樣只需要在邊界上進行離散，但它針對邊界元無法生成對稱剛度矩陣的問題做出了相應改進。目前，已有研究和工程實踐表明，比例邊界有限元對于解決應力奇異性問題以及無限域問題，相對于傳統的有限元方法來說具有很大的優勢。對于應力奇異性問題，比例邊界有限元法不需要進行額外的處理。在無限域問題上，由于SBFEM只需在邊界上進行離散，從而可以在處理相關問題時通過更少的自由度數來提高計算效率，減少計算時間[5]。Hauke Gravenkamp、Carolin Birk和Chongmin Song在2015年對彈性導波在帶有缺陷的無限域板中的傳播進行了模擬，并在建模效率和計算精度這兩方面將模擬結果與傳統有限元在同等條件下的模擬結果進行了比較。結果表明，在精度相同的情況下，比例邊界有限元的建模效率可以提高兩到三倍。

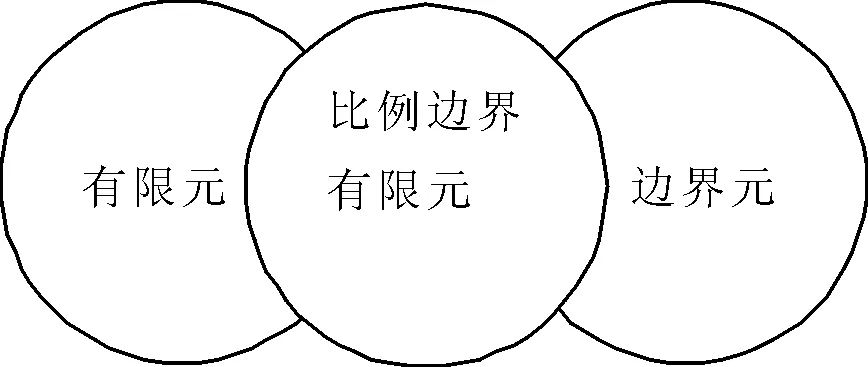
圖2 比例邊界有限元關系圖

除此之外，比例邊界有限元在裂縫問題的處理上也有獨到的優勢，其可以通過將比例中心設置在裂尖上來解決應力奇異性的問題。而且裂縫位置的變化以及裂縫深度的改變也僅需要進行少量的網格重劃分即可完成，相比較于有限元法來說大大減少了工作量。Hauke Gravenkamp、Jens Prager、Albert A.Saputra和Chongmin Song對Lamb波在帶有裂縫板中的傳播進行了模擬，并在自由度數(DOF)、誤差(Deviation)和運行時間(CPU)這三個方面對SBFEM與傳統有限元的模擬結果進行了綜合比較，結果表明在誤差率一致的情況下，比例邊界有限元的自由度數僅有傳統有限元法的5.88%，運行時間僅有傳統有限元法的1.50%。從以上工程實例可以得知，在裂縫問題的模擬以及計算過程中，比例邊界有限元的計算效率相比較于傳統有限元法有了較為明顯的提升。

正是由于比例邊界有限元法(SBFEM)在各種工程實際問題中得到了不斷的應用并且相比較于傳統有限元方法在某些方面有了較為明顯的進步，所以近年來，比例邊界有限元法得到了越來越廣泛的認可、研究、應用以及發展。

比例邊界有限元最初是用來計算無邊界介質的動力剛度矩陣，然后Chongmin Song和J.P.Wolf又用此方法對多項異性材料進行裂縫分析[6]。隨后，在此前工作的基礎之上，J.P.Wolf和A.J.Deeks對比例邊界有限元的原理以及坐標變化做了系統的闡述，即推導了從笛卡爾坐標系統到徑向、環向坐標系統的轉變，且進一步擴寬了其適用范圍。隨后Chongmin Song對靜力學問題又提出了一種新的矩陣函數計算方法，并表明此種計算方法具有更高的計算精度[5]。大連理工大學的林皋院士和他的博士生杜建國將比例邊界有限元應用于計算壩面動水壓力，通過對二維以及三維的動水壓力進行計算，并且和有限元的計算結果進行對比發現，比例邊界有限元可以在提高計算效率、減少工作量的同時減小計算誤差[7]。Hauke Gravenkamp和Albert A.Saputra等人首次將比例邊界有限元應用于模擬蘭姆波在帶裂縫板中的傳播，結果表明對于裂縫問題，比例邊界有限元在計算誤差減小、計算時間大幅度縮減的同時，計算模型仍然具有比有限元少的自由度數[8]。之后，Hauke Gravenkamp和Carolin Birk等人繼續模擬了彈性導波在任意邊界的帶缺陷條形板中的傳播并推導出了動力剛度矩陣[9]。Ean Tat Ooi和Chongmin Song等人又提出一種基于比例邊界的多邊形網格劃分方法，和以往的研究對象均是線彈性材料不同，此方法對彈塑性材料進行了模擬、分析，從而大大擴寬了比例邊界有限元方法在未來的應用領域[10]。此后，陳燈紅和戴上秋等用比例邊界有限元做了土體-結構交互作用的動態斷裂分析，并且得出了相對于傳統方法更加準確和有效的計算結果[11]。

4 總結

本文針對目前一種較新型的數值計算方法——比例邊界有限元法(SBFEM)，對其理論基礎、坐標變化等方面做了推導，對比例中心的選取及適用范圍做了詳細的闡述。目前已有研究以及相應的工程算例在計算精度、計算效率等方面將SBFEM和傳統的有限元方法進行了比較。計算結果表明由于SBFEM僅在邊界上進行離散，具有降低維度、減少自由度的特點，故可以在提高計算效率的同時減小計算誤差。

隨著研究的深入，比例邊界有限元法在解決應力奇異性、無限域以及裂縫問題上已不斷地顯示出良好的適應性、便利性和快捷性。相信隨著研究的不斷深入與在工程領域的不斷應用，結合計算機比例邊界有限元法會在今后得到越來越廣泛的應用。