“基于問題和任務”教學模式的探究
高路 王乾生 林軍
[摘要]“以任務探索生成問題,以問題思考形成知識,以文化滲透豐富內涵”的課堂教學模式,體現以學生發展為本的現代教育理念,可極大提高課堂教學效率。
[關鍵詞]任務,問題,文化,曲線與方程
[中圖分類號]G633.6[文獻標識碼]A [文章編號]1674-6058(2020)11-0005-03
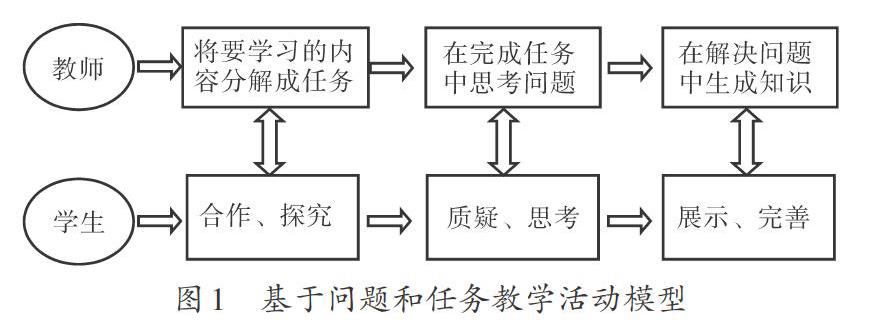
廣西普通高中學科基地建設柳州高級中學數學課程基地自建成以來,以探索適合學生發展的、有數學味的高效課堂為建設目標,形成了以“以任務探索生成問題,以問題思考形成知識,文化滲透豐富內涵”的課堂教學模式(如圖1)。
2019年11月20日,我校高路老師參加柳州市青年教師賽教課,課題是《曲線與方程》,教學設計采用“基于問題和任務”的教學模式,得到評委及聽課教師的一致好評,獲得了柳州市青賽課一等獎,以下是本節課的課堂實錄,希望通過實錄這種形式,能更加直觀地讓一線教師了解此教學模式的基本步驟和實施路徑。
[課堂實錄]
一、創設情境,豐富內涵
師:人類對曲線與方程的認識經歷了一個漫長的過程,下面請同學們觀看視頻,看看費馬和笛卡爾研究曲線的方法,與阿波羅尼奧斯有什么不同。
(學生觀看視頻)解析幾何的發展史,
1.古希臘數學家阿波羅尼奧斯采用平面切割圓錐的方法,得到了圓、橢圓、雙曲線、拋物線,并從純幾何的觀點研究了圓錐曲線的性質,后人幾乎無法突破。
2.費馬,17世紀法國數學家,通過引進坐標,從方程出發研究幾何曲線的軌跡。
3.幾乎同一時期,法國另一位數學家笛卡爾,引入坐標法,從軌跡開始建立方程。
雖然費馬的研究是從數到形,笛卡爾是從形到數,但他們都建立了坐標系,引入坐標,將方程與曲線聯系起來,創立了解析幾何。
設計意圖:將數學史融入課堂,鏈接了章導言,既激發了學生的學習熱情,又讓學生了解數學家研究曲線的方法,使課堂的文化味更濃。
二、自主探究,生成概念
任務活動一:請在平面直角坐標系中,畫出方程2x2-y=0(x≠0)對應的曲線,并思考:
問題1:你用了什么方法畫曲線?
問題2:曲線上的點坐標從何而來?
生:問題l是采用描點法,
生:問題2是從方程的解中選取,
師:剛才有些同學沒有在曲線中挖掉原點,為什么要挖掉原點?
生:因為題設要求x≠0.
師:若不挖掉原點,從圖形直觀來看,以方程的解為坐標的點與曲線上的點相比,誰多誰少?
生:點多解少。
師:我們只是選取了幾個點描出曲線的大致圖形,是否可以認為以這個方程的所有解為坐標的點都在對應曲線上,這樣的猜想合理嗎?
生:我們作圖都用描點法,這當然是對的,
為了驗證猜想,學生給出方程的任一組解,教師用幾何畫板演示以這些解為坐標的點都在曲線上,
師(追問):若以方程的解為坐標的點都在曲線上,則誰的點的個數有可能多?
生:曲線上的點有可能多。
師:此時,若把方程的解集和曲線上的點集分別用集合A、B表示,A、B有什么關系?
生:A是B的子集。
設計意圖:讓學生經歷描點法作圖,能更直觀地體會以方程的解為坐標的點都在曲線上,實現從數到形的轉化,為學生理解方程的曲線這一概念提供實例。
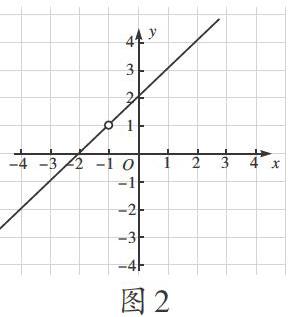
任務活動二:求如圖2所示的曲線對應的方程,并思考:
問題3:你是用什么方法求方程的?
生:直線過(-2,0)和(0.2),我是將兩點代人斜截式求出直線方程x-y+2=0(x≠1)的,
師:你能否保證直線上所有點的坐標都滿足你選用的這兩點所求的方程?
生(遲疑后):應該是吧。
教師操作幾何畫板,在曲線上任取一點,度量其坐標,讓學生充分感知,不管點如何移動,點坐標始終滿足所求方程。
師:如果所求方程沒有限制x≠-1.顯然,方程的解比曲線上的點多,若曲線上的點坐標都是方程的解,則誰的個數有可能多?
生:解有可能多。
師(追問):此時,若把方程的解集和曲線上的點集分別用集合A、B表示,A、B有什么關系?
生:B是A的子集。
設計意圖:讓學生經歷求直線方程的過程,學生能更直觀地體會曲線上的點坐標都滿足方程,實現從形到數的轉化,為學生理解曲線的方程這一概念提供實例。
任務活動三:請分別畫出曲線C:到坐標原點距離為1的圓在y軸右側部分,和方程f(x,y)=O:x2+y2=1(y>0)表示的曲線,并思考:
問題4:曲線C上的點集A與方程f(x,y)=0的解集B有包含關系嗎?
生:沒有。
師:這樣兩者間不能建立某種對應關系。
設計意圖:對概念的理解不光要深究其內涵,還要明白其外延,提供方程的解集與曲線的點集間沒有相互包含關系的實例供學生辨析是很有必要的。
師:通過這三個例子,請大家想一想,要使方程與曲線能夠相互表示,以方程的解為坐標的點與曲線上的點間應該能夠建立怎樣的對應關系?(學生小組討論)
生:方程的解與曲線上的點一樣多。
師:對,一點不多,一點不少,那么我們能否將“方程的解與曲線上的點一樣多”這一條件更加“數學化”
一點呢?(學生回答,互相補充)
(教師板書方程與曲線的定義)
設計意圖:通過提供豐富的實例去揭示概念的本質屬性,從而促成概念的生成。
三、深化概念,鞏固內化
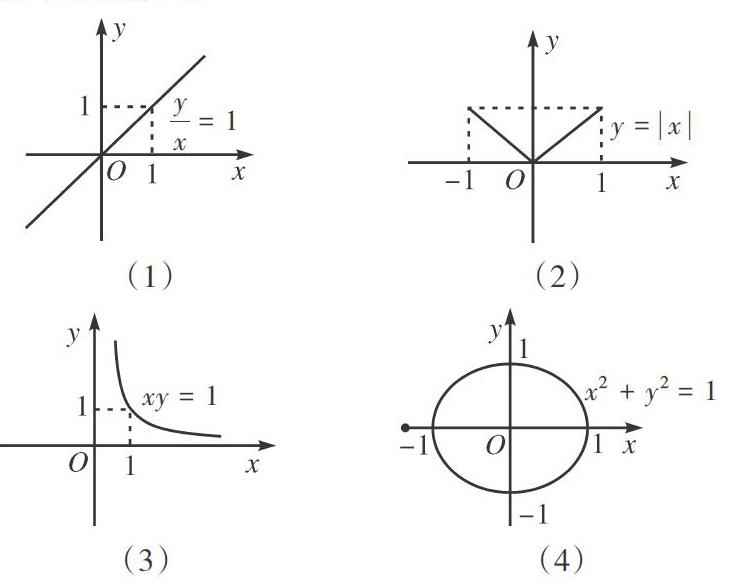
任務活動四:判斷圖3的方程能否叫作曲線的方程,曲線能否叫作方程的曲線,并思考:
問題5:當方程與曲線不一致時,你能否修改曲線或方程中的一個,使得方程變成曲線的方程,曲線變成方程的曲線?
設計意圖:通過修改方程或曲線中的一個,使二者能建立一一對應關系,這是對方程與曲線概念的再認識與升華。
師:任務活動四要判斷曲線與方程不對應,只需舉反例,但要說明題(4)中方程與曲線是一一對應的,就必須嚴格加以證明,那么如何證明呢?
生:從曲線和方程定義的兩個方面進行,
師:請完成下列作業。
證明:以坐標原點為圓心,半徑等于1的圓的方程是x2+y2=1.
(給學生充分的時間思考后,請一個學生展示其證明過程)
生(恍然大悟):點(X0,Y0)到原點的距離等于1.所以方程的解為坐標的點在圓上,
師:在上述證明過程中,無論是取圓上一個點,還是取方程的一組解都是任意的,并且都滿足曲線和方程定義的兩個方面,所以我們就嚴格證明了該命題,
設計意圖:本教學環節的設計,一是讓學生明白數學是嚴謹的,當你肯定一個問題時,就要給出嚴謹的證明;二是讓學生學會證明方程與曲線的關系,進一步理解方程與曲線的概念,學會數與形間的轉化。
四、課堂小結,總結提升
師:本節課我們收獲了哪些知識?用到了什么思想方法?
(學生談體會談感受,相互補充,如圖4)
師:方程與曲線是整個解析幾何的基石,把曲線用方程表達,就為我們用代數方法研究幾何問題提供了有力的保障,為接下來進一步研究圓錐曲線奠定了基礎。
設計意圖:課堂小結是對一節課的一個高度概括,有助于學生理順知識,形成方法,深化概念,提升能力。
五、作業布置(略)
[教學反思]
1.社會的發展帶來育人觀念的轉變,數學文化融入課堂成為必然,曲線與方程有著豐富的數學文化背景,以解析幾何發展史為素材引入新課,讓學生了解數學家研究手段的變遷,感知數學思想,
2.任務設計強調目的性與針對性,曲線與方程的概念是非常抽象的,學生難以理解,但這個概念兼具形與數的特征,所以設計任務活動一、任務活動二、任務活動三的目的就是實現從數到形、形到數、數形互化的轉變,實例典型豐富,引起學生的認知沖突,利于學生數學抽象素養的養成,任務活動四通過辨析正、反兩方面的實例,不僅需要判斷,還需要嚴謹論證,這對培養學生的邏輯推理能力意義重大。
3.問題設計有啟發性和思考價值,由任務引出的問題從學生思維的最近發展區出發,激發了探索欲望,啟發學生思考,充分暴露其思維過程,落實重點,化解難點,提高了課堂教學效率。

