淺析距離交會歸化法定位精度

郭一江 李靖銘

摘? 要：距離交會法廣泛應用于工程放樣中，按照施工放樣條件選擇對應的歸化方式可有效提高點位精度，進行距離交會時，以兩已知點為圓心按照各自半徑做圓相交，初步確定放樣點位，由于測量工作不可避免誤差，因此所得點位與絕對位置存在橫向和縱向的偏移量，對此應按交會角范圍選擇歸化方式，處理時以同三角形中角度和邊長關系引入交會角，選擇按偏移量平行或垂直于偏移量所得兩個交點分別進行歸化討論，得出準確放樣點位。若在距離交會放樣時判斷交會角范圍并選擇對應歸化方式可有效提高放樣點位精度。

關鍵詞：距離交會歸化? 交會角? 偏移量? 放樣精度

中圖分類號：P271 ? ?文獻標識碼：A 文章編號：1672-3791（2020）03（c）-0205-02

Abstract： Distance intersection method is widely applied in the project lofting， according to the conditions of construction lofting choose corresponding naturalized way can effectively improve the positional accuracy， distance intersection， with two known points as the center of the circle radius of respective do circular intersection， preliminary determine lofting point， due to the measurement error is inevitable， so the income level of horizontal and vertical offset with absolute position， this should choose naturalized way according to the intersection Angle range， processing with triangle Angle and side length relationship into the intersection Angle， choose according to the offset parallel or perpendicular to offset the two intersection naturalization discussed respectively， precise lofting points are obtained. If the range of intersection Angle is determined and the corresponding domestication method is chosen during the distance from the intersection lofting， the lofting point position accuracy can be effectively improved.

Key Words： Distance intersection naturalization; Intersection Angle; The offset; Lofting precision

歸化法是精確放樣點位的一種方法，在距離交會中無法放樣出精確點位，在此基礎上后續進行誤差計算求解偏差值。但在實際工程中采用距離交會歸化時常直接對求解出的兩偏移量進行平行處理，兩直線平行后交于一點并將此點作為歸化后精確點，其實都這樣處理并不是最嚴謹的處理方式，在此基礎上引入交會產生的角度，進一步考慮距離交會時產生的夾角在不同取值范圍時采用的歸化方式對點位精度帶來的影響。

1? 距離交會歸化法

1.1 距離交會歸化原理

假設放樣點為P1，為了將P1點放樣出來，首先根據P1點設計坐標及控制點A、B的坐標計算放樣元素S1、S2。以A、B為圓心，以S1、S2的距離為半徑作圓弧，兩弧線的交點即放樣點P1。進行距離交會放樣過程中放樣值與理論計算值S1、S2因測量工作中不可避免的誤差，所以存在偏移量，設S1偏移量為s1，S2偏移量為s2。A、B為控制點，按照設計值P1計算出理論值S1、S2以及交會角γ。

1.2 歸化方式

以偏移量作垂線、平行線歸化。

如圖1所示，過偏移量s1、s2作垂線相交于P2點，以偏移量s1、s2作AP1、AP2平行線相交于P3點。

2? 歸化討論

2.1 偏移量變化情況

假設理想放樣邊長為AP1、BP1，實際放樣邊長為S1、S2，由于測量中存在儀器誤差、人為誤差、偶然誤差，因此，AP1≠S1、BP1≠S2，則偏移量情況如下。

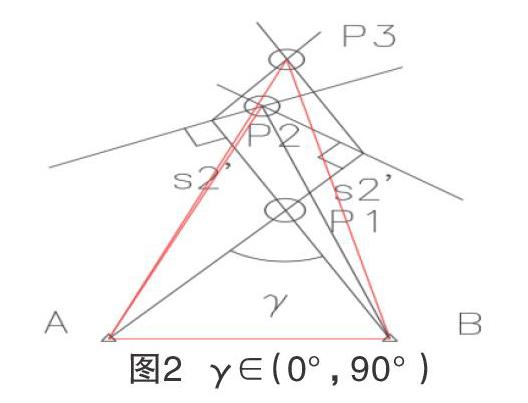
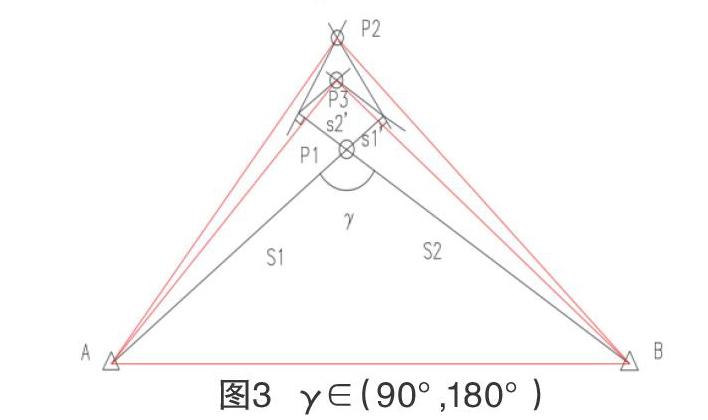
S1BP1;S1>AP1，S2>BP1;S1>AP1，S2

2.2 距離交會角情況

在進行距離交會前將已知數據計算得出交會角，設交會角為γ（度），并判斷其區間，對不同區間偏移量的歸化方式分別討論，交會角的區間分3種情況：γ∈（0°，90°）;γ=90°（臨界條件）;γ∈（90°，180°）。

2.2.1 當γ∈（0°，90°）

如圖2所示，當γ大于0°小于90°時，垂線歸化和平行歸化構成以AB邊為公共邊的兩個三角形，在此情況下，平行歸化產生的交點構成的三角形ABP3包含按垂線歸化產生的交點構成的三角形ABP2，若將AP3看作集合U，那么AP2為AP3的一個子集。

此時將三角形ABP2在ABP3中分析，理論值AP1、偏移量均是定值，設AP2與偏移量的差值為ε1，設AP3與偏移量的差值為ε2，當差值更逼近于AP1，即εi-AP1趨近于0時，精度較高，在同三角形中分析中，當γ∈（0°，90°）時，AP2為AP3的一個子集，即AP2

從三角函數角度分析，由于實際正確放樣后產生偏移量非常小，則產生的偏角極小，設垂直歸化產生的偏角為δ1、平行歸化產生的偏角為δ2，且δ1<δ2，此時將三角形AP1P2、AP1P3近似為直角三角形，=cosδ1，=cosδ2，當δi∈（0°，90°）時，余弦函數的值隨角度的增大而減小，推出AP2

2.2.2 當γ=90°

當γ=90°時，進行垂線歸化和平行歸化時交點P2于P3相重合，此種情況放樣精度從歸化方式可認為相等。

2.2.3 當γ∈（90°，180°）

如圖3所示，當180°>γ>90°時，垂線歸化和平行歸化構成以AB邊為公共邊的兩個三角形，在此情況下，垂線歸化產生的交點構成的三角形ABP2包含按平行歸化產生的交點構成的三角形ABP3，若將AP2看作集合U，那么AP3為AP2的一個子集。

此時將三角形ABP3在ABP2中分析，理論值AP1、偏移量均是定值，設AP2與偏移量的差值為ε1，設AP3與偏移量的差值為ε2，當差值更逼近于AP1，即εi-AP1趨近于0時，精度較高，在同三角形中分析中，當γ∈（90°，180°）時，AP3為AP2的一個子集，即AP3ε2，因此AP3更逼近理論值。

從三角函數角度分析，同理可證得AP2>AP3，即AP3加上偏移量更逼近于理論值，證得，當γ∈（90°，180°）時，平行歸化時高于作垂線歸化時的精度。

3? 結語

在使用距離交會法放樣時應根據已有參數計算并判斷交會角，對交會角不同的取值選擇相應的歸化方式，當交會角γ∈（0°，90°）時，應選擇垂直于偏移量的方式進行歸化，當γ=90°時，從歸化方式的角度，作垂線歸化與平行歸化時精度相同，當γ∈（90°，180°）時，選擇平行歸化時的精度優于作垂線進行歸化。

參考文獻

[1] 寧津生，陳俊勇，李德仁，等.測繪學概論[M].2版.武漢：武漢大學出版社，2015：136-137.

[2] 周保興，朱愛民.工程測量學[M].北京：人民交通出版社股份有限公司，2018：67-68.

[3] 李建豪.距離交會的誤差估算及應用[J].城市勘測，2010（3）：119-121.