關于函數壓軸題的解題策略探討與建議

周華

[摘 ?要] 函數壓軸題的解題過程是知識調用、問題轉化的過程，該過程中需要使用相應的解題技巧，其中數形結合是直觀呈現問題、構建模型、嚴密推理的常用策略. 文章通過分析函數壓軸題，思考數形解題策略，結合實例探討函數壓軸題的突破過程，提出相應的教學建議.

[關鍵詞] 函數;策略;思想;數形結合

函數是初中數學的重點內容，也是知識綜合性最強的內容之一. 縱觀近幾年的中考題，函數作為壓軸題出現的頻次很高，常聯合平面幾何、代數方程、不等式等內容來命制考題. 命題特征鮮明，常采用連續設問方式，難度逐問遞增，各問之間具有一定的關聯性和鋪墊作用，能夠引導學生思考，全面考查學生的知識水平和邏輯推理能力.

實際上函數是數形結合最為緊密的內容，函數解析式與圖像之間存在著對應關系，從思想層面來看，是對數形結合思想的體現. 函數問題考查的知識內容十分豐富，在實際研究時需要全面考量函數圖像，分析變量關系，總結結論. 基于數形結合思想建議采用如下解題策略：

1. 畫圖解信息，由圖析關系（由形析數）

對于函數壓軸題可利用圖像來解析題干條件，提取隱含信息. 首先繪制圖像，充分解讀題干條件，利用圖像的直觀性來挖掘其中的幾何特性.

2. 列式得未知，代數分析解（用數解形）

把握隱含信息，利用圖像中的點來求解所涉函數關系式，通過解方程、不等式或函數分析的方式來獲取關鍵量，逐步剖解問題.

考題探究

函數壓軸題的綜合性很強，其解法也不唯一，從不同的角度分析可以獲得不同的信息條件，但均可以按照上述所推薦的數形策略來構建思路，下面以一道函數壓軸題為例加以探討.

問題：（函數與幾何的綜合）已知拋物線的解析式為y=ax- 2-2，其頂點為A，點B- ，2和C ，2是拋物線上的兩個點，試回答下列問題.

（1）求該拋物線的解析式;

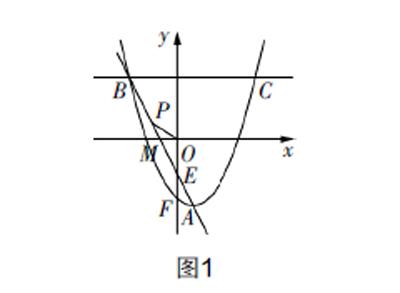
（2）如圖1所示，過點A和B的直線與x軸和y軸的交點分別為點M和E，拋物線與y軸的交點為F，點P位于直線AB上，若有∠OPM=∠MAF，試求△POE的面積;

（3）如圖2所示，點Q位于折線A-B-C上，過點Q作y軸平行線，再過點E作x軸的平行線，設兩線交點為N，將△QNE沿著直線QE翻折，可得△QEN1，若點N1剛好落在x軸上，試求點Q的坐標.

思路突破：

第（1）問求拋物線的解析式，只需要將拋物線上已知坐標的一點代入解析式即可，將- ，2代入y=ax- 2-2中，可解得a=1，則該拋物線的解析式為y=x- 2-2.

第（2）問求所構三角形的面積，核心條件是等角關系“∠OPM=∠MAF”. 基于數形結合策略進行問題分析，根據條件信息理解圖像，顯然△POE由直線AB、OP和y軸合圍所成. 點A坐標已知，點B、E、F、M的坐標均可以聯立方程獲得. 連接AF后，由“∠OPM=∠MAF”可知OP∥AF，后續需要分兩步進行：第一步構建面積模型，第二步利用條件列方程求相關未知量. 有以下兩種方法.

若將△POE視為以OE為底、點P為頂點的三角形，則其面積可以表示為S△POE= ·OE·h，其中h表示點P到y軸的距離，數值上與點P橫坐標的絕對值相等. 將直線AB的解析式設為y=kx+b，分別代入點A和B的坐標，則可求得解析式為y=-2x-1，從而可得點E（0，-1），F0，- ，M- ，0. 由∠OPM=∠MAF可知OP∥AF，從而可證△OPE∽△FAE，由相似性質可得 = . 其中利用兩點之間的距離公式可得OE=1，EF= ，AF= ，代入可解得OP= . 點P位于直線AB上，可將其坐標設為（t，-2t-1），從而可解得t1= - ，t2=- ，分析可知點P的兩個位置均滿足等角條件，將其分別代入面積模型可求得△POE的面積，當t1=- 時，可得S△POE= ;當t2=- 時，S△POE= ，所以△POE的面積為 或 .

第（3）問涉及幾何折疊，同時點Q在折線A-B-C上運動，需要利用折疊特性進行分類討論. 結合圖像分析可知需要分為三種情形：①點Q在AB上運動，②點Q在BC上運動，且位于y軸的左側;③點Q在BC上運動，且位于y軸的右側. 具體分析時需要提取其中的基本圖形，結合圖形性質來構建方程求坐標.

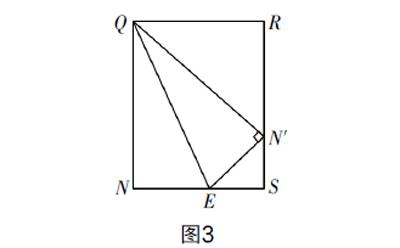
①當點Q在AB上運動時，如圖3所示，設點Q（a，-2a-1），則NE=-a，QN= -2a，根據翻折特性可得QN′=QN=-2a，N′E=NE=-a. 分析可知△QRN′～△N′SE，根據相似性質可得 = = ，代入可解得QR=2，結合NE+ES=NS=QR，可得-a+ =2，則a=- ，所以點Q的坐標為- ， .

②當點Q在BC上運動，且位于y軸的左側時，如圖3所示. 設NE=-a，則N′E=-a，易得RN′=2，SN′=1，QN′=QN=3，則QR= ，SE= +a. 在Rt△SEN′中使用勾股定理可得SE2+SN′2=EN′2，解得a=- ，所以點Q的坐標為- ，2.

③當點Q在BC上運動，且位于y軸的右側時，如圖4所示，按照情形2的思路進行方程構建，設NE=a，則N′E=a，易得RN′=2，SN′=1，QN′=QN=3，則QR= ，SE= -a. 在Rt△SEN′中使用勾股定理可得SE2+SN′2=EN′2，解得a= ，所以點Q的坐標為 ，2.

綜上可知，滿足條件點Q的坐標有三個，分別為- ， 、- ，2和 ，2.

上述是拋物線與平面幾何相綜合的壓軸題，其中涉及幾何角相等、求解三角形模型、圖形翻折等幾何內容，這也是函數綜合題常見的命題方向. 上述采用了數形結合構建思路的策略，過程中體現了該策略解題的三個關鍵點：一是利用圖像來理解題意，這是解題的前提;二是利用圖像來轉化條件，主要體現在后兩問上，以第（2）問為例，結合圖像將等角關系轉化為三角形相似關系，以及直線斜率相等關系;三是利用圖像模型來構建方程，無論是求直線解析式，還是求點坐標參數，均體現得淋漓盡致.

解后反思

函數與幾何壓軸題的突破需要完成圖像分析與代數轉化兩個過程，上述呈現了數形結合解題的具體步驟，下面提出兩點教學建議.

1. 重視觀察，探析特性

函數與幾何壓軸題的特點是信息含量大，圖像較為復雜，基于數形結合開展解題教學時需要使學生明晰信息理解的重要性，包括文字、符號和圖像信息，在該階段要完成題干條件與問題圖像的對照轉化. 因此需要引導學生重視觀察圖像，掌握讀圖技巧，例如提取曲線與坐標的交點、曲線之間的交點，關注其中的特殊圖形，提取圖形特性，以此為切入點來挖掘隱含條件，構建相應的思路. 考慮到圖像較為復雜，具體教學時可以采用簡圖分析的方式，引導學生對復合圖形進行拆解，構建模型，如上述第（3）問分類討論時分別提取了動點圖模型.

2. 直觀猜想，嚴謹論證

函數壓軸題所涉線條較多，結合了幾何運動內容的問題更為復雜，部分幾何元素的內容不完全確定，此時就需要引導學生發揮想象來做出猜想. 猜想時需要整合題干中的基本條件，綜合考慮、合理猜想，例如上述結合條件可以想到點P的位置有兩個，后續只需要加以論證即可. 在論證過程中需要充分運用函數與幾何性質，構建相應的方程、不等式，通過求解獲得準確的點坐標、取值范圍等內容，從而剔除其中的錯誤猜想，得出正確的結論. 教學中教師要充分貫徹“先假設，后驗證”的思路，培養學生的直觀想象、嚴謹推理能力.