數(shù)學(xué)拓展課的教學(xué)策略

陳加倉(cāng)

【摘要】新課改以來(lái)，小學(xué)數(shù)學(xué)拓展性課程越來(lái)越受關(guān)注，小學(xué)數(shù)學(xué)拓展課也應(yīng)運(yùn)而生。很多一線教師也認(rèn)識(shí)到數(shù)學(xué)拓展課的重要性，但是卻不知如何上好這堂課。筆者結(jié)合自己多年來(lái)對(duì)拓展課研究的經(jīng)驗(yàn)，并結(jié)合大量的案例來(lái)分析小學(xué)數(shù)學(xué)拓展課的教學(xué)策略，期望能為一線教師提供切實(shí)可行的小學(xué)數(shù)學(xué)拓展課教學(xué)參考。

【關(guān)鍵詞】拓展課 教學(xué)策略 小學(xué)數(shù)學(xué)

小學(xué)數(shù)學(xué)拓展課是對(duì)小學(xué)數(shù)學(xué)教材進(jìn)行擴(kuò)充、開(kāi)拓、擴(kuò)展、延伸、展開(kāi)的課堂教學(xué)。它的學(xué)習(xí)素材源于教材，寬于教材，又高于教材，并具有豐富性、多樣性和很強(qiáng)的探究性。因此，教師不能簡(jiǎn)單地把它直接呈現(xiàn)給學(xué)生，讓他們“讀”懂;也不能簡(jiǎn)單地靠教師講解與示范，把學(xué)生“講”懂。小學(xué)數(shù)學(xué)拓展課到底應(yīng)該怎樣教呢？筆者根據(jù)自己研究小學(xué)數(shù)學(xué)拓展課的經(jīng)驗(yàn)，提出了以下幾點(diǎn)切實(shí)可行的教學(xué)策略。

一、創(chuàng)設(shè)有效情境，發(fā)展問(wèn)題意識(shí)

問(wèn)題意識(shí)是數(shù)學(xué)學(xué)習(xí)得以有效進(jìn)行的一個(gè)重要因素，若沒(méi)有問(wèn)題，學(xué)生也就沒(méi)有進(jìn)一步探究的欲望。在拓展課中，問(wèn)題驅(qū)動(dòng)探究任務(wù)，問(wèn)題引發(fā)思考深度。因此，拓展課教學(xué)首先要?jiǎng)?chuàng)設(shè)有效的情境，發(fā)展學(xué)生的問(wèn)題意識(shí)，激發(fā)學(xué)生的探究需求。有效的情境必須具備趣味性、挑戰(zhàn)性和思考性。

1.創(chuàng)設(shè)富有趣味性的情境

小學(xué)生喜歡趣味的故事、動(dòng)態(tài)的圖片和游戲。因此，拓展課的情境創(chuàng)設(shè)需符合學(xué)生的心理，將探究的主題融入趣味的故事中或者好玩的游戲中。如“讀‘心數(shù)”一課，課的開(kāi)始教師便和學(xué)生賣起關(guān)子，玩起了游戲：同學(xué)們，知道什么是讀心數(shù)嗎？你心里想好一個(gè)數(shù)，我就能把它猜出來(lái)。想不想試試看？接著呈現(xiàn)四張卡片（如圖1），這里有四張卡片，每張卡片上都有哪些數(shù)？找一個(gè)你喜歡的數(shù)，不需要說(shuō)出來(lái)，只要告訴我哪幾張卡片有這個(gè)數(shù)，我就能猜出這個(gè)數(shù)。

“讀‘心數(shù)”游戲的導(dǎo)入，讓學(xué)生被深深地吸引、折服。師生互玩幾次后，再由同桌兩個(gè)人玩，一人想數(shù)，一人猜數(shù)。從游戲互猜數(shù)到自制游戲卡片，一輪“數(shù)學(xué)王國(guó)”里的探秘活動(dòng)開(kāi)始了，在游戲、操作中，學(xué)生逐步感悟二進(jìn)制。創(chuàng)設(shè)富有趣味性的情境能一下子吸引學(xué)生的眼球，使其快速地投入學(xué)習(xí)中。

2.創(chuàng)設(shè)富有挑戰(zhàn)性的情境

小學(xué)生不僅對(duì)“好玩”的數(shù)學(xué)感興趣，也對(duì)有“挑戰(zhàn)性”的數(shù)學(xué)感興趣。根據(jù)學(xué)生的年齡特征，創(chuàng)設(shè)挑戰(zhàn)性的情境，為學(xué)生創(chuàng)造經(jīng)歷“研究數(shù)學(xué)”的機(jī)會(huì)，同時(shí)也為他們創(chuàng)造表現(xiàn)自我、發(fā)展自我的機(jī)會(huì)，讓學(xué)生在研究中找到自信，并形成“我能夠而且應(yīng)當(dāng)學(xué)會(huì)數(shù)學(xué)地思考”的數(shù)學(xué)觀。如“硬幣的滾動(dòng)圈數(shù)”一課，當(dāng)一個(gè)硬幣不動(dòng)，另一個(gè)硬幣繞著它的外沿滾動(dòng)一圈回到原位，這個(gè)硬幣本身滾動(dòng)了幾圈？全班學(xué)生異口同聲地說(shuō)“1圈”，然而驗(yàn)證的結(jié)果卻是“2圈”。和學(xué)生猜想完全不一致的結(jié)果，無(wú)形中為學(xué)生創(chuàng)設(shè)了富有挑戰(zhàn)性的情境，激發(fā)了學(xué)生的學(xué)習(xí)興趣與強(qiáng)烈的探究欲望。

3.創(chuàng)設(shè)富有思考性的情境

教學(xué)情境是為教學(xué)目標(biāo)服務(wù)的，它的核心目標(biāo)是引起學(xué)生的思考，提高學(xué)習(xí)活動(dòng)的思維含量。因此，創(chuàng)設(shè)的問(wèn)題情境需富有思考性，能為學(xué)生提供思考的空間，引發(fā)學(xué)生廣泛的聯(lián)想。如“三角形的最多個(gè)數(shù)”一課，呈現(xiàn)問(wèn)題：把一個(gè)1000邊形的硬紙板，沿著直直的一條線剪一刀，將它分成了若干個(gè)圖形，其中三角形最多有多少個(gè)？有的學(xué)生猜想最多只能剪1個(gè)三角形，有的猜想最多可能會(huì)有2個(gè)，有的認(rèn)為最多可能會(huì)有3個(gè)……到底幾個(gè)？怎么研究？在熱鬧過(guò)后教師引導(dǎo)學(xué)生靜心思考，得出研究方法：先從最簡(jiǎn)單的多邊形開(kāi)始研究，然后慢慢地增加邊數(shù)，發(fā)現(xiàn)三角形的最多個(gè)數(shù)。這樣的情境導(dǎo)入直奔主題，讓學(xué)生帶著問(wèn)題去思考，簡(jiǎn)潔、有效。

二、定位探究方式，學(xué)會(huì)研究方法

小學(xué)數(shù)學(xué)拓展課的學(xué)習(xí)內(nèi)容與教材相比，更具探索性與挑戰(zhàn)性。因此，教師要設(shè)計(jì)有層次的、適合學(xué)生的探究活動(dòng)。探究活動(dòng)前，教師需認(rèn)真分析學(xué)習(xí)素材特征以及學(xué)生的學(xué)情及認(rèn)知特點(diǎn)，定位契合學(xué)生思維發(fā)展的探究方式。課堂中，教師引導(dǎo)學(xué)生自主探究，學(xué)會(huì)研究的方法，積極參與知識(shí)的形成過(guò)程，感悟數(shù)學(xué)思想方法，提升數(shù)學(xué)素養(yǎng)。

1.“半扶半放”型探究

有些拓展課學(xué)習(xí)素材具有一定難度，涉及一些未學(xué)知識(shí)或數(shù)學(xué)方法，學(xué)生探究起來(lái)有難度，這時(shí)就應(yīng)該采用“半扶半放”型探究。“半扶半放”型探究意味著教師不能當(dāng)“甩手掌柜”，在學(xué)習(xí)關(guān)鍵處需“扶”一下學(xué)生。教師要精心組織、策劃教學(xué)活動(dòng)，重點(diǎn)部分要“把舵”，小結(jié)部分要幫助歸納，有爭(zhēng)議的地方需要闡明正確的觀點(diǎn)。

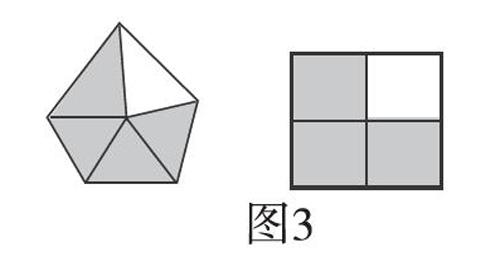
如“老大哥分?jǐn)?shù)”一課。筆者放手讓學(xué)生探究，結(jié)果出現(xiàn)了兩種典型的錯(cuò)誤。錯(cuò)例1用長(zhǎng)方形表示出分?jǐn)?shù)再比較（如圖2），認(rèn)為圖中空白部分都是1份，所以一樣大。錯(cuò)例2用不同的圖表示出分?jǐn)?shù)再比較大小（如圖3），結(jié)果發(fā)現(xiàn)不好比較。此時(shí)，筆者介入并“扶”一下學(xué)生：畫(huà)圖比較兩個(gè)分?jǐn)?shù)的大小時(shí)，首先要畫(huà)完全一樣的圖，接著再對(duì)圖形進(jìn)行平均分并涂出相應(yīng)的份數(shù)，最后比較大小。引導(dǎo)學(xué)生在辨析中理清了比較的前提與方法。

當(dāng)出現(xiàn)“比涂色部分大小”與“比空白部分大小”兩種方法時(shí)，組織學(xué)生比較，然后點(diǎn)撥：更大;比空白部分大小（剪下空白部分重疊在一起，如圖4）， 推理得到更大。前者直接比大小，后者通過(guò)推理比大小，都是好方法。

接著讓學(xué)生比較多個(gè)“老大哥分?jǐn)?shù)”的大小，很快就發(fā)現(xiàn)空白部分越來(lái)越小，涂色部分就越來(lái)越大，“老大哥分?jǐn)?shù)”就越來(lái)越大。

此時(shí)，借助幾何畫(huà)板演示，讓學(xué)生直觀感知“老大哥分?jǐn)?shù)”的分子分母越來(lái)越大，分?jǐn)?shù)也越來(lái)越接近1（如圖5）。同樣的方法延伸至“老二哥分?jǐn)?shù)”（分子比分母小2）……

整個(gè)探究過(guò)程步步為營(yíng)，層層深入，適時(shí)在關(guān)鍵處點(diǎn)撥，讓只學(xué)習(xí)了“分?jǐn)?shù)的初步認(rèn)識(shí)”的學(xué)生，不僅認(rèn)識(shí)了“老大哥分?jǐn)?shù)”，且掌握了真分?jǐn)?shù)的性質(zhì)，有效挖掘了學(xué)生的潛能，發(fā)展了數(shù)感。

2.開(kāi)放型探究

還有一些拓展課學(xué)習(xí)素材基于教材的知識(shí)點(diǎn)，通過(guò)小組合作的方式即可探究學(xué)習(xí)，此類學(xué)習(xí)素材就采用開(kāi)放型探究方式。在開(kāi)放型探究中，雖然學(xué)生不需要“扶”著走路，但在關(guān)鍵處還需教師指引方向。當(dāng)學(xué)生探究進(jìn)入“死角”且長(zhǎng)時(shí)間出不來(lái)時(shí)，教師要引導(dǎo)其“回頭看”;當(dāng)學(xué)生探究走到“十字路口”時(shí)，要引導(dǎo)其“辨方向”;當(dāng)學(xué)生探究路徑不多時(shí)，要引導(dǎo)其“另辟蹊徑”。教師需引導(dǎo)學(xué)生學(xué)會(huì)合作，有時(shí)還需讓學(xué)有余力的學(xué)生離開(kāi)座位幫助不會(huì)的學(xué)生共同完成探究任務(wù)。

如“畫(huà)面積為2cm2的正方形”一課，呈現(xiàn)問(wèn)題：面積是2cm2的正方形，你們會(huì)畫(huà)嗎？學(xué)生通過(guò)計(jì)算找不到兩個(gè)相同的數(shù)的乘積為2，甚至有個(gè)別學(xué)生提出面積為2cm2的正方形不存在。就在學(xué)生的思考進(jìn)入“死角”時(shí)，筆者引導(dǎo)他們“回頭看”：（1）你會(huì)畫(huà)哪些正方形？（2）由邊長(zhǎng)想面積，畫(huà)不出2cm2的正方形，能否直接從面積角度去思考呢？點(diǎn)拔后放手讓學(xué)生自主探究，再匯報(bào)交流。

在交流過(guò)程中教師引導(dǎo)學(xué)生對(duì)這三種方法進(jìn)行比較分析后再激發(fā)學(xué)生繼續(xù)思考，最終學(xué)生的思維被打開(kāi)。肯定了學(xué)生的更多的精彩想法后，引導(dǎo)學(xué)生繼續(xù)思考，學(xué)生又能蹦出新的想法。

在探究之后，筆者引導(dǎo)學(xué)生比較分析，總結(jié)方法：有些是由“大面積”想到“小面積”，有些是由“小面積”想到“大面積”，有些屬于“等積變形”，還有由對(duì)角線長(zhǎng)度想到正方形的面積。通過(guò)比較分析，學(xué)生在反思中進(jìn)一步理清解決問(wèn)題的思路。

三、設(shè)計(jì)分層練習(xí)，提升思維品質(zhì)

練習(xí)是課堂教學(xué)的重要組成部分，是學(xué)生學(xué)習(xí)過(guò)程中不可缺少的重要環(huán)節(jié)。小學(xué)數(shù)學(xué)拓展課也需要設(shè)計(jì)相應(yīng)的練習(xí)，幫助學(xué)生進(jìn)一步掌握知識(shí)，提升思維品質(zhì)。不過(guò)，練習(xí)設(shè)計(jì)要充分考慮學(xué)生之間的差異，讓不同的層次學(xué)生都有機(jī)會(huì)挑戰(zhàn)，獲得成功的體驗(yàn)。

如“涂色問(wèn)題”一課，當(dāng)學(xué)習(xí)了棱長(zhǎng)為n的正方體涂色問(wèn)題之后，筆者設(shè)計(jì)了基礎(chǔ)性練習(xí)、拓展性練習(xí)及非常規(guī)性練習(xí)，幫助學(xué)生進(jìn)一步鞏固知識(shí)，深刻理解知識(shí)。

1.基礎(chǔ)性練習(xí)

（1）將一個(gè)棱長(zhǎng)為5cm的正方體表面涂色，然后切成棱長(zhǎng)為1cm的小正方體，請(qǐng)問(wèn)三面涂色、兩面涂色、一面涂色、沒(méi)有涂色的小正方體各有幾個(gè)？

（2）將長(zhǎng)5cm，寬4cm，高3cm的長(zhǎng)方體表面涂色，然后切成棱長(zhǎng)為1cm的小正方體，請(qǐng)問(wèn)三面涂色、兩面涂色、一面涂色、沒(méi)有涂色的小正方體各有幾個(gè)？

第（1）題是正方體的涂色問(wèn)題，與之前學(xué)習(xí)的內(nèi)容相同;第（2）題是長(zhǎng)方體的涂色問(wèn)題，涂色的小正方體個(gè)數(shù)的計(jì)算方法略有不同，因此，這樣的基礎(chǔ)性練習(xí)既能鞏固知識(shí)，又能“舉一反三”，培養(yǎng)學(xué)生思維的靈活性。

2.拓展性練習(xí)

如圖6，將棱長(zhǎng)4厘米的正方體5個(gè)面涂上顏色，然后切成棱長(zhǎng)1cm的小正方體，請(qǐng)寫(xiě)出小正方體的涂色情況及相應(yīng)的個(gè)數(shù)。

此拓展性練習(xí)緊扣學(xué)習(xí)內(nèi)容，進(jìn)行適當(dāng)?shù)赝卣棺兓＞毩?xí)之后再與6個(gè)面涂色問(wèn)題進(jìn)行對(duì)比，讓學(xué)生充分體會(huì)到各種涂色小正方體的個(gè)數(shù)與位置的變化及原因，讓思考變得更全面，培養(yǎng)學(xué)生思維的縝密性。

3.非常規(guī)性練習(xí)

將36塊相同的小正方體拼成一個(gè)長(zhǎng)方體，表面涂色，然后分開(kāi)，則三面涂色的小正方體最多有多少塊？最少有多少塊？

此題一呈現(xiàn)，學(xué)生會(huì)脫口而出“最多有8塊，最少也有8塊”，因?yàn)槿嫱可男≌襟w在頂點(diǎn)處，且長(zhǎng)方體、正方體都只有8個(gè)頂點(diǎn)。經(jīng)點(diǎn)撥，學(xué)生繼續(xù)思考想象、討論交流，最終分別得到正確答案32塊與0塊。

非常規(guī)性練習(xí)從表面上看似與一般習(xí)題沒(méi)有區(qū)別，但是求解的途徑與思維方式卻完全不同。它能讓學(xué)生在練習(xí)中“恍然大悟”，克服思維定式，促使學(xué)生學(xué)會(huì)更全面地思考問(wèn)題。

當(dāng)然，不是每一節(jié)數(shù)學(xué)拓展課都要設(shè)計(jì)三個(gè)層次的練習(xí)，應(yīng)根據(jù)教學(xué)內(nèi)容、教學(xué)時(shí)間與學(xué)情靈活確定。

四、分類反思概括，培養(yǎng)建模能力

數(shù)學(xué)建模是數(shù)學(xué)知識(shí)與數(shù)學(xué)應(yīng)用的橋梁。研究和學(xué)習(xí)數(shù)學(xué)建模能幫助學(xué)生探索數(shù)學(xué)的應(yīng)用，產(chǎn)生對(duì)數(shù)學(xué)的興趣和應(yīng)用數(shù)學(xué)的意識(shí)和能力。數(shù)學(xué)拓展課中模型的建構(gòu)并非一蹴而就，它滲透在學(xué)生獲得知識(shí)和解決問(wèn)題的過(guò)程中。因此，要引導(dǎo)學(xué)生在觀察實(shí)驗(yàn)、比較分析、抽象概括等活動(dòng)中不斷反思，挖掘背后蘊(yùn)涵的數(shù)學(xué)思想方法，幫助學(xué)生建立數(shù)學(xué)模型，從而達(dá)到解決問(wèn)題的目的。

如“三角形的拼接”一課，這是一節(jié)幾何類拓展課，在教學(xué)中一般讓學(xué)生經(jīng)歷“猜想—驗(yàn)證—發(fā)現(xiàn)”的過(guò)程，體會(huì)方法多樣性以及最優(yōu)化，體驗(yàn)思維的深層次挖掘帶來(lái)的快樂(lè)。課始，教師先呈現(xiàn)問(wèn)題：10個(gè)三角形拼接，有14個(gè)連接點(diǎn)，有幾條邊？學(xué)生無(wú)從下手，教師引導(dǎo)其從2個(gè)、3個(gè)三角形拼接開(kāi)始研究（如圖7）。之后提出猜想：三角形個(gè)數(shù)-1=邊數(shù)-點(diǎn)數(shù);接著引導(dǎo)學(xué)生在5個(gè)、6個(gè)、7個(gè)，甚至更多個(gè)數(shù)的三角形拼接中驗(yàn)證，結(jié)果發(fā)現(xiàn)猜想是正確的;緊接著在n個(gè)三角形拼接的基礎(chǔ)上，再增加一個(gè)三角形拼接，發(fā)現(xiàn)猜想還是正確的。在此基礎(chǔ)上，探究“四邊形的拼接”，發(fā)現(xiàn)同樣的規(guī)律，以此類推到五邊形、六邊形拼接，歸納總結(jié)“多邊形個(gè)數(shù)-1=邊數(shù)-點(diǎn)數(shù)”，最后解釋原因，溝通聯(lián)系，發(fā)現(xiàn)這些多邊形拼接都可轉(zhuǎn)化成三角形的拼接。

此課，讓學(xué)生充分經(jīng)歷探究過(guò)程，在舉例、猜想、驗(yàn)證等活動(dòng)中滲透化歸思想，建立模型并解決問(wèn)題，初步感受數(shù)學(xué)歸納法，培養(yǎng)空間觀念和推理能力。

小學(xué)數(shù)學(xué)拓展課的教學(xué)策略是靈活變化的，應(yīng)該根據(jù)不同的學(xué)習(xí)素材，充分考慮學(xué)情，選擇最適合學(xué)生的學(xué)習(xí)方式，引導(dǎo)學(xué)生探究。