一體兩翼蘊精彩，數形雙飛顯妙趣
——基于知識內涵、思想方法的平面向量解題策略探析

重慶市巴南區西南大學華南城中學 (401346) 夏文濤

《高中數學課程標準》指出向量是近代數學中重要和基本的數學概念之一，它是溝通代數、幾何與三角的一種工具，有著極其豐富的實際背景[1].鑒于此，在全國各地高考數學試卷中，平面向量成為了必考內容，其考查形式靈活多樣，時常出現內容新穎別致的題目，它們在考查基礎知識和基本技能的同時，注重對分析問題和解決問題能力的考查.

向量進入中學數學課程是一個相對緩慢的過程，直達2003年我國頒布《高中數學課程標準》，平面向量才全面進入高中數學.此后初期高考中，平面向量的考查內容主要是向量的基本運算，突出向量代數運算公式的運用.隨著課程改革的推進，平面向量的教學日益深入，平面向量廣泛運用到代數、三角、幾何等領域，這不僅使我們加深了對向量的認識，也拓展了解決代數、三角、幾何問題的思路.與此同時，高考對平面向量的考查也逐漸發生變化,不僅重視對向量的基本運算的考查，還注重對向量的幾何意義、向量應用、向量與其他知識的綜合.對于這些問題的解決，我們運用向量的代數形式居多，特別是向量的坐標方法，因為向量具有完美的運算結構系統，能夠使得問題的解決程序化，也正因如此，我們的向量教學和向量解題更多地圍繞著基本運算公式、運算律而進行.其實，這樣既不利于我們準確把握平面向量的知識內涵，也使得在學習向量的過程中失去了對數學思想方法的領悟.

1.平面向量的知識內涵與數形結合的思想方法

從向量的知識內涵上看，向量是一種具有方向的線段，集數與形為一體，既具有代數形式，又具有幾何特征，即向量是數形的“一體”，而代數形式和幾何特征是向量的“兩翼”.一方面，作為代數的對象，向量可以運算，如向量的加法、減法、數乘、數量積等運算，并且在直角坐標系中存在坐標運算形式；另一方面，作為幾何的對象，向量具有方向、大小，可以刻畫角度、長度、面積、體積等幾何度量問題.

向量內涵上的數與形的特點，也為數形結合思想提供了良好的載體.平面向量的代數運算、幾何意義是向量作為數形結合良好載體的兩大形式，在認識向量時，我們就有了數學思想方法的理論支撐，這也為解決向量問題提供了數學思想方法層面的理論依據.

2.平面向量代數運算和幾何本質的融通性

2.1 向量加法、減法運算的原理是平行四邊形定理

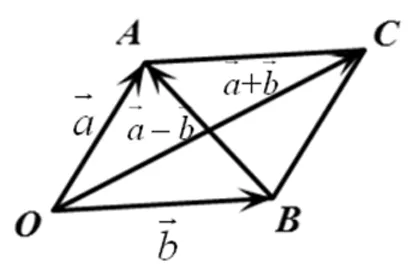
圖1

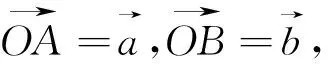
2.2 向量的數乘運算的內涵是線段的伸縮理論

2.3 向量的數量積運算的內涵是余弦定理[5]

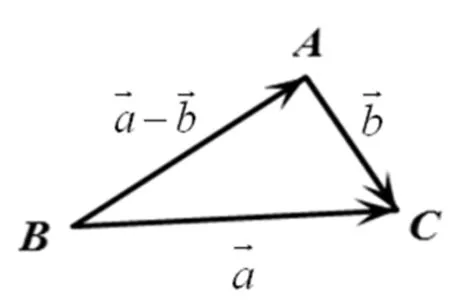
圖2

3.平面向量的解題策略

向量的數形特點溝通了代數和幾何的聯系，打通了向量與代數、幾何、三角交匯的通道，也為高考向量的命題創新奠定了基礎.數學解題策略是最高層次的數學解題方法，是對數學習題途徑的概括性認識.戴再平教授認為就局部范圍內的題目討論，若涉及的知識有限，這個范圍內題目的解題策略的個數將是有限的，我們可能通過逐一考慮這些題目策略，探索一般規律，歸納出一個邏輯化、模式化的方案，從而形成解題策略.[2]羅增儒教授在《數學解題引論》中指出解題策略具有四個基本特征：①普遍的適應性；②直接的可用性；③方法的二重性；④選擇的最優性.[1]

基于以上向量知識內涵和數形結合思想，結合最近幾年高考平面向量部分試題的特點，我們不難總結出滿足以上四個特征的兩大策略：

(1)從向量的代數形式出發，建立直角坐標系或選擇恰當的公式，回歸代數運算；

(2)從向量的幾何意義出發，構造恰當的幾何圖形，轉化為幾何問題.

兩大解題策略，各有優勢，面對一個具體問題，可能要發揮向量的運算優勢解題，而優勢需要透過表象，揭示出問題的幾何本質，以簡化運算.這里，我們根據兩大解題策略，通過對高考平面向量部分試題的分析和研究，總結出平面向量問題解決的基本思路和過程：

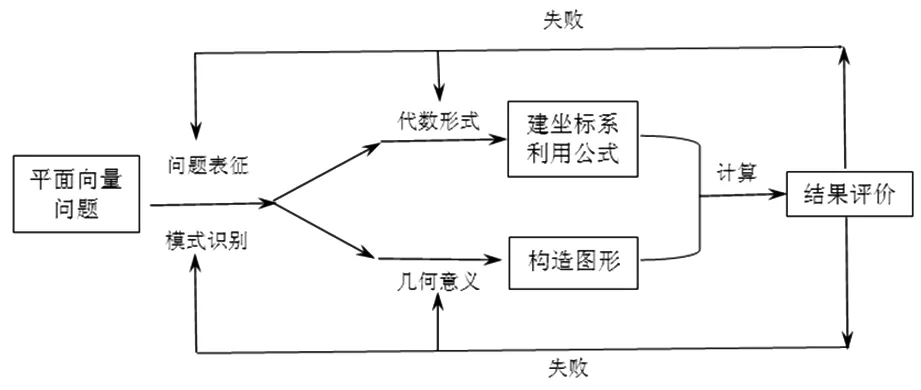
4.典型例題分析

根據以上平面向量解題策略，我們從全國各地的高考數學試題中選擇出部分典型試題，從向量代數形式和幾何意義兩個方面出發，分別探討問題的解決過程，從中體會兩大解題策略的一些特點和規律.

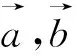
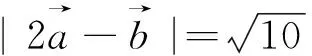
圖3

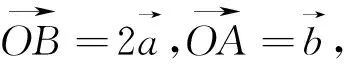
評注:解法1和解法2殊途同歸，特別是①式和②式的相同性，很好地呈現了向量數與形的融通性.

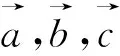
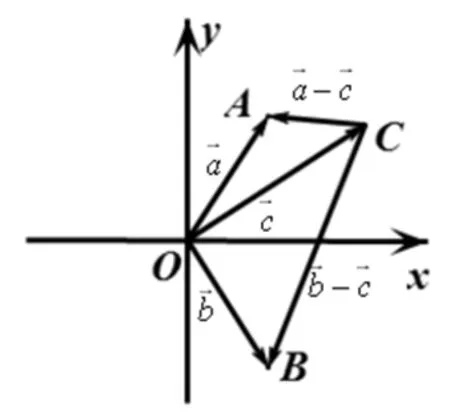
圖4

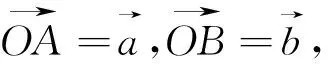
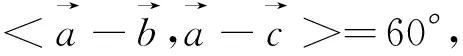
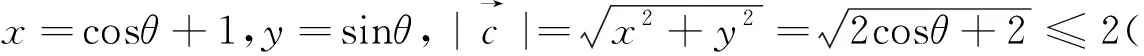
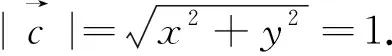
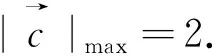
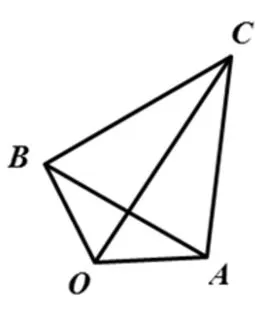
圖5

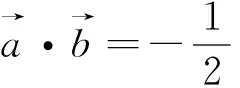
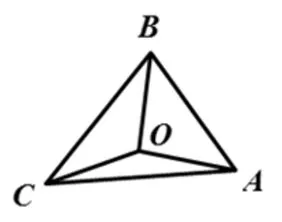
圖6

評注:本題幾何特征色彩重、代數運算難度大，是體現向量幾何意義解題的經典試題.

5.思考與感悟

5.1 向量教學應該保持數形的統一性

數學課程應該返璞歸真，努力揭示數學概念、法則、結論的發展過程和本質.在向量的教學中，我們一直重視向量工具性的價值，側重向量的運算，突出公式的識記，而忽視向量內涵的提煉和升華.例如，從實用的角度出發，利用向量方法去解決幾何、三角函數問題，如此固然可以體現向量的實用功能，但是一味地重復單一的方法，可能會影響學生創新思維的形成、創造能力的發展.

高中數學新課程倡導自主探索的學習方式，力求使學生的學習過程成為教師引導下的“再創造”的過程.向量“一體兩翼”的數形特點，為學生提供了良好的學習探究平臺.對課堂教學來說，以數形的統一性去引導向量教學，不僅有利于學生形成完整性的向量知識，也為向量在解決三角函數、平面幾何等問題提供了知識基礎.另外，數形的統一性也為向量的知識內涵上升到思想方法的高度提供了可能性，這樣通過對向量數形的探索學習，學生通過數學教學獲得的不僅僅是向量的知識內容，也經歷了數形結合思想方法的體驗.

5.2 向量的解題應該堅持策略的選擇性

長期以來，高中數學的解題一直存在著“對題型，套方法”，通過“題海戰術”，猜題押題的現象.對于平面向量，一些教師和學生認為記住公式就行，遇到向量問題就套用公式，或者見到幾何問題，建立直角坐標系，或者解完題后缺乏反思，滿足單一方法，誤以為是“通法”.其實，平面向量具有數形融通性的特征，這既是向量內涵的題中之義，也是數學思想的必然結果.

跳出平面向量解題的單一、僵化的定勢思維，從向量內涵、數形結合的角度審視平面向量，回歸知識本源，體現數學思想，這樣不僅豐富了數學知識，提煉了數學思想，發展數學能力，也不斷提高了數學素養.解題策略的選擇取決于實際解題實踐的需要，解題實踐豐富和發展解題策略，二者的結合是數學解題的內在要求.向量兩大解題策略，各有其優勢，兼具有不足，具體的選擇應根據實際問題的特點而取舍，這樣就超越了解題策略本身，體現了數學解題思維的發散性、靈活性、創新性.